Planung einer Unterrichtseinheit zum Thema Cosinussatz

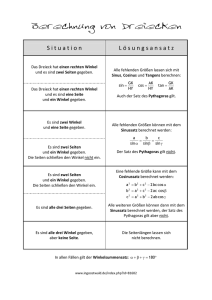
Planung einer Unterrichtseinheit zum Thema Cosinussatz
5. Klasse AHS
Ziel der Stunde: die Schüler sollen Cosinussatz und Sinussatz anwenden können. Sie sollen aus
einer Aufgabenstellung alle nötige Information herauslesen um daraus eine Skizze anfertigen
können, mit deren Hilfe sie die Aufgabe lösen können.
3’
„Guten Morgen“ „Könnt ihr euch noch erinnern, womit wir uns in der letzten Stunde
beschäftigt haben?“
1’
4’
„Wie wird die Länge der Hypothenuse berechnet, wenn man die Kathetenlängen kennt?“ =>
„SvP: Hypothenuse^2 = Kathete1^2 + Kathete2^2“
2’
5’
2’
5’
„Wie kann die Länge der Seite berechnet werden, wenn man Schenkel 1, 2 und den Winkel
kennt? => „Cosinussatz: Seite^2 = Schenkel1^2 + Schenkel2^2 –
2*Schenkel1*Schenkel2*cos(Winkel)“
„Die Formulierung c^2 = a^2 + b^2 – 2a*b*cos(gamma) ist nicht an die Benennung der
Dreiecksseiten gebunden!!“ Sobald man 2 Seiten und den eingeschlossenen Winkel
kennt, kann man die gegenüberliegende Seite berechnen
„Wie wird der Sinussatz formuliert?“ => „a/sin(alpha) = b/sin(beta) = c/sin(gamma)” Auch
hier ist es wichtig, von den Bezeichnungen a, b, c Abstand zu nehmen: Die Verhältnisse
Seite - gegenüberliegender Winkel sind gleich.
Aufgabe 629a: Skizze zeichnen:
„Wie wird der Umfang und der Flächeninhalt eines Parallelogramms berechnet?“
3’
e = 290, f = 238, ε = 71,67°, u = 2*a + 2*b, A = a*h
3’
„Wie können wir a und b berechnen?“ => „Für die Länge a betrachten wir das gelbe Dreieck,
für die Länge b das Grüne.“
5’
2’
Da jeweils 2 Seiten und ein Winkel bekannt sind, kann der Cosinussatz angewendet
werden (unabhängig davon, wie die Seiten und der Winkel benannt sind):
a² = (e/2)² + (f/2)² – 2*(e/2)*(f/2)*cos() => a = 155,99
b² = (e/2)² + (f/2)² – 2*(e/2)*(f/2)*cos(180-) => b = 214,567
U = 2*155,99 + 2*214,567
“Wie kann die Seite h berechnet werden?“ => Sinussatz. Dazu benötigen wir erst den
Winkel 
2’
„Betrachten das blaue Dreieck:“
2’
5’
Mit dem Cosinussatz kann eine Seite eines Dreiecks berechnet werden, wenn die
beiden anderen Seiten sowie der durch die beiden Seiten eingeschlossene Winkel
bekannt ist
e² = a² + b² – 2*a*b*cos()
 = 78,166
3’
„Wie wird nun die Höhe berechnet?“ => Anwendung von Sinus = GK/H
sin() = GK/H = h/b
h = 210
A = 155,99*210 = 32757,9