Matr.-Nr.:

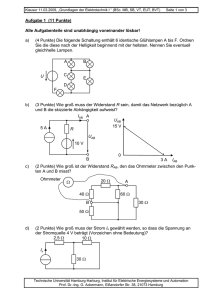
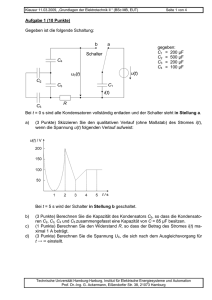
Klausur 18.09.2009, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT)
Seite 1 von 5
Matr.-Nr.:
Aufgabe 1 (6 Punkte)
In der Schaltung sind die beiden Lampen identisch und die Batterie sei eine ideale Spannungsquelle. Der Kondensator ist anfänglich ungeladen. Zum Zeitpunkt t = 0 wird der Schalter geschlossen.
Schalter
UBatterie
A
C
B
a)
Aufgabe
(1 Punkt) Geben Sie die Helligkeit von Lampe A unmittelbar nach Schließen des Schalters an.
Lampe A leuchtet nicht.
Lampe A leuchtet, aber weniger hell als Lampe B.
Lampe A leuchtet gleich hell wie Lampe B.
Lampe A leuchtet heller als Lampe B.
b)
(2 Punkte) Geben Sie die Spannung am Kondensator UC
unmittelbar nach Schließen des Schalters in Abhängigkeit
von der Batteriespannung UBatterie an.
UC = 0
0 < UC < 0,5 · UBatterie
UC = 0,5 · UBatterie
0,5 · UBatterie < UC < UBatterie
UC = UBatterie
c)
(1 Punkt) Geben Sie die Helligkeit von Lampe A eine lange Zeit nach Schließen des Schalters an.
Lampe A leuchtet nicht.
Lampe A leuchtet, aber weniger hell als Lampe B.
Lampe A leuchtet gleich hell wie Lampe B.
Lampe A leuchtet heller als Lampe B.
d)
(2 Punkte) Geben Sie die Spannung am Kondensator UC
eine lange Zeit nach Schließen des Schalters in Abhängigkeit von der Batteriespannung UBatterie an.
UC = 0
0 < UC < 0,5 · UBatterie
UC = 0,5 · UBatterie
0,5 · UBatterie < UC < UBatterie
UC = UBatterie
Antwort (ankreuzen)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 18.09.2009, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT)
Seite 2 von 5
Aufgabe 2 (6 Punkte)
Gegeben ist folgende Schaltung von Kondensatoren:
mit:
C1 = 200 µF
C2 = 50 µF
C3 = 20 µF
C4 = 90 µF
Wges = 86,4 mWs
a)
b)
c)
Aufgabe
(2 Punkte) Fassen sie die Kondensatoren C1 bis C4 zu
C1234 zusammen und berechnen sie die Kapazität.
(2 Punkte) Berechnen sie die Ersatzkapazität C12345 für
die Kondensatoren C1 bis C5. Gehen sie davon aus,
dass bei voller Ladung aller Kondensatoren die Energie
Wges gespeichert ist.
(2 Punkte) Berechnen sie die Kapazität des Kondensators C5.
Antwort
C1234 =
C12345 =
C5 =
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 18.09.2009, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT)
Seite 3 von 5
Aufgabe 3 (9 Punkte)
Der dargestellte Transformator hat folgende Abmessungen:
a = 100 mm
b = 80 mm
A = 600 mm2 (an allen Stellen)
w1 = 1000
µ0 = 0,4 ⋅ π ⋅ 10-6 Vs/Am
µr = 104
Bmax = 1,8 T
Eisenkern
a
b
A
w1 w2
u1(t)
u2(t)
Der Transformator soll eine Wechselspannung u1(t) von 230 V (effektiv) mit 50 Hz in eine
Spannung u2(t) mit etwa 24 V (effektiv) transformieren. Die ohmschen Widerstände der Wicklungen und Streuung sollen für die Rechnungen vernachlässigt werden. Alle möglicherweise
durch den Einschaltvorgang entstandenen Ausgleichsvorgänge seien abgeklungen.
a)
b)
c)
d)
e)
f)
Aufgabe
(1 Punkt) Wie groß ist der magnetische Widerstand des Eisenkreises?
(1 Punkt) Wie groß ist der magnetische Fluss im Eisen für
B = Bmax
(2 Punkte) Wie groß ist der Effektivwert von u1(t), wenn der
Scheitelwert der Flussdichte gleich Bmax ist?
(1 Punkt) Wie groß ist die Selbstinduktivität der Spule 1?
Antwort
(1 Punkt) Wie groß muss w2 gewählte werden (ganzzahlig aufrunden)?
(3 Punkte) Skizzieren Sie zu dem dargestellten Verlauf der
Spannung u1(t) den Verlauf der im Eisenkern gespeicherten
magnetischen Energie und berechnen Sie den maximalen Wert
dieser Energie für U1 = 230 V.
u1(t)
0
10
20 ms
t
10
20 ms
t
Maximalwert =
Wmagn(t)
0
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 18.09.2009, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT)
Seite 4 von 5
Aufgabe 4 (4 Punkte)
Mit der dargestellten Messeinrichtung wird ein unbekannter (Bipolar-) Transistor untersucht.
Die Tabelle zeigt das Ergebnis von sechs Versuchen.
Versuch
a
b
c
d
e
f
a)
b)
Verbindungen
1
2
3
X
Y
X
Y
X
Y
Y
X
Y
X
Y
X
Ergebnis
5kΩ
A
I=0
I≠0
I≠0
I=0
I=0
I=0
I X
T
5V
1
Y
Aufgabe
(2 Punkte) Welcher der Anschlüsse 1, 2 und 3 ist der Anschluss
der Basis.
(2 Punkte) Handelt es sich um einen npn- oder pnp-Transistor?
Begründen Sie Ihre Antwort stichwortartig.
3
2
Antwort
Aufgabe 5 (6 Punkte)
Gegeben ist nun die folgende Schaltung. Für die Transistoren sollen die üblichen Vereinfachungen angenommen werden (IC≈IE; Verstärkung β ≈ B;UBE = 0,6 V).
U2 = 12 V
I1 = 15 mA
IC1 = 0,7 A
R1 = 1 Ω
R2 = 2 Ω
R3 = 3 kΩ
B2 = 90
R1
R3
IC1
IC2
T1
T2
U1
I1
U2
R2
a)
b)
c)
Aufgabe
(1 Punkt) Berechnen Sie den Strom IC2.
(2 Punkte) Wie groß ist die Stromverstärkung B1, des Transistors T1?
(3 Punkte) Wie groß darf U1 maximal sein, damit in T2 die zulässige Verlustleistung von 20 W nicht überschritten wird?
Antwort
IC2 =
B1 =
U1 =
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 18.09.2009, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT)
Seite 5 von 5
Aufgabe 6 (4 Punkte)
Die Abbildung zeigt eine Schaltung mit einem idealen Operationsverstärker.
R3
R1
U1
U2
I4
R1
R2
R4
I3
R2
=
=
=
=
=
=
4V
2V
2 mA
3 kΩ
2 kΩ
0,5 kΩ
I4
U1
a)
b)
c)
U2
Ua
U-
R4
Aufgabe
(1 Punkt) Berechnen Sie den Wert der Spannung U − .
(2 Punkte) Berechnen Sie den Wert des Stromes I3.
(1 Punkt) Die Ausgangsspannung soll Ua = -5 V betragen. Berechnen Sie den Wert des Widerstandes R3.
Antwort
U− =
I3 =
R3 =
Aufgabe 7 (5 Punkte)
Die Abbildung zeigt eine Operationsverstärkerschaltung mit idealem Operationsverstärker
und komplexen Ein- und Ausgangssignalen.
C3
R3
Komplexe Übertragungsfunktion:
U
G(jω) = a = f(R1, R2 , R3, C1, C3 )
Ue
R1
Ue
a)
b)
C1
R2
Aufgabe
(1 Punkt) Wie groß ist die Spannung an C1?
(4 Punkte) Bestimmen Sie die komplexe Übertragungsfunktion G(jω) als Funktion der Größen R1, R2,
R3, C1 und C3.
Ua
Antwort
G(jω) =
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg