C1 C2 C3 C4 U2 U Vorname: Nachname: Matr.-Nr.:

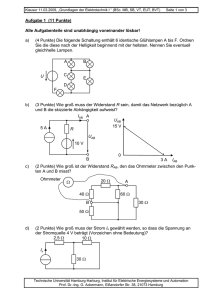
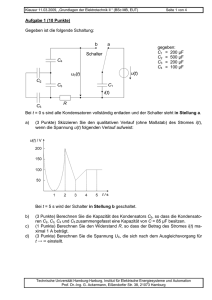
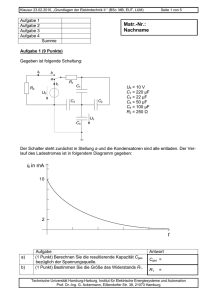
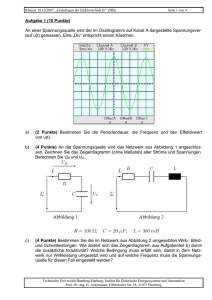
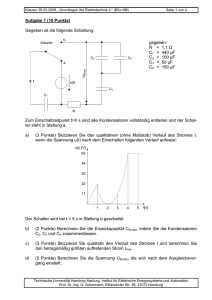
Klausur 15.08.2011 „Grundlagen der Elektrotechnik II“ (MB, EUT, LUM)
Vorname:
Seite 1 von 5
Nachname:
Matr.-Nr.:
Aufgabe 1 (6 Punkte)
Gegeben ist folgende Schaltung aus Kondensatoren. Die Kapazitäten der Kondensatoren
C1, C2 und C3 sind zu C123 zusammengefasst. Die Ladung auf Kondensator C4 ist Q4.
C1
C2
gegeben:
U
= 15 V
C1
= 220 µF
C2
= 22 µF
C123 = 50 µF
= 1,5 ⋅ 10-3 As
Q4
U2
C4
U
C3
Antwort hier eintragen
a)
(1 Punkt) Berechnen Sie die Kapazität des
Kondensators C4.
C4 =
b)
(2 Punkte) Berechnen Sie die Kapazität des
Kondensators C3.
C3 =
c)
(1 Punkt) Berechnen Sie die Ladung des
Kondensators C3.
Q3 =
d)
(1 Punkt) Berechnen Sie die Spannung U2
über dem Kondensator C2.
U2 =
e)
(1 Punkt) Berechnen Sie die in allen Kondensatoren gespeicherte Energie Wges.
Wges =
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 15.08.2011 „Grundlagen der Elektrotechnik II“ (MB, EUT, LUM)
Seite 2 von 5
Aufgabe 2 (5 Punkte)
In der Abbildung sind zwei unendlich lange Leiter (Hin- und Rückleiter), in denen der
Strom I1 = 5 A fließt, dargestellt. Das Magnetfeld soll für den Punkt P untersucht werden.
Hinweis: Es handelt sich um eine maßstabsgetreue Zeichnung.
P
I1
I1
Antwort hier eintragen
a)
(2 Punkte) Zeichnen Sie qualitativ in die Abbildung
die einzelnen Magnetfeldvektoren im Punkt P und
In Abbildung eintragen
beschriften Sie eindeutig.
b)
(1 Punkt) Bestimmen Sie die einzelnen Beträge |H1|
|H1| =
und |H2| der Feldkomponente im Punkt P. Beachten
Sie den Hinweis.
|H2| =
c)
(2 Punkte) Zeichnen Sie den Vektor der resultierenden Magnetfeldkomponente für den Punkt P in die
Abbildung ein und geben Sie den Betrag der Magnet- |Hges| =
feldstärke |Hges| an.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 15.08.2011 „Grundlagen der Elektrotechnik II“ (MB, EUT, LUM)
Seite 3 von 5
Aufgabe 3 (7 Punkte)
Auf dem dargestellten, ringförmigen Eisenkern (kreisförmige Fläche A mit dem
Durchmesser d) ist eine Spule aufgebracht, die über einen Widerstand R1 an eine
Gleichspannungsquelle U1 angeschlossen ist. Vereinfachend soll der ohmsche Widerstand
der Spule sowie Felder außerhalb des Kerns vernachlässigt und der mittlere Weg s zur
Berechnung des magnetischen Widerstandes verwendet werden.
U1
R1
r
d
w
µ0
µr
s
R1
r
I1
U1
w
X
A
=
=
=
=
=
=
=
10 V
5Ω
18 cm
4 cm
80
4 π 10-7 Vs / Am
10000
X
ESB:
X-X
d
A
µr
Antwort hier eintragen
a)
(2 Punkte) Tragen Sie die Richtung des magnetischen Flusses im Eisenkern ein. Skizzieren Sie das
In die Abbildung bzw. in
magnetische Ersatzschaltbild und tragen Sie alle reden Kasten eintragen
levanten Größen sowie Zählpfeile ein.
b)
(3 Punkte) Berechnen Sie die Werte des magnetischen Widerstandes Rmag, der Durchflutung Θ und Rmag =
des magnetischen Flusses Ф.
Θ=
Ф=
c)
(2 Punkte) Wie groß ist die im Kern gespeicherte
magnetische Energie W?
W=
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 15.08.2011 „Grundlagen der Elektrotechnik II“ (MB, EUT, LUM)
Seite 4 von 5
Aufgabe 4 (7 Punkte)
Die dargestellte Schaltung soll die Helligkeit der Lampe H steuern.
UV
UE
IL
UL
R1
H
UV
UE
=
24 V
= 0,5 V… 4 V
verstellbar
Transistor:
B > 50
UBE = 0,7 V (für IB > 0)
UCE = 0,7 V (für B ⋅ IB > IC)
weiterhin gelten die üblichen Vereinfachungen.
Lampe H:
UL,nenn =
24 V = UV
Nennspannung
IL,nenn =
2A
Nennstrom
2
⎛ I ⎞
UL = U V ⋅ ⎜⎜⎜ L ⎟⎟⎟
(nur für Aufgabe c)
⎜⎝ IL,nenn ⎠⎟
Rkalt =
0,25 Ω
(nur für Aufgabe d)
Antwort hier eintragen
a)
(2 Punkte) Berechnen Sie R1 so, dass die Lampe für
UE = 4 V auf jeden Fall mit ihrem Nennstrom versorgt
R1 =
wird.
b)
(1 Punkt) Für welchen Bereich der Spannung UE ist
der Lampenstrom IL null?
c)
< UE <
(2 Punkte) Die Helligkeit der Lampe kann durch UE
eingestellt werden. Ermitteln Sie die in dem Transistor
in Wärme umgesetzte Verlustleistung PV in Abhängigkeit von UV und IL. (UCE und UL dürfen in der FunkPV =
tion nicht vorkommen.)
Die durch den Basisstrom erzeugte Leistung kann
vernachlässigt werden.
d)
(2 Punkte) In kaltem Zustand hat die Lampe den angegebenen Widerstand Rkalt. Die Spannung UE wird
sprungartig von 0 V auf 4 V erhöht. Im ersten Moment
I =
nach dem Sprung ist die Lampe noch kalt. Wie groß L
ist der Strom IL unmittelbar nach dem Sprung?
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 15.08.2011 „Grundlagen der Elektrotechnik II“ (MB, EUT, LUM)
Seite 5 von 5
Aufgabe 5 (8 Punkte)
Gegeben ist folgendes Netzwerk. Alle Bauteile werden als ideal betrachtet. Der Widerstand R5 kann im Bereich von 0 bis 5 kΩ variiert werden. Dabei gilt zu jedem Zeitpunkt die
Beziehung R4 + R5 = 5 kΩ.
R3
R1
Gegeben:
R2
-
R2
R3
U1
UZ
+
U1
R4
UZ
= 1 kΩ
= 1 kΩ
= 15 V
= 10 V
UA
U5
R5
Antwort hier eintragen
a)
b)
(2 Punkte) Berechnen Sie UA in Abhängigkeit von U5
und UZ.
(2 Punkte) Wie groß ist UA für R5 = 0,5 kΩ?
UA =
UA =
c)
(2 Punkte) Welchen Wert darf R1 maximal annehmen,
wenn der Strom durch die Zener-Diode für den oben
angegebenen Bereich von R5 mindestens 4 mA R1,max =
betragen soll?
d)
(2 Punkte) Für welchen Wert von R5 (bei R1 = R1,max
R5 =
aus Aufgabenteil c)) ist die Verlustleistung PZ in der
Zener-Diode am größten und wie groß ist sie?
PZ,max =
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg