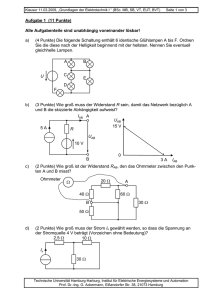
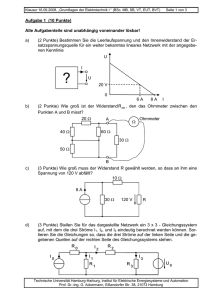
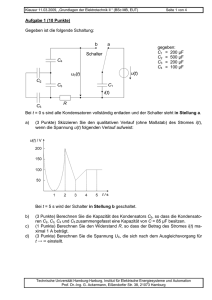
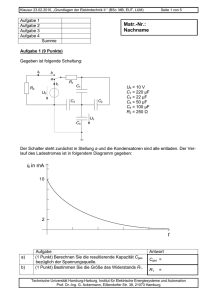
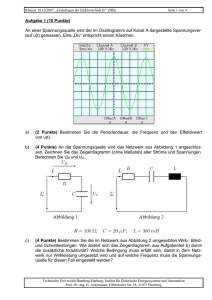
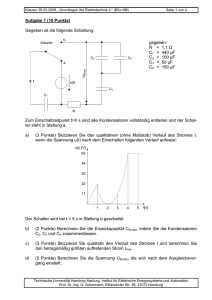
(*)

Klausur 23.02.2010, „Grundlagen der Elektrotechnik I “ (BSc. MB, SB, VT, EUT, BVT, LUM)
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Aufgabe 5
Aufgabe 6
Seite 1 von 6
Matr.-Nr.:
Nachname:
Summe
Aufgabe 1 (5 Punkte)
Drei identische Glühlampen sind wie im Schaltbild rechts dargestellt über einen Widerstand an eine Spannungsquelle angeschlossen. Die Widerstände der Verbindungsdrähte sind
vernachlässigbar gering. Der Verlauf der Strom-SpannungsKennlinie der Lampen ist unbekannt.
Ri
A
U
Messungen der Ströme durch die Lampen mit einem als ideal
zu betrachtenden Amperemeter ergeben die Werte IB = 0,3 A
und IC = 0,5 A durch Lampe B bzw. C.
a)
Aufgabe
(2 Punkte) Für die an Lampe A anliegende Spannung gilt im
Vergleich zur Spannung an Lampe C:
− UA < 0,5 · UC
− UA = 0,5 · UC
− UA > 0,5 · UC und UA < UC
− UA = UC
− UA > UC
C
B
Antwort (ankreuzen)
(nur eine Antwort richtig)
Begründen Sie kurz Ihre Antwort:
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 23.02.2010, „Grundlagen der Elektrotechnik I “ (BSc. MB, SB, VT, EUT, BVT, LUM)
b)
(1 Punkt) Für den durch Lampe A fließenden Strom folgt
aus den gegebenen Messwerten:
Seite 2 von 6
(nur eine Antwort richtig)
−
−
−
−
IA = 0,2 A
IA = 0,3 A
IA = 0,5 A
Der Strom durch Lampe A beträgt mehr als 0,3 A
jedoch nicht notwendigerweise 0,5 A.
− Es lässt sich keine Aussage über den Strom
durch Lampe A treffen.
Begründen Sie kurz Ihre Antwort:
c)
(2 Punkte) Betrachten Sie die folgenden beiden Aussagen:
Aussage A: Es kann entschieden werden, ob Ri = 0 oder Ri > 0 ist.
Aussage B: Die Kennlinie der Glühlampen ist nicht linear (d. h. Strom und Spannung
sind nicht proportional).
Welche der Aussagen lassen sich aus den Angaben schließen?
−
−
−
−
Nur Aussage A
Nur Aussage B
Aussage A und Aussage B
Keine der beiden Aussagen
Begründen Sie kurz:
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 23.02.2010, „Grundlagen der Elektrotechnik I “ (BSc. MB, SB, VT, EUT, BVT, LUM)
Seite 3 von 6
Aufgabe 2 (5 Punkte)
Gegeben ist folgendes Netzwerk:
Aufgabe
Antwort
a)
(1 Punkt) Berechnen Sie IY.
b)
(1 Punkt) Berechnen Sie UX.
c)
(2 Punkte) Wie groß muss der Widerstand R gewählt werden, damit über der Stromquelle eine Spannung von 210 V R =
abfällt?
(1 Punkt) Welche Leistung wird in dem 40 Ω Widerstand
P=
umgesetzt?
d)
IY =
UX =
Aufgabe 3 (3 Punkte)
Das folgende Netzwerk weist an den Klemmen A und B die skizzierte Abhängigkeit auf. Für
die Widerstände R0 und R gilt: R = 5R0
Aufgabe
a)
(1 Punkt) Berechnen Sie den Strom I0.
b)
(2 Punkte) Berechnen Sie die Widerstände R0 und R.
Antwort
I0 =
R0 =
R =
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 23.02.2010, „Grundlagen der Elektrotechnik I “ (BSc. MB, SB, VT, EUT, BVT, LUM)
Aufgabe 4 (4 Punkte)
Die Schaltung rechts enthält eine ideale Wechselspannungsquelle u0(t) mit u0(t)= Û0 ⋅ cos (ωt+φ0), zwei Widerstände R1
und R2, sowie eine Induktivität L. Die Größe i0(t) bezeichnet
den durch die Spannungsquelle fließenden Strom, uL, uR1, iL
und iR1 die Spannungen und Ströme an den mit den Indices
bezeichneten Elementen.
Tritt in den nachfolgenden Teilaufgaben zwischen den jeweils
genannten Signalen eine Phasenverschiebung auf oder haben die beiden Signale die gleiche Phase (gleiche Phase:
Phasendifferenz = 0° oder 180°)?
a)
Aufgabe
(2 Punkte) uL(t) und uR1(t)
uR1(t) und u0(t)
iL(t) und iR1(t)
i0(t) und u0(t)
b)
(2 Punkte) In der obigen Schaltung wird nun der
Widerstand R2 überbrückt. Ändert sich dadurch…
− der Effektivwert des Stromes iR1(t)?
− die auf u0(t) bezogene Phase des Stromes
iR1(t)?
Seite 4 von 6
R1
i0(t)
u0(t)
L
R2
Antwort
… Phasenverschiebung
… gleiche Phase
… Phasenverschiebung
… gleiche Phase
… Phasenverschiebung
… gleiche Phase
… Phasenverschiebung
… gleiche Phase
… Ja
… Ja
… Nein
… Nein
Begründen Sie jeweils kurz Ihre Antwort.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 23.02.2010, „Grundlagen der Elektrotechnik I “ (BSc. MB, SB, VT, EUT, BVT, LUM)
Seite 5 von 6
Aufgabe 5 (12 Punkte)
Das gezeigte Netzwerk wird mit der Wechselspannung U versorgt. Die gegebenen Parameter sind:
U
= 40 V · ej0˚
f
= 50 Hz
|ZR| = 20 Ω
I1
U
C1
I2
R
|ZC1| = 15 Ω
|ZL| = 30 Ω
|ZC2| = 10 Ω
a)
b)
L
Aufgabe
(2 Punkte) Zeichnen Sie ein qualitatives Zeigerbild
(ohne Maßstab) der Größen I1, U C1, U L und U und
tragen Sie die zugehörigen Zählpfeile in die Darstellung des Netzwerkes ein:
(2 Punkte) Zeichnen Sie ein qualitatives Zeigerbild
(ohne Maßstab) der Größen I2, U C2, U R und U
und tragen Sie die zugehörigen Zählpfeile in die
Darstellung des Netzwerkes ein:
C2
Antwort
in Kasten
in Kasten
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 23.02.2010, „Grundlagen der Elektrotechnik I “ (BSc. MB, SB, VT, EUT, BVT, LUM)
c)
d)
(1 Punkt) Berechnen Sie den Strom I1. Geben Sie
das Ergebnis in Exponentialform an.
(1 Punkt) Berechnen Sie den Strom I2. Geben Sie
das Ergebnis in Exponentialform an:
Seite 6 von 6
I1 =
I2 =
Falls Sie keine Lösung in c) ermittelt haben, verwenden Sie für die folgenden Aufgabenteile:
I1 = 2,5 A · e-j90° und I2 = 1,6 A · ej30°
e)
f)
g)
(1 Punkt) Berechnen Sie die von der Spannungsquelle abgegebene Wirkleistung
(2 Punkt) Berechnen Sie die von der Spannungsquelle abgegebene Blindleistung (nur Betrag).
(3 Punkte) Berechnen Sie L so, dass der Spannungsquelle keine Blindleistung abgefordert wird.
P =
Q=
L =
Aufgabe 6 (9 Punkte)
Drehstromnetz 400 V, 50 Hz
QN
QV
IN
IV I
A
C1 C2 C3
Verbraucher A
100 kW, cos ϕ = 0,3
IB
Verbraucher B
200 kW, cos ϕ = 0,9
An ein Drehstromnetz sind zwei Verbraucher A und B mit den angegebenen Daten angeschlossen. Die Leistungsfaktoren cos ϕ sind für beide Verbraucher induktiv.
a)
Aufgabe
(1 Punkt) Wie groß sind die Ströme IA und IB?
Antwort
IA =
IB =
b)
c)
d)
e)
(3 Punkte) Wie groß ist der Strom IV in der Zuleitung
zu beiden Verbrauchern (möglicherweise ist ein
kleines Zeigerbild für die Ströme und Spannungen in
Leiter 1 hilfreich)?
(1 Punkt) Wie groß ist die Blindleistung QV, die beide Verbraucher gemeinsam aufnehmen?
(2 Punkte) Wie groß müssen die Kompensationskondensatoren C1, C2 und C3, (C1 = C2 = C3) gewählt werden, damit QN = 0 ist? (Angabe in F, mF,
µF o. ä.)
(2 Punkte) Wie groß ist der Strom IN für den Fall,
dass der Verbraucher B ausgeschaltet ist?
.
IV =
QV =
C1 = C2 = C3 =
IN =
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg