Aufgabe 1 (9 Punkte) Gegeben ist die folgende Schaltung: C2 = 200
Werbung

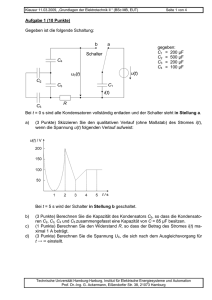
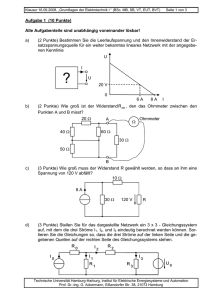
Klausur 16.09.2008, „Grundlagen der Elektrotechnik II “ (BSc MB, EUT) Seite 1 von 3 Aufgabe 1 (9 Punkte) Gegeben ist die folgende Schaltung: C2 C1 U U3 C3 C4 C2 C3 C4 Q1 U = = = = = 200 µF 15 µF 5 µF 1,2⋅10-3 As 24 V a) (1 Punkt) Berechnen Sie die Kapazität des Kondensators C1. b) (2 Punkte)Fassen Sie die Kondensatoren C2, C3 und C4 zu einer Ersatzkapazität C234 zusammen. c) (2 Punkte) Berechnen Sie die Ladung Q2 des Kondensators C2. d) (2 Punkte) Berechnen Sie die Spannung U3 am Kondensator C3. e) (2 Punkte) Wie groß ist die Energie, die insgesamt in allen Kondensatoren gespeichert ist? Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg Klausur 16.09.2008, „Grundlagen der Elektrotechnik II “ (BSc MB, EUT) Seite 2 von 3 Aufgabe 2 (11 Punkte) Aufgabe 2 A In der nebenstehenden Skizze ist ein Pendel dargestellt, an dessen Ende sich ein mit N („Nordpol“) und S („Südpol“) bezeichneter hufeisenartiger Permanentmagnet befindet. Im Luftspalt des Magneten befindet sich eine Spule A, deren Enden herausgeführt sind und die Messung der induzierten Spannung u(t) ermöglicht. Wenn das Pendel in Ruhe ist, befindet sich die Spule wie dargestellt symmetrisch im Luftspalt. Das Pendel wird nun zu Schwingungen etwa mit der dargestellten Amplitude angestoßen. Der Winkel α ändert sich mit der Zeit etwa sinusförmig mit der Eigenfrequenz des Pendels. Es wird eine Spannung induziert, wenn sich der Permanentmagnet in der Nähe der Spule befindet, etwa ab dem durch „Grenze für Induktion“ markierten Abstand. a) α N A S u(t) A (5 Punkte) Skizzieren Sie α(t) und u(t) für etwa eine Pendelperiode über einer gemeinsamen Zeitachse t. Über den Wickelsinn der Spule ist nichts bekannt, Sie können also das Vorzeichen für u(t) frei wählen. Markieren Sie bei u(t) deutlich die Punkte für α = 0. ΦK d) (2 Punkte) Geben Sie die Zählpfeile und die Größen für die beiden dargestellten Quellen an. (2 Punkte) Berechnen Sie die Selbstinduktivität der Spule 1 Eisen, µr >> 1 I1 Rm,K repräsentiert den gesamten Eisenkreis, Rm,S1 und Rm,S2 repräsentieren Streuflüsse. c) Grenze für Induktion Ansicht a - b Aufgabe 2 B In der nebenstehenden Skizze ist ein Eisenkern mit zwei Spulen 1 und 2 sowie ein zugehöriges elektrisches Ersatzschaltbild dargestellt. b) b a A I2 n1 n2 „1“ „2“ Rm,K Rm,S1 ΦK Rm,S2 (2 Punkte) Berechnen Sie die Gegeninduktivität zwischen beiden Spulen (Vorzeichen ist ohne Belang) Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg Klausur 16.09.2008, „Grundlagen der Elektrotechnik II “ (BSc MB, EUT) Seite 3 von 3 Aufgabe 3 (9 Punkte) Gegeben ist folgende Schaltung. Für die Transistoren sollen die üblichen Vereinfachungen angenommen werden ( IC ≈ IE ; Verstärkung β ≈ B = 50; UBE = 0,6 V (const); IB ist so klein, dass R, 3R als unbelasteter Spannungsteiler aufzufassen ist). Zahlenwerte: = 20 V U1 =2V U2 R =1Ω =4A I1 =2A IL a) b) R 3R IL IC (2 Punkte) Wie groß sind die Ströme IC und IB? IB U1 T (4 Punkte) Wie groß ist die Spannung UCE ? UCE RL 0,25 R R c) I1 (3 Punkte) Wie groß ist die in der Last RL umgesetzte Leistung? Aufgabe 4 (11 Punkte) Ie R2 IB R3 Uz = 300 µA, = 10 kΩ, = 20 µA, = 100 kΩ R2 Der Operationsverstärker sei als ideal angenommen. Die Zener-Diode sei ideal (UD = 0) mit der Zener-Spannung Ie R3 Uz = 4,7 V Ua IB a) (5 Punkte) Die Zener-Diode sei nicht vorhanden. Geben Sie dafür die Ausgangsspannung Ua in Abhängigkeit von den Größen Ie, R2, IB, und R3 an und berechnen Sie den Zahlenwert. b) (6 Punkte) Skizzieren Sie (für den Fall mit Zener-Diode) das Diagramm Ua = f(Ie) für -500 µA ≤ Ie ≤ 1000 µA. Alle anderen Größen sind wie oben angegeben. Berechnen Sie den Strom Ie für die markanten Punkte im Verlauf der Funktion. Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg