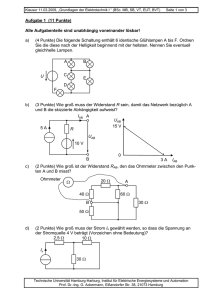
Aufgabe 1 (10 Punkte) Gegeben ist die folgende Schaltung: Bei t = 0

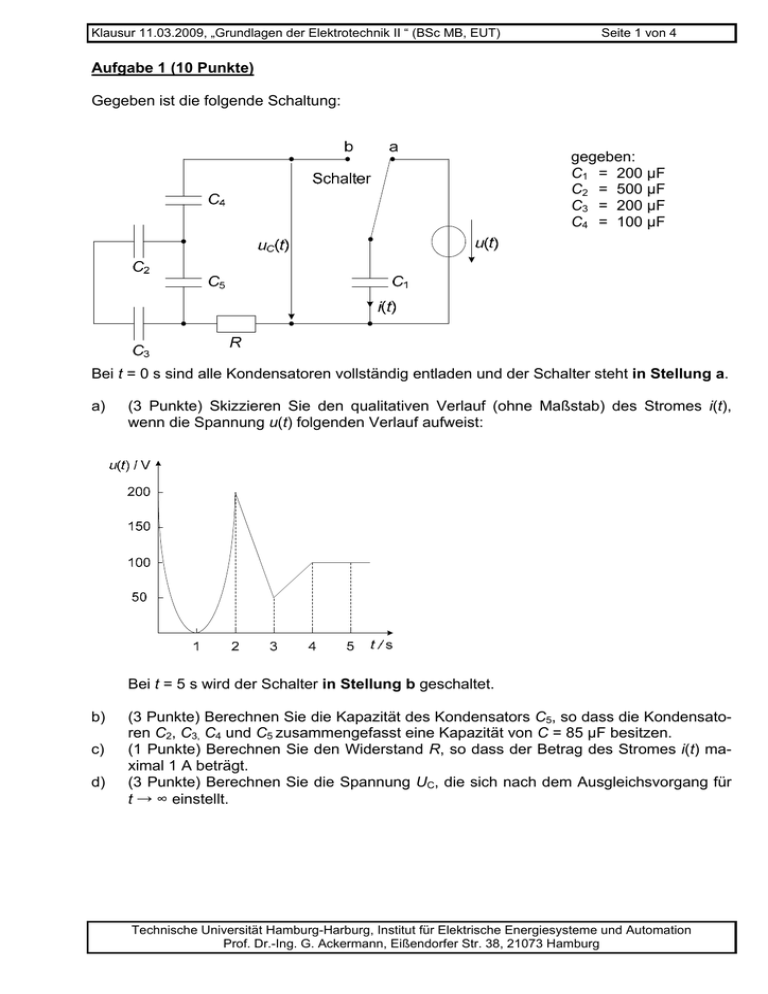
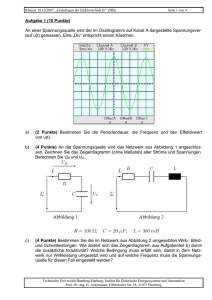
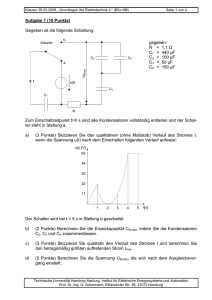
Klausur 11.03.2009, „Grundlagen der Elektrotechnik II “ (BSc MB, EUT)
Seite 1 von 4
Aufgabe 1 (10 Punkte)
Gegeben ist die folgende Schaltung:
gegeben:
C1 = 200 µF
C2 = 500 µF
C3 = 200 µF
C4 = 100 µF
Bei t = 0 s sind alle Kondensatoren vollständig entladen und der Schalter steht in Stellung a.
a)
(3 Punkte) Skizzieren Sie den qualitativen Verlauf (ohne Maßstab) des Stromes i(t),
wenn die Spannung u(t) folgenden Verlauf aufweist:
Bei t = 5 s wird der Schalter in Stellung b geschaltet.
b)
c)
d)
(3 Punkte) Berechnen Sie die Kapazität des Kondensators C5, so dass die Kondensatoren C2, C3, C4 und C5 zusammengefasst eine Kapazität von C = 85 µF besitzen.
(1 Punkte) Berechnen Sie den Widerstand R, so dass der Betrag des Stromes i(t) maximal 1 A beträgt.
(3 Punkte) Berechnen Sie die Spannung UC, die sich nach dem Ausgleichsvorgang für
t → ∞ einstellt.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 11.03.2009, „Grundlagen der Elektrotechnik II “ (BSc MB, EUT)
Seite 2 von 4
Aufgabe 2 (10 Punkte)
Es soll eine Induktivität von 200 mH entsprechend
der dargestellten Skizze gebaut werden. Für den
Ringkern aus Eisen gibt der Hersteller an:
Rm = 50000 A/Vs
A = 1 cm2
magnetischen Widerstand
Eisenquerschnitt
A
mittlerer Umfang (Weglänge der
= 15 cm
Feldlinien)
(Das Feld im Kern sei homogen, Streuung sei vernachlässigbar.)
i
Eisenkern
u(t)
A
Umax u(t)
t
-Umax
0 1 2 3 4 5 6 7 ms
a)
(2 Punkte) Welche Windungszahl ist erforderlich?
b)
(2 Punkte) Wie groß darf der Strom in der Spule maximal sein, damit die magnetische
Flussdichte im Kern den Wert von 0,8 T nicht überschreitet?
c)
(3 Punkte) Wie groß darf die Spannung Umax des dargestellten rechteckförmigen Spannungsverlaufes maximal sein, damit die magnetische Flussdichte den in b) angegebenen Wert nicht überschreitet? (Für t < 0 sei der Strom null.)
d)
(3 Punkte) Skizzieren Sie (ohne Maßstab an der vertikalen Achse) zu dem angegebenen Spannungsverlauf den Verlauf der im Kern gespeicherten magnetischen Energie
und berechnen Sie den maximalen Wert. (Für t < 0 sei der Strom null.)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 11.03.2009, „Grundlagen der Elektrotechnik II “ (BSc MB, EUT)
Seite 3 von 4
Aufgabe 3 (10 Punkte)
a) (4 Punkte) Mit der dargestellten Messeinrichtung wird ein unbekannter (Bipolar-) Transistor untersucht. Die Tabelle zeigt das Ergebnis von sechs Versuchen. Welcher der
Anschlüsse 1, 2 und 3 ist der Anschluss zur Basis des Transistors und handelt es sich
um einen npn-oder pnp-Transistor? Begründen Sie Ihre Antwort stichwortartig.
Versuch
Verbindungen
1
2
X
Y
X
X
Y
X
Y
Y
a
b
c
d
e
f
5kΩ
A
Ergebnis
3
I=0
I=0
I=0
I=0
I>0
I>0
Y
Y
X
X
I X
T
1
5V
Y
3
2
Gegeben ist nun die folgende Schaltung. Für die Transistoren sollen die üblichen Vereinfachungen angenommen werden (IC ≈ IE; Verstärkung β ≈ B; UBE = 0,6 V).
R3
IC1
T1
IC2
T2
R2
U1
I1
U2
R1
Zahlenwerte: U1 = 20 V, U2 = 10 V, I1 = 10 mA, R1 = 2 Ω, R2 = 1 kΩ, R3 = 4 Ω, B = 90
b)
(1 Punkt) Berechnen Sie den Strom IC1.
c)
(2 Punkte) Berechnen Sie den Strom IC2.
d)
(3 Punkte) Berechnen Sie die Verlustleistungen der Transistoren PV1 und PV2. (Verluste
durch die Basisströme vernachlässigbar.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 11.03.2009, „Grundlagen der Elektrotechnik II “ (BSc MB, EUT)
Seite 4 von 4
Aufgabe 4 (10 Punkte)
Die Abbildung zeigt eine Schaltung mit einem idealen Operationsverstärker und einer idealen
Diode.
S
R1
D
R3
R2
OP
U1
U2
R1 = 1 kΩ
R2 = 1 kΩ
R3 = 2 kΩ
U3
Ua
U1 = 5 V
U2 = 4 V
U3 = 3 V
a)
(4 Punkte) Berechnen Sie die Spannung Ua bei geöffneten Schalter S.
b)
(6 Punkte) Der Schalter S wird geschlossen.
Die Spannung U2 sei nun variabel im Intervall von -3 V bis +3 V einstellbar.
Skizzieren Sie den Verlauf der Spannung Ua als Funktion der Spannung U2.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg