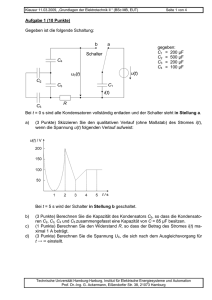
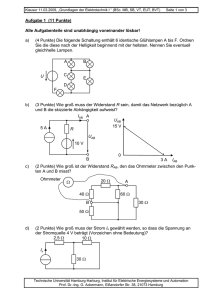
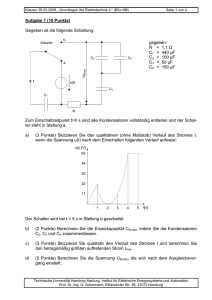
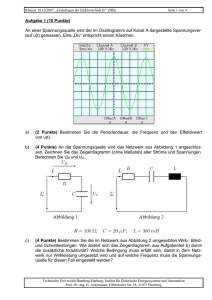
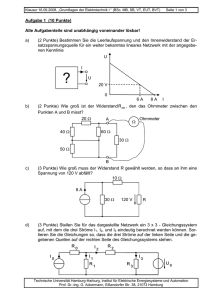
(*)

Klausur 23.02.2010, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT, LUM)
Aufgabe 1
Aufgabe 2
Aufgabe 3
Aufgabe 4
Seite 1 von 5
Matr.-Nr.:
Nachname
Summe
Aufgabe 1 (9 Punkte)
Gegeben ist folgende Schaltung:
U0 = 10 V
C1 = 220 µF
C2 = 22 µF
C3 = 50 µF
C4 = 100 µF
R2 = 250 Ω
Der Schalter steht zunächst in Stellung a und die Kondensatoren sind alle entladen. Der Verlauf des Ladestromes ist in folgendem Diagramm gegeben:
a)
b)
Aufgabe
(1 Punkt) Berechnen Sie die resultierende Kapazität Cges
bezüglich der Spannungsquelle.
(1 Punkt) Bestimmen Sie die Größe des Widerstands R1.
Antwort
Cges =
R1
=
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 23.02.2010, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT, LUM)
c)
d)
(1 Punkt) Berechnen Sie die gesamte nach unendlich
langer Zeit in den Kondensatoren gespeicherte Ladung
Qges.
(2 Punkte) Berechnen Sie die Spannung U3 über dem
Kondensator C3.
Seite 2 von 5
Qges =
U3
=
Der Schalter wird nach sehr langer Zeit in Stellung b geschaltet.
e)
f)
Aufgabe
(2 Punkte) Berechnen Sie den Strom ib, der unmittelbar
nach dem Umschalten fließt.
(2 Punkte) Tragen Sie den Verlauf des Stromes ib in das
nachfolgende Diagramm ein und vervollständigen Sie die
Achsenbeschriftung der vertikalen Achse.
Antwort
ib =
in Diagramm
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 23.02.2010, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT, LUM)
Seite 3 von 5
Aufgabe 2 (10 Punkte)
a
b
A
w2
µ0
µr
Bmax
R
U1
Eisen= 50 mm
kern
= 40 mm
I1
= 150 mm2 (an allen Stellen)
= 100
U1
= 0,4 ⋅ π ⋅ 10-6 Vs/Am
= 104
= 1,8 T
= 30 Ω
= Wechselspannung 230 V (eff.), 50 Hz
b
a
S
A
I2
w1 w2
U2
R
Der dargestellte Transformator soll die angegebene Wechselspannung in eine kleinere
Spannung transformieren. Die ohmschen Widerstände der Wicklungen und Streuung sollen
für die Rechnungen vernachlässigt werden. Alle möglicherweise durch den Einschaltvorgang
entstandenen Ausgleichsvorgänge seien abgeklungen.
Aufgabe
a)
c)
(2 Punkte) Wie groß muss w1 gewählt werden, damit die angegebene maximale Flussdichte Bmax gerade erreicht wird. (Aufrunden auf ganzzahligen Wert)?
(1 Punkt) Wie groß ist der magnetische Widerstand des Eisenkreises?
(2 Punkte) Wie groß ist für I2 = 0 der Strom I1?
d)
(1 Punkt) Wie groß ist U2 (für I2=0)?
e)
(2 Punkte) Wie groß ist die Gegeninduktivität zwischen den
beiden Wicklungen (ohne Vorzeichen)?
(2 Punkte) Der Schalter S sei geschlossen. Wie groß ist dafür
I1? (Vergessen Sie Ihr Ergebnis aus c) nicht!)
b)
f)
Antwort
(Ströme und
Spannungen als
Effektivwerte!)
w1 =
Rm =
I1
=
U2 =
M12 =
I1
=
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 23.02.2010, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT, LUM)
Seite 4 von 5
Aufgabe 3 (8 Punkte)
Das Netzwerk beinhaltet zwei npn-Bipolartransistoren. Für die Berechnung soll von den üblichen Vereinfachungen ausgegangen werden.
R1
C1
IC2
IB1 B1
I2
C2
B2
UBE1
UV
UCE2
E1
R2
UBE2
E2
RE
Gegeben:
UBE1
UBE2
B1
B2
RL
= 0,4 V
= 0,6 V
= 100
= 200
= 50 Ω
IC2
UCE2
UV
I2
= 10 mA
=5V
= 10 V
= 10 · IB1
a)
Aufgabe
(2 Punkte) Berechnen Sie den Widerstand RE.
b)
(1 Punkt) Berechnen Sie den Strom IB1.
c)
(2 Punkt) Berechnen Sie den Widerstand R2.
d)
(1 Punkt) Berechnen Sie den Widerstand R1.
e)
(2 Punkte) Berechnen Sie die Verlustleistung PV1
des Transistors 1 ohne Basisverluste
Antwort
RE
=
IB1
=
R2
=
R1
=
PV1 =
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Klausur 23.02.2010, „Grundlagen der Elektrotechnik II “ (BSc. MB, EUT, LUM)
Seite 5 von 5
Aufgabe 4 (10 Punkte)
Die Abbildung zeigt eine Schaltung mit zwei idealen Operationsverstärkern und einer idealen
Zenerdiode.
R4
I1
R2
R1
OP 1
U2
OP 2
I3
U1
Uz
R1 = 0,3 kΩ
R2 = 1,0 kΩ
R3 = 0,5 kΩ
R4 = 1,5 kΩ
R5 = 0,8 kΩ
I3 = 3,0 mA
R3
Ua
R5
U1 = 15 V
Uz = 4,7 V
a)
Aufgabe
(2 Punkte) Berechnen Sie den Wert des Stromes I1.
b)
(3 Punkte) Bestimmen Sie den Wert der Spannung U2.
c)
(3 Punkte) Berechnen Sie den Wert der Spannung Ua.
d)
(2 Punkte) Welche Leistung wird im Widerstand R5 umgesetzt?
Antwort
I1 =
U2 =
Ua =
P5 =
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg