algebraische Geometrie - Mathematikinformation

Christina Birkenhake
Algebraische Geometrie - Ein Einblick
Die algebraische Geometrie ist eine faszinierende mathematische Disziplin. Da sie auf zahlreiche, erst
im Hauptstudium gelehrte mathematische Gebiete aufbaut, gilt sie als äußerst schwierige und allenfalls
nur für wenige Experten zugängliche mathematische Disziplin.
In diesem Artikel soll ein Versuch gemacht werden, einen kleinen möglichst anschaulichen Einblick in
diese Materie zu vermitteln. Der Artikel erhebt keinerlei Anspruch auf Vollständigkeit. Für ein weiteres
Studium der Inhalte sowie für die exakten Voraussetzungen der vorgestellten Sätze verweise ich auf die
weitergehende Literatur, einige Standardwerke findet man in den Literaturhinweisen.
Der Name algebraische Geometrie besagt, dass mit algebraischen Methoden Geometrie gemacht wird.
Wir müssen also erst einmal grob klären, was Algebra und Geometrie bedeuten. Beide Begriffe sind aus
der Schulmathematik bekannt.
Die Algebra lässt sich recht einfach charakterisieren: Hier werden algebraische Gleichungen (also Polynomgleichungen) untersucht. Die Grundaufgabe der Algebra lautet: Lösen dieser algebraischen Gleichungen. Nun, das lernt man ja schon in der Schule: Die Lösungen von linearen bzw. quadratischen
Gleichungen sind gerade die Nullstellen der entsprechenden linearen bzw. quadratischen Funktionen.
In Spezialfällen findet man mit der Schulmathematik auch die Lösungen (Nullstellen) von Gleichungen
höheren Grades.
In der algebraischen Geometrie werden dagegen algebraische Gleichungen als algebraische Räume, also
als Kurven, Flächen etc., betrachtet. Damit kommen wir zu dem zweiten Begriff, der Geometrie.
Wir alle haben eine Vorstellung von Geometrie, da Geometrie ja zum Schulstoff gehört. In der Schule
wird euklidische Geometrie gelehrt. Hier untersucht man verschiedenste geometrische Figuren und lernt,
deren Flächen bzw. Volumina zu berechnen. Aber auch das xy-Koordinatensystem, in dem Graphen von
Funktionen dargestellt werden, ist ein Modell der euklidischen Geometrie. Die euklidische Geometrie
wird in der Schule als Modell des uns umgebenden Raumes dargestellt.
Der Alltag lehrt uns aber, dass die euklidische Geometrie nicht ausreicht, unsere Welt zu beschreiben.
Nur ein Beispiel: Längen- und Breitengrade sind jedem Schüler z. B. aus dem Erdkundeunterricht oder
vom Blick auf das GPS im Auto der Eltern bekannt. Hierbei handelt es sich um ein Koordinatensystem
der zweidimensionalen sphärischen Geometrie. Dass es auf einer Kugeloberfläche Zweiecke, Dreiecke etc.
gibt, und dass es die sphärische Trigonometrie gibt, um diese zu berechnen, ist leider ”kein Bestandteil
heutiger mathematischer Schul- und Allgemeinbildung mehr” (vgl. [SS] p.253). Dies soll nur ein kleiner
Hinweis darauf sein, dass es außer der euklidischen Geometrie noch viele weitere Geometrien gibt.
Für die algebraische Geometrie stellt die projektive Geometrie den zweckmäßigen Rahmen dar. Man
könnte sie sozusagen die Mutterdisziplin aller klassischen Geometrien nennen (vgl. [SS] p.445).
Der vorliegende Artikel versucht, anhand von ebenen algebraischen Kurven, insbesondere der elliptischen Kurven, einige Methoden der algebraischen Geometrie anschaulich zu erklären. Dazu werden in
Abschnitt 1 der reelle projektive Raum, Kegelschnitte und ebene Quadriken erklärt. Dieses sollte für
interessierte Schüler der Sekundarstufe II verständlich sein. Abschnitt 2 diskutiert den komplexen projektiven Raum und verschiedene Aspekte der elliptischen Kurven auf anschaulichem Niveau. Der dritte
Abschnitt schließlich stellt einige klassische Sätze der Geometrie algebraischer Kurven und abelsche
Varietäten für den tiefer interessierten Leser vor.
Ab Abschnitt 2.5 werden vermehrt Begriffe aus der komplexen Analysis und der algebraischen Geometrie
verwendet, die nicht alle an dieser Stelle erklärt werden sollen oder können. Die Definition oder Erklärung
vieler dieser Begriffe ist aber für ein Verständnis des gesamten Textes nicht immer nötig. Begriffe oder
Abschnitte, die in diesem Sinne einfach überlesen werden können, werden mit (zwVnn) ( = zum weiteren
Verständnis nicht nötig) gekennzeichnet.
4
1. Kegelschnitte
1.1 Der reelle projektive Raum
Aus der Schule sind der ein-, zwei- und dreidimensionale euklidische Raum bekannt: die reelle Zahlengerade, auch mit R bezeichnet, die xy-Koordinatenebene R2 und das dreidimensionale xyz-Koordinatensystem
als Modell für R3 :
y
x
y
x
x
z
R
R2
R3
Die Elemente dieser Räume sind im eindimensionalen Fall Zahlen x ∈ R, Zahlenpaare oder Punkte
(x|y) ∈ R2 bzw. Zahlentripel oder Punkte (x|y|z) ∈ R3 . Im Folgenden werden wir statt (x|y) bzw.
(x|y|z) die Notation (x, y) bzw. (x, y, z) verwenden.
Die Idee des projektiven Raumes ist eng verbunden mit der Idee der Perspektive und Zentralprojektion. Die Perspektive wurde erst in der Renaissance entwickelt - erstaunlich spät, wenn man bedenkt,
dass unsere optische Wahrnehmung vielmehr der Zentralperspektive als der Euklidischen Geometrie
entspricht.
Jeder Punkt, den wir sehen, entspricht einem Sehstrahl. Da
y
wir nicht nach hinten schauen können, repräsentiert dieser
Sehstrahl (bzw. Punkt) eine Gerade durch unser Auge. Um
dieses mathematisch zu beschreiben, stellen wir uns ein xyzKoordinatensystem, dessen Ursprung in unserem Auge liegt,
vor. Nun sind die Punkte dieses neuen Raumes die Geraden
durch den Ursprung (Auge).
Bekanntlich sieht man mit einem Auge nur zweidimensional.
x
Der oben beschriebene Raum ist dementsprechend ebenfalls
zweidimensional: der zweidimensionale projektive Raum, auch
z
projektive Ebene genannt. Sie wird mit P2 abgekürzt, das
Mengen-P steht für projektiv und der Exponent gibt die Dimension an. Es gilt also:
P2 = Geraden durch 0 in R3 .
Projektive Räume gibt es in jeder Dimension, allgemein definiert man den n-dimensionalen projektiven
Raum als:
Pn = Geraden durch 0 in Rn+1 .
Die Elemente eines projektiven Raumes sind Geraden durch den Nullpunkt, kurz Ursprungsgeraden.
Das ist natürlich gewöhnungsbedürftig. Wir sind es gewohnt, dass Elemente von geometrischen Räumen
Punkte sind. Deswegen spricht man auch bei Elementen projektiver Räume von Punkten (obwohl sie ja
eigentlich Geraden sind).
Um dieses besser zu verstehen, betrachten wir zunächst den
y
eindimensionalen projektiven Raum, auch projektive Gerade
(x 2 ,y2)
genannt. P1 ist nach Definition die Menge aller Ursprungsgeraden der euklidischen Ebene R2 . Was lehrt die Schulmathematik
Δy
über Geraden durch (0, 0) in R2 ? Jede solche Gerade (ausge(x 1 ,y1)
nommen der y-Achse) hat eine Gleichung der Form y = mx mit
∆y
−y1
Δx
der Steigung m = xy22 −x
= ∆x
. Umgekehrt, jede Zahl m ∈ R
1
legt eine Ursprungsgerade, nämlich die Gerade y = mx, fest.
Aus der Zahl m ∈ R wird somit ein Punkt (genauer die Gex
rade y = mx) auf der projektiven Gerade P1 . Auf diese Weise
kann man sich die reelle Zahlengerade R als Teilmenge der
projektiven Gerade P1 vorstellen.
5
Mathematiker sagen dazu, die Zuordnung R 3 m nach {y = mx} ∈ P1 definiert eine Einbettung
R ,→ P1 ,
m=
∆y
∆x
7→ Gerade y = mx.
(1)
Bemerkung 1. Eine Einbettung ist eine injektive Abbildung, d. h. zu jedem Wert gehört genau ein
Urbild. Einbettungen werden durch den Zuordnungspfeil ,→ gekennzeichnet.
y
Was ist nun mit der y-Achse? Hier gibt es keine Steigung der
∆y
1
Form m = xy22 −y
−x1 = ∆x , denn ∆x wäre gleich 0 und man darf
ja nicht durch 0 teilen. Nähern sich die Geraden aber der yAchse an, werden also immer steiler wie in der nebenstehenden
Graphik, so wird ihre Steigung immer größer und im Grenzwert (auch das kennen wir aus der Schule) wird die Steigung
unendlich:
∆y
=∞
my-Achse = lim ∆x
x
∆x→0
Wenden wir uns wieder der Einbettung R ,→ P1 zu, so sehen wir, dass das Bild von R in P1 (also die
Wertemenge) alle Punkte des P1 erfasst bis auf den einen Punkt, der der y-Achse mit der Steigung ∞
entspricht. Damit gilt mengentheoretisch, dass
R ∪ {∞} = P1 .
Das lässt sich nun wieder sehr gut anschaulich vorstellen: Gleich einem Maßband, das die reelle Zahlengerade darstellt, ist so die projektive Gerade das an beiden Enden zusammengeklebte Maßband und ∞
ist der Klebepunkt:
m=1
m=1
m=-1
m=-1
R
m=0
8
m=0
⇒
{∞} ∪ R = P1
In diesem Bild ist P1 eine geschlossene Kurve, hat also keinen Anfang und kein Ende. Mathematiker
sagen dazu: Die projektive Gerade P1 ist kompakt.“ Analoges gilt übrigens für alle projektiven Räume.
”
Wenden wir uns nun dem zweidimensionalen Fall zu: Die projektive Ebene P2 ist als Menge der Geraden durch den Ursprung im Raum R3 definiert. Das ist am Anfang schwer begreiflich. Stellen wir uns dazu eine beliebig aufgestellte Leinwand in R3 vor, d. h. die Leinwand darf nicht den Ursprung
enthalten. Stellen wir uns diese Leinwand als die reelle Ebene R2 , also unendlich ausgedehnt, vor. So schneiden, wie nebenstehend dargestellt, fast alle Urprungsgeraden diese Ebene R2 in genau einem Punkt. In der zweiten nebenstehenden
Graphik ist zusätzlich die zur ersten Leinwand parallele Ebene durch Null eingezeichnet. Die Ursprungsgeraden in dieser
Ebene schneiden die erste Leinwand nicht. Die Gesamtheit der
Ursprungsgeraden in der zweiten Ebene ist wie zuvor als ein
R2
1
eindimensionaler projektiver Raum P zu interpretieren. Somit kann man sich den zweidimensionalen projektiven Raum
P1
P2 (also die Menge der Ursprungsgeraden in R3 ) als reelle Ebene R2 (nämlich die Schnittpunkte der Ursprungsgeraden mit
der ersten Leinwand) zusammen mit einer projektiven Gerade
P1 vorstellen. Diese projektive Gerade wird in diesem Zusammenhang die ∞-ferne Gerade genannt.
P1 ∪ R2 = P2
P2
6
1.2 Homogene Koordinaten
Wie rechnet man mit Punkten in projektiven Räumen? Dazu braucht man homogene Koordinaten, die
in diesem Abschnitt erklärt werden sollen.
Beginnen wir mit den homogenen Koordinaten des P1 . Die allgemeine Geradengleichung in R2 lautet
Ax + By = C, mit A, B, C ∈ R. Bei einer Ursprungsgeraden, also einer Geraden durch den Nullpunkt,
muss C = 0 gelten. Durch Umstellen und Umbenennen der Koeffizienten (a = B, b = −A) erhalten wir
die Gleichung
ay = bx,
(2)
wobei entweder a 6= 0 oder b 6= 0. Jede Ursprungsgerade, also jeder Punkt des P1 , kann so beschrieben
werden. Dabei sind die beiden Koeffizienten a und b aber nicht eindeutig, sie können mit jeder reellen
Zahl α 6= 0 multipliziert werden, denn die Gleichung αay = αbx beschreibt die gleiche Gerade. Eine
Kurzschreibweise für diesen Sachverhalt bieten die homogenen Koordinaten, mit einem Doppelpunkt
getrennte Zahlenpaare:
ay = bx ↔ (a : b) ∈ P1
(3)
Der Doppelpunkt bedeutet, dass mit einer beliebigen Zahl α 6= 0 multipliziert werden darf:
(a : b) = (α a : α b)
(4)
In dieser Terminologie lässt sich auch die Einbettung (1) beschreiben. Die Gerade ay = bx hat, falls
a 6= 0, die Steigung may=bx = ab und somit gilt:
R
may=bx =
b
a
,→
P1
7→
(a : b) = (1 : ab ) = (1 : may=bx )
Jetzt können wir die Geradengleichung (2) und die Koeffizienten a und b zur Seite legen und, wenn wir
nur mit den folgenden Größen arbeiten, wird es übersichtlicher: Eine Zahl m ∈ R wird auf den Punkt
X1
(1 : m) ∈ P1 abbgebildet, umgekehrt entspricht der Punkt (X0 : X1 ) ∈ P1 der Zahl X
∈ R, falls X0 6= 0.
0
Ist aber X0 = 0, so gilt nach der Regel (4), dass (0 : X1 ) = (0 : 1) und dieser Punkt entspricht dem
Punkt ∞:
'
R ∪ {∞}
P1
R3m
↔
(1 : m) ∈ P1
X1
X0
←
(X0 : X1 )
∞
↔
(0 : 1)
Die homogenen Koordinaten des P2 werden analog definiert. Ein beliebiger Punkt von P2 wird dargestellt
durch:
(x0 : x1 : x2 ) = (α x0 : α x1 : α x2 ) ∈ P2 ,
und
2
ne
er
e
ad
:x
1
er
G
:x
)
2
Üblicherweise wird die projektive Ebene durch die nebenstehende Graphik skizziert. Die horizontale Achse entspricht der x-Achse des R2 ⊂ P2 und wird durch die
Gleichung {x2 = 0} beschrieben, die vertikale Achse entspricht der y-Achse und hat die Gleichung {x1 = 0}. Diese beiden Achsen schneiden sich im Punkt (1 : 0 : 0), dem
Bild des Ursprungs (0, 0) von R2 . Die ∞-ferne Gerade hat
(0
P ,→ P , (X0 : X1 ) 7→ (0 : X0 : X1 ).
-f
1
8
R2 ,→ P2 , (x, y) 7→ (1 : x : y),
( x0 : 0 : x 2 )
wobei wieder x0 , x1 und x2 nicht gleichzeitig null sein dürfen, das Tripel (x0 : x1 : x2 ) aber mit jeder
reellen Zahl α 6= 0 multipliziert werden darf. Wir verwenden für die homogenen Koordinaten den P2
Kleinbuchstaben, um sie nicht mit den homogenen Koordinaten des P1 zu verwechseln.
♜
Den Sachverhalt P1 ∪ R2 ' P2 kann man folgendermaßen wiedererkennen: Die Teilmengen R2 und die ∞-ferne ♘ (0:0:1)
Gerade P1 sind die Bilder (also Wertemengen) der Einbettungen
(0:1:0)
♔ (1:0:0)
♖
( x0 : x 1 : 0 )
♞
♚
7
hier die Gleichung {x0 = 0}. Als Geraden in P2 sind die x- bzw. die y-Achse selbst wieder projektive
Geraden und sind je durch einen ∞-fernen Punkt geschlossen. Der ∞-ferne Punkt der x-Achse ist der
Punkt (0 : 1 : 0), derjenige der y-Achse ist (0 : 0 : 1). Als Punkte im Unendlichen müssen diese
beiden Punkte auf der ∞-fernen Geraden liegen, diese ist deswegen in der Graphik als die Gerade
durch diese beiden Punkte skizziert. Leider spiegelt die Graphik nicht die Tatsache wider, dass die drei
Koordinatenachsen jeweils geschlossen sind. Deswegen wurden hier die beiden Enden jeder Geraden
je mit einem weißen bzw. schwarzen Schachsymbol gekennzeichnet. Die Geraden muss man sich an
gleichen Symbolen, jeweils schwarz mit weiß, verklebt denken. Würde man in dieser Graphik die Enden
der Geraden verbinden, so erhielte man weitere Schnittpunkte.
Diese Problematik wird klarer bei der Betrachtung der beiden nachfolgenden Photos, die ein Modell der
reellen projektiven Ebene, aus zwei Perspektiven aufgenommen, zeigen.
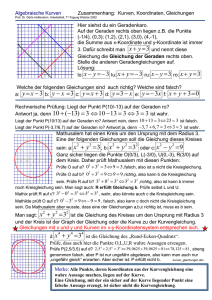
Aufgabe 1.2.1:
Zeige, dass parallele Geraden in R2 einen gemeinsamen Fernpunkt haben.
Aufgabe 1.2.2:
Zeige, dass sich zwei verschiedene Geraden in P2 genau in einem Punkt schneiden.
Aufgabe 1.2.3:
a b mit Determinante ad − bc 6= 0 definiert eine sogenannte Projektivität
Eine 2 × 2-Matrix
c d
P = ac db : P1 7→ P1 , die auf den homogenen Koordinaten durch Multiplikation wirkt:
0
aX0 +cX1
Da ac db X
gilt
P (X0 : X1 ) = (aX0 + cX1 : bX0 + dX1 ).
X1 = bX0 +dX1 ,
Finde die Projektivitäten, die die rationalen Funktionen a) x 7→ x + c, b) x 7→ c · x,
x
fortsetzen.
c) x 7→ − x1 , d) x 7→ 1 + x1 und e) x 7→ x−1
Aufgabe 1.2.4:
Ein Fixpunkt einer Projektivität P : P1 7→ P1 ist ein Punkt p mit P (p) = p.
2
a) Bestimme die Fixpunkte von P = 12 −1
.
b) Zeige, dass eine nicht triviale Projektivität, also P 6= 10 01 , höchstens zwei Fixpunkte
haben kann.
c) Finde eine Projektivität des P1 mit Fixpunkt (1 : −1), welche die Punkte (0 : −1) und
(2 : 0) vertauscht.
8
Aufgabe 1.2.5:
Für Punkte A = (a0 : a1 : a2 ), B = (b0 : b1 : b2 ) und C = (c0 : c1 : c2 ) ∈ P2 sind äquivalent:
i) A, B und C sind kollinear.
ii) Die Geraden GA : a0 xx + a1 x1 + a2 x2 = 0, GB : b0 xx + b1 x1 + b2 x2 = 0 und
GC : c0 xx + c1 x1 + c2 x2 = 0 schneiden sich in einem Punkt.
a0 a1 a2 iii) det b0 b1 b2 = 0
c0 c1 c2
Aufgabe 1.2.6:
Zwei Punkte a, b ∈ Rn (hier können wir einfach n = 1 oder 2 annehmen, es geht aber auch
allgemeiner) definieren eine Gerade G := ab in R2 . Ein Punkt x auf dieser Geraden lässt sich
folgendermaßen schreiben
x = a + t(b − a) = (1 − t)a + tb
mit einem eindeutig bestimmten t ∈ R.
Das Teilverhältnis von x bezüglich a und b ist definiert durch
T V (x ; a, b) :=
t
.
t−1
Falls t = 1 oder äquivalent x = b, so definiert man T V (b ; a, b) = ∞.
a) Bezeichne mit ∞G den ∞-fernen Punkt der Geraden G. Zeige, dass sich T V zu einer
Bijektion T V : G ∪ {∞G } → P1 fortsetzen lässt.
b) Zeige, dass
T V (b ; a, x) = 1 − T V (x ; a, b) ,
T V (a ; b, x) = 1 −
1
,
T V (x ; a, b)
1
,
T V (x ; a, b)
T V (x ; a, b)
T V (a ; x, b) =
.
T V (x ; a, b) − 1
T V (x ; b, a) =
c) Zeige, dass für drei paarweise verschiedene Punkte x, a, b ∈ R gilt
T V (x ; a, b) · T V (a ; b, x) · T V (b ; x, a) = −1 .
d) Zeige, dass für vier paarweise verschiedene Punkte x, a, b, c ∈ R gilt
T V (x ; a, b) · T V (x ; b, c) · T V (x ; c, a) = 1 .
1.3 Kegelschnitte
Die allgemeine quadratische Funktion lautet:
f (x) = ax2 + bx + c
mit reellen Zahlen a 6= 0, b und c. Aus der Schule ist bekannt, dass der Graph von f eine Parabel in R2
ist, die die x-Achse keinmal, einmal oder zweimal schneidet. In der algebraischen Geometrie betrachtet
man statt der Funktion f (x) = ax2 + bx + c die algebraische Gleichung in den zwei Variablen x und y
y = ax2 + bx + c.
(5)
Statt des Graphen von f betrachtet man des Weiteren die so genannte affine algebraische Kurve von
(5) in R2 :
(x, y) ∈ R2 y = ax2 + bx + c .
(6)
9
Nun wird mittels der Einbettung R2 ,→ P2 mit:
R2 3 (x, y) = xx10 , xx20 7→ (1 : x : y) = 1 :
x1
x0
:
x2
x0
= (x0 : x1 : x2 ) ∈ P2
die algebraische Kurve (6) als Kurve im projektiven Raum P2 angesehen und möglicherweise mit ∞fernen Punkten vervollständigt. Man sagt dazu, die Kurve wird in P2 eingebettet bzw. man betrachtet
ihren projektiven Abschluss. Dazu homogenisieren wir die Gleichung (5); wir setzen x = xx10 und y = xx20
und multiplizieren mit x20 , um die Nenner zu entfernen:
x0 x2 = ax21 + bx0 x1 + cx20
(7)
Diese Gleichung ist nun homogen, dass heißt, jedes Monom (also jeder Summand) hat denselben Grad.
Erfüllt ein Punkt (x0 , x1 , x2 ) ∈ R3 die Gleichung (7), so auch jedes Vielfache (α x0 , α x1 , α x2 ). Damit
macht es Sinn zu sagen, dass der Punkt (x0 : x1 : x2 ) ∈ P2 die Gleichung erfüllt. Also beschreibt (7)
eine projektive algebraische Kurve in P2 :
(x0 : x1 : x2 ) ∈ P2 x0 x2 = ax21 + bx0 x1 + cx20
Da die Gleichung (7) vom Grad zwei ist, wird die Gleichung, aber auch die projektive Kurve selber,
Quadrik genannt. Im Fall der Normalparabel f (x) = x2 erhält man auf diese Weise die homogene
Gleichung
x0 x2 = x21
(8)
und die zugehörigen Kurven in R2 und P2 sehen ungefähr so aus:
e
ad
:x
1
er
:x
eG
n
er
)
2
affine Parabel in R
-f
(0, 0)
(0
y
8
( x0 : 0 : x 2 )
(0:0:1)
( x0 : x 1 : 0 )
x
2
(0:1:0)
(1:0:0)
projektive Kurve in P2
Da, wie oben erwähnt, das Modell des P2 fehlerhaft ist, erscheint hier der projektive Abschluss der Normalparabel verzerrt. Deshalb gibt uns dieses Bild nicht Aufschluss über die Form der projektiven Kurve
sondern nur über die Schnittpunkte mit der ∞-fernen Gerade. Diese berechnet man durch Einsetzen
der Gleichung {x0 = 0} in die Gleichung x0 x2 = x21 . So erhält man die Gleichung
0 = x21 .
Das bedeutet, dass die ∞-ferne Gerade die projektive Kurve x0 x2 = x21 genau im Punkt (0 : 0 : 1)
schneidet. Da aber die Gleichung 0 = x21 quadratisch ist, ist die Gerade {x0 = 0} Tangente an die Kurve
in (0 : 0 : 1) und der Schnitt hat die Vielfachheit 2.
Die affine Parabel wurde hier also durch Hinzufügen des ∞-fernen Punktes (0 : 0 : 1) projektiv abgeschlossen. Besonders fällt auf, dass die projektive Kurve x0 x2 = x21 geschlossen, also kompakt ist. Das
gilt für alle projektiven Kurven.
Ein weiterer Vorteil der algebraisch-geometrischen Vorgehensweise ist, dass man auch Kurven betrachten
kann, die zu keinen Funktionen gehören, also nicht in der Form y = f (x) mit einer Funktion f geschrieben
werden können. Um bei den Kegelschnitten zu bleiben, betrachten wir dazu nun das Beispiel der Ellipse.
Die affine bzw. die homogene Gleichung lautet:
affine Gleichung:
x2
y2
+
= 1,
a2
b2
homogene Gleichung:
x21
x22
+
= x20
a2
b2
10
Die zur homogenen Gleichung gehörige projektive Kurve schneidet die ∞-ferne Gerade {x0 = 0} nicht
(siehe Aufgabe 1.3.7). Der Grund dafür ist natürlich, dass die Ellipse schon in R2 geschlossen und
vollständig sichtbar ist:
8
( x0 : 0 : x 2 )
(0:0:1)
-f
:x
e
ad
er )
G
ne : x 2
er
(0
1
y
( x0 : x 1 : 0 )
(0, 0)
(0:1:0)
(1:0:0)
x
projektive Kurve in P2
affine Ellipse in R2
Um die Liste der nicht ausgearteten Kegelschnitte vollständig zu machen, wenden wir uns nun den
Hyperbeln zu. In der Schule lernen wir die Hyperbeln als Graphen der gebrochen rationalen Funktion
f (x) = x1 kennen. Die entsprechende affine bzw. homogene Gleichung lautet:
affine Gleichung: y =
1
,
x
homogene Gleichung:
x2
x0
=
⇔ x1 x2 = x20
x0
x1
An der äquivalenten zweiten Darstellung der homogenen Gleichung erkennen wir, dass es sich hier, wie
bei der Parabel und Ellipse, wieder um eine quadratische Gleichung (Quadrik) handelt. Die affine Kurve
ist bekannt, das Bild der projektiven Kurve könnte in unserem Modell der projektiven Ebene ungefähr
so aussehen:
♜
er
:x
e
ad
er )
G
ne : x 2
1
affine Hyperbel in R2
♔
(0
(0, 0)
x
-f
y
8
( x0 : 0 : x 2 )
(0:0:1)
(0:1:0)
(1:0:0)
( x0 : x 1 : 0 )
♚
♖
projektive Kurve in P2
Rechnerisch (siehe Aufgabe 1.3.7), aber auch in der Graphik, erkennt man, dass die projektive Hyperbel
die ∞-ferne Gerade {x0 = 0} in den beiden Punkten (0 : 0 : 1) und (0 : 1 : 0) schneidet.
Warum erscheint sie nun nicht geschlossen wie die projektiven Kurven zuvor? Das liegt wieder an der
Fehlerhaftigkeit des Modells der projektiven Ebene. Wie am Ende von Abschnitt 1.2 erklärt, sind die
Koordinatenachsen als Geraden in P2 geschlossene Kurven. Ebenso muss man sich die Hyperbeläste
miteinander verklebt denken, jeweils sind schwarze und weiße Symbole zu verbinden.
11
8
( x0 : 0 : x 2 )
(0:0:1)
-f
ne
er
(0
e
ad
:x
1
er
G
:x
)
2
Eine andere Möglichkeit ist, die Ansicht soweit zu verschieben
und zu verzerren, dass der linke Hyperbelast nicht mehr links,
sondern auf der anderen Seite sichtbar wird. Wie das aussehen
könnte, wird in der nebenstehenden Graphik gezeigt.
Zusammenfassend sehen wir nun, dass der so genannte projektive Abschluss der nicht-ausgearteten Kegelschnitte Parabel,
Ellipse und Hyperbel jeweils eine kompakte Quadrik in P2 ist,
die die ∞-ferne Gerade in einem, keinem oder zwei Punkten
schneidet.
Ellipse, Parabel und Hyperbel sind in P2 projektiv äquivalent
(vgl. Aufgabe 1.3.8).
(1:0:0)
( x0 : x 1 : 0 )
(0:1:0)
Aufgabe 1.3.7:
Berechne die Schnittpunkte und ihre Vielfachheiten von a) der Ellipse
b) der Hyperbel x1 x2 = x20 mit der Geraden {x0 = 0}.
Aufgabe 1.3.8:
a11
Sei P = aa21
31
a12 a13
a22 a23
a32 a33
2
x21
a2
+
x22
b2
= x20 und
eine 3 × 3 - Matrix mit Determinante det P 6= 0. Diese definiert eine
Projektivität P : P → P2 , die auf den homogenen Koordinaten durch Multiplikation mit der
Matrix P wirkt: Da
a11 a12 a13 x0 a11 x0 +a12 x1 +a13 x2 a21 a22 a23
x1
= a21 x0 +a22 x1 +a23 x2 ,
a a a
x
31
32
33
2
a31 x0 +a32 x1 +a33 x2
gilt
P (x0 : x1 : x2 ) = (a11 x0 + a12 x1 + a13 x2 : a21 x0 + a22 x1 + a23 x2 : a31 x0 + a32 x1 + a33 x2 ).
Zwei Quadriken Q1 = 0 und Q2 = 0 in P2 heißen projektiv äquivalent, wenn es eine Projektivität P mit
Q1 P (x0 : x1 : x2 ) = Q2 (x0 : x1 : x2 )
gibt. Zeige, dass die Quadriken QParabel (x0 : x1 : x2 ) = x0 x2 − x21 = 0, QEllipse (x0 : x1 :
x2 ) =
x21
a2
+
x22
b2
− x20 = 0 und QHyperbel (x0 : x1 : x2 ) = x1 x2 − x20 = 0 projektiv äquivalent sind.
Aufgabe 1.3.9:
Untersuche, ob die Quadriken Q1 (x0 : x1 : x2 ) = x20 − x21 − x22 = 0 und Q2 (x0 : x1 : x2 ) =
x21 − x22 = 0 projektiv äquivalent sind.
2. Elliptische Kurven und der komplexe projektive Raum
In der Schule werden auch Funktionen höheren Grades untersucht. Betrachten wir als Beispiel die
Funktion dritten Grades f (x) = x3 − x. Nun ersetzen wir die Funktion wieder durch die affine Gleichung
und betrachten die affine Kurve
(x, y) ∈ R2 | mit y = x3 − x .
12
Verändern wir nun die Gleichung y = x3 − x, indem wir y durch sein Quadrat ersetzen, so treten wir
aus der Schulmathematik heraus. Die so erhaltene Kurve ist eine affine elliptische Kurve
(x, y) ∈ R2 | mit y 2 = x3 − x .
Wie wir im Folgenden sehen werden, verbirgt sich hinter den elliptischen Kurven eine Fülle von interessanter Geometrie. Anhand dieser elliptischen Kurven sollen nun verschiedenste Methoden der algebraischen Geometrie erklärt werden.
2.1 Der komplexe projektive Raum
Um ein vollständiges Bild eines geometrischen Objektes, wie zum Beispiel einer affinen Kurve, zu erhalten, haben wir im vorangegangenen Abschnitt die Kurve gemeinsam mit dem sie umgebenden Raum
R2 projektiv abgeschlossen. Wir haben also die ganze Situation im projektiven Raum P2 betrachtet.
Diese Maßnahme reicht aber in vielen Fällen nicht aus, um alle Eigenschaften einer Kurve zu entdecken.
Ein weiterer Schritt zur Vervollständigung des Bildes ist der algebraische Abschluss. Das heißt hier,
man ersetzt die reellen Zahlen R durch ihren so genannten algebraischen Abschluss, den Körper der
komplexen Zahlen C. Der Grund für diese Maßnahme liegt an der folgenden Tatsache:
Hauptsatz der Algebra
Ein Polynom vom Grad n über einem algebraisch abgeschlossenen Körper hat genau n Nullstellen.
Diese Nullstellen sind natürlich mit Vielfachheiten zu berechnen. (So hat zum Beispiel das Polynom
(x + 1)(x − 1)2 = 0 insgesamt drei Nullstellen, bei x = −1 eine Nullstelle der Vielfachheit 1 und bei
x = +1 eine Nullstelle der Vielfachheit 2.) Über den komplexen Zahlen schneidet deshalb jede Parabel
die x-Achse in 2 Punkten und jede Kubik hat genau 3 Nullstellen. Aus dem Satz folgt aber auch, dass
jede andere Gerade eine Parabel bzw. eine Kubik in genau 2 bzw. 3 Punkten schneidet.
Die komplexen Zahlen C lernt man manchmal in der Schule, spätestens aber im Studium kennen (für
eine Einführung in die komplexen Zahlen siehe auch [M1] und [M2]).
Als Vektorraum ist C isomorph zur reellen Ebene R2 . Die x-Achse von R2 entspricht dabei der reellen
Achse Re und die y-Achse der imaginären
Achse Im. Eine komplexe Zahl x + iy ∈ C stellt man sich
als Punkt (x, y) oder Vektor xy ∈ R2 vor. Man sagt zu C deshalb auch komplexe Zahlenebene. Der
projektive Abschluss der komplexen Zahlenebene, der eindimensionale komplexe projektive Raum P1 (C),
ist die Riemannsche Zahlenkugel :
Im
x+iy
8
iy
i
1 x
i
Re
1
Komplexe Zahlenebene

C
Riemannsche Zahlenkugel
π
/
C ∪ {∞} = P1 (C) = P1
Analog wie im Reellen gibt es hier genau einen ∞-fernen Punkt und eine Einbettung C ,→ P1 (C) der
komplexen Zahlen in den projektiven Raum.
Man kann den Zusammenhang zwischen Riemannscher Zahlenkugel und der komplexen Zahlenebene
auch mittels der stereographischen Projektion verstehen. Dabei ist die komplexe Zahlenebene genau das
Bild der stereographischen Projektion der Riemannschen Zahlenkugel mit dem Punkt ∞ als Projektionszentrum (zur stereographischen Projektion siehe [M3]).
13
Die Riemannsche Zahlenkugel P1 (C) ist auch ein Beispiel einer algebraischen Kurve. Darauf werden
wir später weiter eingehen.
Natürlich gibt es wie im Reellen auch komplexe projektive Räume höherer Dimension:
Pn (C)
Leider kann man sich aber schon P2 (C) nicht mehr bildlich vorstellen, da dieser Raum die reelle Dimension 4 hat. Rechnerisch ändert sich aber nicht viel. Für die komplexen projektiven Räume gelten
dieselben Regeln der homogenen Koordinaten
(Z0 : Z1 ) ∈ P1 (C)
und
(z0 : z1 : z2 ) ∈ P2 (C),
mit Z0 , Z1 , z0 , z1 , z2 ∈ C wobei wieder (Z0 , Z1 ) 6= (0, 0) und (z0 , z1 , z2 ) 6= (0, 0, 0). Um auf die Verwendung der komplexen Zahlen hinzuweisen, wurde hier und wird im Folgenden die Variable x bzw. xi
durch z bzw. zi ersetzt. Wie zuvor wird mittels Groß- und Kleinschreibung zwischen den homogenen
Koordinaten von P1 (C) und P2 (C) unterschieden. Da von nun an nur noch über den komplexen Zahlen
gearbeitet wird, schreiben wir
Pn (C) = Pn .
Aufgabe 2.1.10:
Eine Funktion f (z) := αz+β
γz+δ mit komplexen Zahlen α, β, γ und δ mit αδ − βγ 6= 0 heißt
Möbius-Transformation (siehe auch [M4]). Der Definitionsbereich von f ist Df = C\{− γδ }
und der Wertebereich ist Wf = C\{ αγ } (falls γ 6= 0), andernfalls Df = C und Wf = C. f kann
zu einer bijektiven Abbildung f : P1 → P1 fortgesetzt werden, indem man f (γ : −δ) := (0 :
1) und f (0 : 1) := (γ : α) setzt. Zeige, dass die Möbius-Transformation f eine Projektivität
ist.
Aufgabe 2.1.11:
Sind x, y, a, b komplexe Zahlen, so ist ihr Doppelverhältnis definiert durch
DV (x, y, a, b) :=
a) Zeige, dass DV (x, y, a, b) =
(x − a)(y − b)
(x − a) (y − a)
:
=
.
(x − b) (y − b)
(x − b)(y − a)
T V (x;a,b)
T V (y;a,b) .
b) Das Doppelverhältnis lässt sich zu einer Abbildung DV : P1 → P1 fortsetzen.
c) Zeige, dass das Doppelverhältnis unter Möbius-Transformationen invariant ist.
Aufgabe 2.1.12:
Beweise: Zu je drei verschiedenen komplexen Zahlen z1 , z2 , z3 und v1 , v2 , v3 gibt es genau eine
Möbius-Transformation f mit f (zi ) = vi für i = 1, 2, 3.
Aufgabe 2.1.13:
Beweise: Zwei Quadrupel x, y, a, b und x0 , y 0 , a0 , b0 komplexer Zahlen sind genau dann projektiv
äquivalent, wenn ihre Doppelverhältnisse gleich sind.
Aufgabe 2.1.14:
Finde die Möbius-Transformation f , die die Punkte 1, i, −1 auf 0, 1, ∞ in der gegebenen
Reihenfolge abbildet.
Aufgabe 2.1.15:
Seien x, y, a, b paarweise verschiedene komplexe Zahlen. Man sagt, das Punktepaar x, y trennt
die Punkte a, b harmonisch, wenn DV (x, y, a, b) = −1. Zeige, das x, y das Paar a, b genau
dann harmonisch trennt, wenn es eine Möbius-Transformation gibt, die a, b fixiert und x, y
vertauscht.
14
2.2 Elliptische Kurven in P2
Eine elliptische Kurve ist nach Definition eine singularitätenfreie (zwVnn) ebene Kurve vom Grad 3.
Die allgemeine Gleichung einer affinen elliptischen Kurve ist (vgl. [Si] p.46)
y 2 = az 3 + bz 2 + cz + d.
Durch eine Koordinatentransformationen kann diese Gleichung auf die Weierstraßsche Normalform
y 2 = 4z 3 − g2 z − g3
(9)
gebracht werden (vgl. Aufgabe 2.2.16).
Bemerkung 2. Die Bezeichnung der Koeffizienten g2 und g3 beruht auf dem Zugang zu elliptischen
Kurven via der Weierstraßschen ℘ -Funktion. Hierbei sind die Koeffizienten die Eisensteinreihen
g2 = 60G4 und g3 = 140G6 und hängen ausschließlich vom Periodengitter der ℘ -Funktion ab. Hierauf
soll im Folgenden nicht weiter eingegangen werden. Näheres dazu findet man in [FB].
Durch Homogenisieren von (9) erhalten wir den projektiven Abschluss der affinen elliptischen Kurve,
also die Kubik:
E:
z0 z22 = 4z13 − g2 z02 z1 − g3 z03
Nach dem Hauptsatz der Algebra schneidet eine Kubik jede Gerade genau dreimal. Insbesondere schneidet die elliptische Kurve E die ∞-ferne Gerade dreimal. Rechnerisch erhalten wir Folgendes:
E ∩ ∞-ferne Gerade = z0 z22 = 4z13 − g2 z02 z1 − g3 z03 ∩ z0 = 0
= (0 : z1 : z2 ) 0 = 4z13 = {(0 : 0 : 1)}
Das bedeutet, die elliptische Kurve E schneidet die ∞-ferne Gerade in dem Punkt (0 : 0 : 1). Da sich
aber dieser Punkt als Lösung der Gleichung 0 = 4z13 ergibt, hat dieser Schnittpunkt die Vielfachheit
drei.
In der algebraischen Geometrie sagt und schreibt man (zwVnn), dass
D := E · z0 = 0 = 3 (0 : 0 : 1)
ein Divisor vom Grad drei auf E ist. Die Schreibweise E · z0 = 0 bedeutet etwa ”Durchschnitt mit
Vielfachheit”. Divisoren und Linearsysteme werden in Abschnitt 3.2 diskutiert.
Aufgabe 2.2.16:
Finde die Koordinatentransformation, die die allgemeine Gleichung y 2 = az 3 + bz 2 + cz + d
einer elliptischen Kurve auf die Weierstrasssche Normalform bringt.
Aufgabe 2.2.17:
Zeige, dass der projektive Abschluss der affinen Kubik K : y = x3 − x geometrisch zur
Neilschen Parabel mit der affinen Gleichung y 2 = x3 äquivalent ist (siehe auch Aufgabe
2.5.20) .
2.3 Die Überlagerung E −→ P1
Wie zuvor erwähnt ist neben E auch P1 eine algebraische Kurve. Anhand dieser Kurven kann man das
Phänomen der Überlagerung erklären. Genauer, die elliptische Kurve E ist eine doppelte Überlagerung
von P1 . Das sieht man am einfachsten so: Die elliptische Kurve E ist mengentheoretisch die Menge
der Lösungen (z, y) der affinen Gleichung (9) zusammen mit dem ∞-fernen Punkt (0 : 0 : 1). Nun
definiert man die Abbildung Vergiss y: (z, y) 7→ (1 : z) und bildet gleichzeitig den ∞-fernen Punkt
(0 : 0 : 1) ∈ P2 auf den ∞-fernen Punkt (0 : 1) ∈ P1 ab. Da in der Gleichung (9) die Variable y nur als
15
Quadrat vorkommt, gibt es zu jedem Punkt (z, y) ∈ E auch noch den Punkt (z, −y) ∈ E und unter der
Abbildung Vergiß y werden diese beiden Punkte auf denselben Punkt (1 : z) ∈ P1 abgebildet:
 
y 2 = 4z 3 − g2 z − g3 ∪ {∞} = E




(z, ±y)
(0 : 0 : 1)
Vergiss y :
2:1
_
_





z = (1 : z)
(0 : 1)
P1
Die Abbildung E −→ P1 ist damit vom Grad 2, dass heißt, (fast) jeder Bildpunkt hat zwei Urbilder in
E. Die 3 Nullstellen p1 , p2 und p3 von 4z 3 − g2 z − g3 definieren Punkte P1 = (1 : p1 ), P2 = (1 : p2 ) und
P3 = (1 : p3 ) ∈ P1 , die wie auch der Punkt ∞ = (0 : 1) jeweils nur ein Urbild haben. Man sagt: E ist
eine doppelte Überlagerung von P1 , verzweigt in den vier Punkten P1 P2 , P3 und (0 : 1). In Abschnitt
3.4 werden wir diese Überlagerung topologisch betrachten und so ein anschauliches Bild erhalten.
2.4 Das Additionstheorem
Unter den algebraischen Kurven nehmen die elliptischen Kurven eine Sonderstellung ein, denn sie haben
die Struktur einer abelschen Gruppe. Aus geometrischer Sicht beruht dieses auf dem
C
B
Additionstheorem:
Drei Punkte A, B und C auf einer elliptischen Kurve haben genau dann die Summe Null, wenn sie auf einer Geraden liegen:
A + B + C = 0.
A
A+B=-C
Das Additionstheorem lässt sich auch rein analytisch mit Hilfe der Weierstraßschen ℘ -Funktion
beweisen (siehe dazu [FB]). In der vorliegenden Arbeit soll diese Gruppeneigenschaft geometrisch begründet werden. Dazu müssen wir uns eingehender mit den vielfältigen Eigenschaften elliptischer Kurven
beschäftigen. Zunächst betrachten wir dazu Thetafunktionen.
2.5 Thetafunktionen
Die klassische Riemannsche Thetafunktion ist die Funktion:
X
ϑ(v) = ϑ(v, z) =
ekπi(kz+2v)
(10)
k∈Z
mit komplexen Zahlen v und z, wobei z einen positiven Imaginärteil hat: Im z > 0. ϑ ist komplex
differenzierbar in v und z (zwVnn). Bei der Summendarstellung der Funktion handelt es sich um eine
Fourierreihe (zwVnn). Ausschlaggebend für die Eigenschaften der Thetafunktion ist die Periodizität der
Exponentialfunktion e : C → C:
e2πi·k = 1, für alle k ∈ Z.
(11)
Damit lassen sich die folgenden Funktionaleigenschaften der Thetafunktion nachweisen (für Beweise
siehe Aufgabe 2.5.18 oder [BL2] Abschnitte 3.2 und 8.5):
1. ϑ ist periodisch bezüglich Z ⊂ C:
ϑ(v + n) = ϑ(v)
für alle v ∈ C und n ∈ Z
und
(12)
2. ϑ ist semiperiodisch bezüglich der ganzzahligen Vielfachen der komplexen Zahl z:
ϑ(v + nz) = e−πi(n
2
z+2nv)
ϑ(v)
für alle v ∈ C und n ∈ Z.
(13)
16
Aus der Riemannschen Thetafunktion leiten sich die so genannten Thetafunktionen mit hCharakteristik
i
h2i
m
1
ab. Wir benötigen nur die drei Thetafunktionen mit den Charakteristiken 00 , 03 und 03 .
n
Dazu ersetzt man in Definition (10) k durch (k + 3c ) mit c = 0, 1 oder 2 und erhält:
X (k+ c )πi (k+ c )z+2v
c
3
für c = 0, 1, 2.
e 3
ϑ 03 (v) :=
k∈Z
Nach Definition ist die Thetafunktion ϑ 00 identisch zur Riemannschen Thetafunktion ϑ. Diese drei
neuen Thetafunktionen haben ebenfalls die Funktionalgleichungen (12) und (13) (vgl. Aufgabe 2.5.19):
c
c
2
ϑ 03 (v + n1 z + n2 3) = e−πi(n1 z+2n1 v) ϑ 03 (v)
für alle n1 , n2 ∈ Z und v ∈ C.
(14)
Bei der Definition der Riemannschen Thetafunktion wurde vorausgesetzt, dass die komplexe Zahl z
einen positiven Imaginärteil hat. Das heißt, z liegt
in der so genannten oberen Halbebene der komplexen Zahlenebene. Deshalb spannen die ganzzahligen
Vielfachen von z und 3, also alle komplexen Zahlen
der Form n1 z + n2 3 mit n1 , n2 ∈ Z, ein Gitter
Im
Zz + Z 3 ⊂ C
z
in der komplexen Zahlenebene auf (siehe nebenstehende Graphik).
0
3
Re
Wir betrachten nun die Abbildung:
φ : C 3 v 7→
h2i h1i
ϑ 00 (v) : ϑ 03 (v) : ϑ 03 (v) ∈ P2
(15)
Da die drei Thetafunktionen derselben Funktionaleigenschaft (14) genügen und da bei homogenen Koordinaten gleiche Faktoren gekürzt werden können, ist diese Abbildung periodisch bezüglich des Gitters
Zz + Z3. Das heißt:
φ(v + w) = φ(v)
für alle
v∈C
und alle
w ∈ Zz + Z 3.
Die Abbildung φ induziert eine projektive Einbettung des Quotientenraumes C/(Zz + Z3):
C YYYYYYYYφ
YYYYYY
YY,
π
fff2 P2
ϕ
f
f
f
f
f
% fff
C/(Zz + Z3)
Der Quotient C/(Zz + Z 3) wird im nächsten Abschnitt genauer besprochen. Mehr zu der Einbettung
ϕ findet man in Abschnitt 3.3.
Aufgabe 2.5.18:
Beweise die Funktionaleigenschaften (12) und (13) der Riemannschen Thetafunktion ϑ. Hinweis: Benutze die Reihendarstellung von ϑ.
Aufgabe 2.5.19:
Beweise die Funktionaleigenschaft (14) der Thetafunktionen ϑ
c
3 .
0
Aufgabe 2.5.20:
Bestimme die affine und homogene Gleichung der Bildkurve der Abbildung ϕ1 : P1 → P2 mit
(Z0 : Z1 ) 7→ (Z03 : Z0 Z12 : Z13 ). Um welche Kurve handelt es sich und was sind die ∞-fernen
Punkte? Zeichne die affine Kurve, was fällt auf?
Aufgabe 2.5.21:
Bestimme die affine und homogene Gleichung der Bildkurve der Abbildung ϕ2 : P1 → P2 mit
(Z0 : Z1 ) 7→ (Z03 : Z0 Z12 − Z03 : Z13 − Z02 Z1 ). Um welche Kurve handelt es sich und was sind
die ∞-fernen Punkte? Zeichne die affine Kurve, was fällt auf?
17
2.6 Thetarelationen
Das Bild projektiver Einbettungen (wie oben definiert) wird durch Thetarelationen beschrieben. Die
klassischen Riemannschen Thetarelationen (zwVnn) lauten:
2g · ϑ[a](v1 , Z) · ϑ[a + b1 ](v2 ) · ϑ[a + b2 ](v3 , Z) · ϑ[a − b1 − b2 ](v4 , Z) =
X
t
t
e4πi(a1 c2 −a2 c1 ) · ϑ[c](v1 + v2 + v3 + v4 , Z) · ϑ[c + b1 ](v1 + v2 − v3 − v4 , Z)
c∈ 12 Z2g /Z2g
· ϑ[c + b2 ](v1 − v2 + v3 − v4 , Z) · ϑ[c − b1 − b2 ](v1 − v2 − v3 + v4 , Z)
mit Z ∈ Hg , der Siegelschen oberen Halbebene der Dimension g, v1 , . . . , v4 ∈ Cg , und a, b1 , b2 ∈ 21 Z2g
(siehe [K]). Hier benötigen wir die kubischen Thetarelationen (zwVnn) (vgl. [BL1]):
X
L
L
ρ(z) · ϑL
Θ(y1 ,y2 ),ρ (0) ·
y10 +y20 +y3 +2z · ϑy10 −y20 +y3 +2z · ϑ−2y10 +y3 +2z
z∈Z6
= Θ(y10 ,y20 ),ρ (0) ·
X
L
L
ρ(z) · ϑL
y1 +y2 +y3 +2z · ϑy1 −y2 +y3 +2z · ϑ−2y1 +y3 +2z
z∈Z6
Hiervon benötigen wir nur den Spezialfall der Dimension g = 1 und mit dem Geradenbündel L = O(3)
zuvor. In diesem Fall reduzieren sich die kubischen Thetarelationen zu der folgenden Gleichung (vgl.
[BL2] Exercise 7.(8)) (zwVnn):
h 2 i3
h1i h2i
h 1 i3
3
Θ
(0) 0 3
ϑ 00 + ϑ 03 + ϑ 03 = 3 Θ(0,0),1
ϑ
ϑ
ϑ 03
(16)
0
0
(0,6),1 (0)
Θ
(0)
ist eine komplexe Konstante 6= 0, die sich mit gewissen Thetafunktionen berechnen
Der Term 3 Θ(0,0),1
(0,6),1 (0)
lässt, für uns hier aber nicht von Bedeutung
ist. (16)histieine Relation zwischen den Komponenten der
0 h 1 i
2
3
Abbildung (15). Ersetzt man hier ϑ 0 , ϑ 0 und ϑ 03 durch die homogenen Koordinatenfunktionen
z0 , z1 und z2 von P2 , so erhalten wir die Gleichung
Θ
(0)
z0 z1 z2 .
z03 + z13 + z23 = 3 Θ(0,0),1
(0,6),1 (0)
(17)
Dies ist die Gleichung der Bildkurve von φ bzw. ϕ. Da dieses eine Gleichung vom Grad 3 ist, ist φ(C) eine
elliptische Kurve, die wieder mit E bezeichnet werden soll. Da ϕ : C/(Zz + Z3) ,→ P2 eine Einbettung
ist, ergeben sich die folgenden Identifikationen:
Θ(0,0),1 (0)
2
E ' C/(Zz + Z3) ' (z0 : z1 : z2 ) z03 + z13 + z23 = 3 Θ(0,6),1
(0) z0 z1 z2 ⊂ P
Aufgabe 2.6.22:
Θ
(0)
(0,0),1
Berechne die Schnittpunkte der elliptischen Kurve E : z03 + z13 + z23 = 3 Θ(0,6),1
(0) z0 z1 z2 mit
der ∞-fernen Gerade z0 = 0.
2.7 Die elliptische Kurve E als komplexer Torus
Betrachten wir zunächst den Quotienten C/(Zz+Z3). Wie in Abschnitt 2.5 gezeigt wurde, ist Zz+Z3 ein
Gitter in C. Der Quotient C/(Zz +Z3) ist nach Definition die Menge aller Nebenklassen v := v +Zz +Z3
mit v ∈ C (vgl. Aufgabe 2.7.23). Anschaulich kann man sich den Quotienten folgendermaßen vorstellen:
Man betrachtet im Gitter Zz + Z3 das von den vier Eckpunkten 0, 3, z und z + 3 gebildete Fundamentalparallelogramm und identifiziert gegenüberliegende Seiten. So entsteht ein komplexer Torus:
c
z
d
0
b
a
3
¼
a=c
b=d
18
Hierbei ist π die Projektion:
π : C −→ C/(Zz + Z3) = E
mit
v 7→ v := v + Zz + Z3
Die komplexen Zahlen C sind als Körper insbesondere auch eine abelsche Gruppe. Diese Gruppenstruktur induziert eine Gruppenstruktur auf dem komplexen Torus E = C/(Zz + Z3) und wir erhalten
die geometrische Erklärung des Additionstheorems.
Fassen wir zusammen: Die elliptische Kurve E wird durch die algebraische Gleichung
Θ
(0)
(0,0),1
z03 + z13 + z23 = 3 Θ(0,6),1
(0) z0 z1 z2
beschrieben, ist also eine projektive algebraische Kurve. Damit ist aber auch der komplexe Torus E =
C/(Zz + Z3) algebraisch. Als algebraischer komplexer Torus der Dimension 1 ist E schließlich eine
projektive algebraische Kurve vom Geschlecht 1 (siehe auch Abschnitt 3.1).
Aufgabe 2.7.23:
Seien u und v ∈ C und n ∈ Zz + Z3. Zeige, dass in E = C/(Zz + Z3) gilt:
a) u = v genau dann, wenn u − v ∈ Zz + Z3.
b) n = 0.
c) u + v = u + v.
3. Einige Sätze über algebraische Kurven
In diesem letzten Teil sollen einige klassische Aussagen und Sätze der algebraischen Geometrie, insbesondere der Kurventheorie, vorgestellt werden. Unter Kurve verstehen wir hier immer eine glatte, das heißt
singularitätenfreie Kurve (zwVnn). Beispiele für Kurven mit Singularitäten findet man in Aufgaben
2.5.20 und 2.5.21.
3.1 Das Geschlecht einer algebraischen Kurve
Eine projektive algebraische Kurve C vom Geschlecht g kann man sich topologisch als eine kompakte
Fläche mit g Löchern vorstellen:
¸1
¸g+1
¸g
¸2
¸2g
¸g+2
Neben dieser anschaulichen Erklärung kann das Geschlecht g einer Kurve C z. B. auch über die Dimensionen bzw. Ordnungen der folgenden Kohomologie bzw. Homologiegruppen definiert werden:
H 0 (C, O(K)) ' Cg ,
H1 (C, Z) ' Z2g .
Die Kohomologie H 0 (C, O(K)) wird im nächsten Abschnitt erklärt. Die Elemente der Homologiegruppe
H1 (C, Z) sind Äquivalenzklassen von geschlossenen Zykeln, also reell eindimensionalen geschlossenen
Kurven auf C. Zwei solche Zykel sind äquivalent, wenn sie stetig ineinander deformierbar sind. So sind
beispielsweise die in der obigen Graphik eingezeichneten Zykel λ1 und λ2 nicht äquivalent, da sie sich
um verschiedene Löcher winden. Die Zykel λ1 , . . . , λ2g sind Repräsentanten eines Erzeugendensystems
für H1 (C, Z) ' Z2g . An dieser Definition bzw. der Graphik erkennt man sofort, dass die Kurven P1 das
Geschlecht 0 (da kein Loch) und E das Geschlecht 1 (da ein Loch) haben.
19
3.2 Divisoren
Ein Divisor D auf einer Kurve C ist eine formale endliche Summe von Punkten auf C:
D = n 1 P1 + · · · + n k Pk ,
mit ni ∈ Z und Pi ∈ C.
Der Grad des Divisors ist
deg D := n1 + · · · + nk .
Beispiel 1. Am Ende von Abschnitt 2.2 haben wir schon einmal einen Divisor kennengelernt, den
Divisor
D := E · z0 = 0 = 3 (0 : 0 : 1)
auf der elliptischen Kurve E = z0 z22 = 4z13 − g2 z02 z1 − g3 z03 .
Jede rationale Funktion f auf C definiert einen Divisor. Dazu berechnet man die Nullstellen N von f
und ihre Ordnungen νN (wie man es aus der Schule kennt). Ebenfalls berechnet man alle Pole P von f
und ihre Ordnungen νP . Die Pole sind hierbei gerade die Nullstellen des Nenners. (So hat beispielsweise
die Funktion z 7→ 1−z
z 2 bei z = 1 eine Nullstelle der Ordnung 1 und bei z = 0 einen Pol der Ordnung 2.)
Der Divisor der Funktion f ist nun
X
X
(f ) =
νN N −
νP P.
N Nullstelle von f
P Pol von f
Die Divisoren (f ) heißen Hauptdivisoren. Rationale Funktionen auf einer algebraischen Kurve bedürfen
eigentlich einer genaueren Definition, wir wollen es hier bei einer Erklärung mittels eines Beispiels
belassen:
Beispiel 2. Rationale Funktionen auf C = P1 sind Quotienten
p(Z0 ,Z1 )
q(Z0 ,Z1 )
mit homogenen Polynomen
1
p und q in Z0 und Z1 und deg p = deg q. Betrachten wir beispielsweise f (Z0 , Z1 ) := Z
Z0 . f hat in
(1 :0) eine einfache Nullstelle und in ∞ = (0 : 1) einen einfachen Pol. Der Hauptdivisor von f ist also
f1 = (1 : 0) − (0 : 1) und deg f = 1 − 1 = 0.
Wie in diesem Beispiel gilt allgemein für den Grad von Hauptdivisoren:
deg f = 0.
Beispiel 3. Ein weiteres Beispiel für einen Divisor ist der Verzweigungsdivisor der doppelten Überlagerung Vergiss y : E 7→ P1 aus Abschnitt 2.3. Die vier Verzweigungspunkte bilden den so genannten
Verzweigungsdivisor R = P1 + P2 + P3 + (0 : 1) auf P1 .
Sind
D1 =
X
nP P
und D2 =
P ∈C
X
mP P
P
Divisoren auf einer Kurve C (nach Definition sind in dieser Darstellung nur endlich viele Koeffizienten
nP 6= 0 bzw. mp 6= 0), so definiert man die Addition
X
D1 + D2 =
(nP + mP )P
P
und die Ordnungsrelation
D1 ≥ D2 ,
für alle P ∈ C.
Die rationalen Funktionen f auf C, deren Hauptdivisor f in diesem Sinne ≥ −D ist, bilden bezüglich
der Addition von Funktionen und der Skalarmultiplikation, also der einfachen Multiplikation mit einer
komplexen Zahl, einen komplexen Vektorraum. Dieser Vektorraum stimmt mit der 0-ten Kohomologie
H 0 (C, O(D)) des Divisors D überein. Es gilt also:
H 0 (C, O(D)) := f f ist eine rationale Funktion auf C mit f ≥ −D .
falls
nP ≥ mP
20
Bei den Elementen von H 0 (C, O(D)) handelt es sich also um rationale Funktionen, deren Null- und
Polstellen mit ihren Vielfachheiten durch den Divisor D abgeschätzt werden. Dazu ein Beispiel:
Beispiel 4. Sei D := 2∞ = 2(0 : 1) auf C = P1 . Eine rationale Funktion f mit f ≥ −D = −2(0 : 1)
darf also nur in ∞ = (0 : 1) einen Pol haben und zwar höchstens vom Grad 2. Damit ist f von der Form
f = Zp2 mit einem homogenen Polynom p vom Grad 2. Der Vektorraum der homogenen Polynome vom
0
Grad 2 in den Variablen Z0 und Z1 wird aber von Z02 , Z0 Z1 und Z12 aufgespannt. Somit ist
Z02
Z02
= 1,
Z0 Z1
Z02
=
Z1
Z0 ,
und
Z12
Z02
eine Basis von H 0 (P1 , O(2∞)).
0
Beispiel 5. Für jede
der rationalen
projektive algebraische Kurve C ist H (C, O) der Vektorraum
Funktionen f mit f ≥ 0. Deshalb kann f keine Pole haben. Da aber wegen deg f = 0 die Funktion
f genauso viele Nullstellen wie Pole (mit Vielfachheiten gerechnet) hat, besitzt f auch keine Nullstellen
und ist somit konstant. Der Vektorraum H 0 (C, O) wird somit von der konstanten Funktion 1 erzeugt
und ist eindimensional.
Beispiel 6. Ist der Grad einesDivisors D negativ, so gibt es keine rationale Funktion f mit f ≥
−D, denn sonst wäre 0 = deg f ≥ deg(−D) = − deg D > 0, ein Widerspruch! Somit gilt für Divisoren
negativen Grades, dass h0 (C, O(D)) = dim H 0 (C, O(D)) = 0.
Wie wir in diesen Beispielen sehen, ist die Kohomologie H 0 (C, O(D)) ein Vektorraum endlicher Dimension. Die Dimension von H 0 (C, O(D)) wird mit h0 (C, O(D)) bezeichnet.
Auf einer projektiven algebraischen Kurve C vom Geschlecht g gibt es einen speziellen Divisor, den
kanonischen Divisor K. Der kanonische Divisor wird mittels rationaler Differentialformen auf C definiert
(zwVnn). Insbesondere ist K ein Indikator für das Geschlecht von C, denn wie in Abschnitt 3.1 schon
erwähnt gilt h0 (C, O(K)) = g.
Sei D ein Divisor auf einer Kurve C mit h0 (C, O(D)) = n ≥ 2 und f0 , . . . , fn−1 eine Basis von
H 0 (C, O(D)). D heißt basispunktfrei, wenn die Funktionen f0 , . . . , fn−1 keine gemeinsame Nullstelle
haben. In diesem Fall definiert D die Abbildung
ϕD : C → Pn−1 , ϕ(P ) = f0 (P ) : · · · : fn−1 (P ) .
Ist diese Abbildung zusätzlich auch noch eine Einbettung, so sagt man, der Divisor D ist sehr ampel.
Z2
Z2
Z1
und Z12 haben offensichtlich
Beispiel 7. (Fortsetzung von Beispiel 4) Die Funktionen Z02 = 1, ZZ0 Z2 1 = Z
0
0
0
0
keine gemeinsame Nullstelle. Der Divisor D := 2∞ = 2(0 : 1) ist also basispunktfrei und definiert die
Abbildung
Z12
2
2
1
ϕD : P1 → P2 , (Z0 : Z1 ) 7→ (1 : Z
Z0 : Z 2 ) = (Z0 : Z0 Z1 : Z1 ).
0
z12
Das Bild von ϕD genügt der Gleichung z0 z2 − = 0. Das ist aber genau die homogene Gleichung (8)
der projektiv abgeschlossenen Parabel (vgl. Abschnitt 1.3). Der Divisor D = 2∞ ist genau der Divisor
der ∞-fernen Punkte der Parabel. Da D sogar sehr ampel ist und damit ϕD eine Einbettung, ist die
abgeschlossene Parabel eine Darstellung der projektiven Gerade P1 in P2 .
An diesem Beispiel sieht man noch eine weitere Eigenschaft eines sehr amplen Divisors D und seiner
zugehörigen Einbettung ϕD : Der Grad des Divisors ist gleich dem Grad der Bildkurve:
deg D = deg ϕD (C).
21
3.3 Der Satz von Riemann-Roch
Hierbei handelt es sich um den folgenden klassischen Satz der algebraischen Geometrie (vgl. [Ha] p.295
oder [ACGH] p.7):
Der Satz von Riemann-Roch:
Für einen Divisor D auf einer projektiven Kurve C vom Geschlecht g gilt:
h0 (C, O(D)) − h0 (C, O(K − D)) = deg D + 1 − g
Die folgenden Beispiele zeigen, wie der Satz von Riemann-Roch verwendet wird:
Beispiel 8. Nach Abschnitt 3.1 gilt für den kanonischen Divisor K einer algebraischen Kurve C vom
Geschlecht g, dass h0 (C, O(K)) = g. Nach dem Satz von Riemann-Roch folgt für den Grad von K
deg K = h0 (C, O(K)) − h0 (C, O(C)) − 1 + g = g − 1 − 1 + g = 2g − 2.
Ist g ≥ 2 und C nicht hyperelliptisch (siehe Abschnitt 3.4), so ist K sehr ampel und definiert die so
genannte kanonische Einbettung ϕωC : C ,→ Pg−1 (zwVnn).
Θ
(0)
(0,0),1
Beispiel 9. Die elliptische Kurve E : z03 + z13 + z23 = 3 Θ(0,6),1
(0) z0 z1 z2 aus den Abschnitten 2.5 bis
2.7 schneidet die ∞-ferne Gerade z0 = 0 in drei Punkten P1 , P2 und P3 (vgl. Aufgabe 2.6.22). Diese
bilden einen Divisor D := P1 + P2 + P3 vom Grad 3. Da E das Geschlecht g = 1 hat, ist der Grad
deg(K − D) = deg K − deg D = 2g − 2 − 3 = 2 − 2 − 3 = −3 < 0. Somit gilt nach Abschnitt 3.2,
Beispiel 6, dass h0 (E, O(K − D)) = 0. Nach Riemann-Roch gilt:
h0 (E, O(D)) = h0 (E, O(K − D)) + deg D + 1 − g
=0+3+1−1=3
h1i
h 2 i
Eine Basis von H 0 (E, O(D)) ist durch die drei Thetafunktionen ϑ 00 , ϑ 03 , ϑ 03
gegeben und
ϕD ist die Einbettung ϕ : E ,→ P2 aus Abschnitt 2.5. Insbesondere ist D sehr ampel (zwVnn).
3.4 Überlagerungen algebraischer Kurven
In Abschnitt 2.3 haben wir mit der Abbildung Vergiss y : E → P1 ein erstes Beispiel einer Überlagerung algebraischer Kurven kennen gelernt. Die Hurwitz-Formel (vgl. [Ha], p. 301) beschreibt, wie die
Geschlechter der Kurven einer Überlagerung zusammenhängen.
Hurwitz-Formel:
n:1
Für eine Überlagerung f : C −→ C 0 von projektiven Kurven vom Geschlecht g und g 0 und Verzwei0
gungsdivisor R (auf C ) gilt:
2g − 2 = n(2g 0 − 2) + deg R
Beispiel 10. Wir wenden diesen Satz auf die in Abschnitt 2.3 behandelte Überlagerung der elliptischen
Kurve von P1 an. Wir hatten gesehen, dass die Überlagerung E→P1 vom Grad 2 war, deshalb muss
nach der Hurwitz-Formel der Verzweigungsdivisor den Grad
deg R = 2gE − 2 − 2(2gP1 − 2) = 2 · 1 − 2 − 2(2 · 0 − 2) = 4
haben.
22
Dieses bestätigt unsere Beobachtung, dass die Überlagerung
in 4 Punkten verzweigt ist. Diese 4 Verzweigungspunkte werden auch durch das topologische Bild in der nebenstehenden
Graphik deutlich: Hier sind auf der Riemannschen Zahlenkugel P1 die vier Verzweigungspunkte markiert. Entlang von je
zwei Punkten wird P1 aufgeschlitzt, das ist rechts unten in
der Graphik dargestellt. Von dieser aufgeschlitzten Zahlenkugel betrachtet man zwei Kopien (links unten in der Graphik).
Diese beiden Flächen werden entlang der Schlitze miteinander
verklebt. Das liefert den Torus E. Die Abbildung E → P1 ist
nun durch Identifikation sich entsprechender Punkte auf den
beiden Kopien definiert.
E
IP
1
Kurven beliebigen Geschlechtes, die wie elliptische Kurven doppelte Überlagerungen von P1 sind, werden hyperelliptische Kurven genannt. Ebene hyperelliptische Kurven werden durch Gleichungen der
folgenden Form beschrieben:
C = { (z, y) | y 2 = f (z) } ⊂ P2
Hier ist f ∈ C[z] ein Polynom und der Querstrich über der Mengenklammer bedeutet den projektiven
Abschluss. Das Geschlecht von C ist abhängig vom Grad des Polynoms f :
g=
deg f −1
,
2
wenn deg f ungerade,
und
g=
deg f
2
− 1,
wenn deg f gerade.
Genau wie bei den elliptischen Kurven in Abschnitt 2.3 definiert die Zuordnung Vergiss y: (z, y) 7→ z
2:1
eine doppelte Überlagerung C −→ P1 . Nach der Hurwitz-Formel gilt für den Verzweigungsdivisor
deg R = 2g − 2 − 2(2gP1 − 2) = 2g + 2 = 2(g + 1).
Analog wie bei der doppelten Überlagerung E → P1
ist auch die topologische Darstellung dieser Überlagerung zu verstehen: Der Verzweigungsdivisor R
besteht aus g + 1 Paaren von Punkten. Unten in der
Graphik ist der entlang dieser Punktepaare aufgeschlitzte P1 abgebildet. Darüber sieht man die zwei,
entlang dieser Schlitze verklebten Kopien, die auf
diese Weise eine kompakte Riemannsche Fläche mit
g Löchern bilden.
3.5 Jacobische Varietäten
Sei C eine algebraische Kurve vom Geschlecht g. Die Kohomologiegruppe H 0 (C, O(K)) des kanonischen
Geradenbündels ist der Vektorraum der holomorphen Differentiale auf der Kurve C. Ist C hyperelliptisch:
C = { (z, y) | y 2 = f (z) } ⊂ P2 ,
so kann man einfach eine Basis von H 0 (ωC ) angeben:
ω1 :=
dz
√
,
f
dz
dz
ω1 := z √
, . . . , ωg := z g−1 √
f
f
So wie man in der Funktionentheorie lernt, holomophe Funktionen in Bereichen der komplexen Zahlenebene zu integrieren, so kann man das auch mit Differentialen auf C. Nach dem Cauchyschen Integralsatz sind Integrale holomorpher Funktionen bzw.
Differentiale wegunabhängig, allerdings nur auf einp
fach zusammenhängenden Gebieten. Aufgrund der
p
0
Löcher trifft das für C nicht zu. Deshalb ist das Integral
Z p
ωi
p0
23
nur modulo der Integrale
R
λ
ωi , mit λ ∈ H1 (C, Z) bestimmt. Damit definiert die Zuordnung
Rp ω 
Rpp0

C 3 p 7→ 

p0
..
R p.
p0
1
ω2

 ∈ Cg

ωg
eine Abbildung C ,→ Cg /H1 (C, Z). Der Quotient Cg /H1 (C, Z) ist ein algebraischer kompakter komplexer Torus der Dimension g, die Jacobische Varietät der Kurve C:
Jac(C) := Cg /H1 (C, Z)
(vgl. [BL2] Chapter 11). Die Jacobische Varietät Jac(C) ist ein Beispiel für eine abelsche Varietät.
3.6 Abelsche Varietäten
Abelsche Varietäten sind nach Definition algebraische komplexe Tori. Ein komplexer Torus ist ein
Quotient:
X = C g /Λ, mit einem Gitter Λ ⊂ Cg , Λ ' Z2g .
Der komplexe Torus X heißt algebraisch, wenn es eine projektive Einbettung X ,→ Pn gibt. Das ist
bei den Jacobischen Varietäten immer der Fall. Ein erstes Beispiel für eine abelsche Varietät haben
wir in Abschnitt 2.7 mit den elliptischen Kurven schon kennen gelernt: Eine elliptische Kurve ist ein
komplexer Torus der Dimension 1:
E = C/(Zz + Z3)
Da es die projektive Einbettung ϕ : E ,→ P2 gibt, ist E eine projektive algebraische Kurve. Andererseits
sagt die Einbettung ϕ : E ,→ P2 , dass der komplexe Torus E = C/(Zz + Z3) ein algebraischer Torus,
also ein abelsche Varietät ist. Die algebraische Kurve E ist identisch mit ihrer Jacobischen Varietät:
Jac(E) = E
3.7 Prymvarietäten
Ein weiteres Beispiel von abelschen Varietäten, die C
in engem Zusammenhang zu Kurven stehen, sind
die Prymvarietäten. Dazu betrachte man eine unverzweigte doppelte Überlagerung projektiver Kurven
2:1
π : C −→ C 0 .
¼
C'
Nach der Hurwitz-Formel hängen die Geschlechter der beiden Kurven folgendermaßen zusammen:
g(C 0 ) = g + 1
⇒
g(C) = 2g + 1.
2:1
Die Überlagerung π : C −→ C 0 induziert einen Homomorphismus von Homologiegruppen
π∗ : H1 (C, Z) −→ H1 (C 0 , Z)
und dieser wiederum einen Homomorphismus abelscher Varietäten, die so genannte Normabbildung
Nπ : Jac(C) −→ Jac(C 0 ).
Der Kern der Normabbildung, also das, was auf null abgebildet wird, besteht in diesem Fall aus zwei
Zusammenhangskomponenten. Da Nπ aber auch ein Gruppenhomomorphismus ist, ist der Kern wieder eine abelsche Gruppe, und insbesondere ist die Komponente, die die Null enthält, eine abelsche
2:1
Varietät, die Prymvarietät der Überlagerung π : C −→ C 0 :
P rym(C, C 0 ) = ker Nπ 0 = Cg /H1 (C, Z)−
24
(vgl. [BL2] Chapter 12). Jacobische Varietäten und Prymvarietäten erben bzw. spiegeln wider eine
Fülle geometrischer Eigenschaften der zugrunde liegenden Kurven. So spielen diese abelschen Varietäten
eine wichtige Rolle in der Theorie der algebraischen Kurven und umgekehrt werden die algebraischen
Kurven bei der Untersuchung abelscher Varietäten benutzt.
Abelsche Varietäten spielen aber auch in anderen mathematischen Disziplinen eine große Rolle, hier
nur einige Hinweise:
• A.c.i. Systeme (algebraic completely integrable systems): A.c.i. Systeme sind spezielle Dynamische
Systeme, bei denen die abelschen Varietäten eine Rolle spielen. (vgl. [AMV]).
• Zahlentheorie: Beweis zum Satz von Fermat.
• Kryptographie, Fehlerkorrigierende Codes.
In diesem Zusammenhang wurde sogar ein Patent auf die Dissertation von S. Sessler vergeben
(vgl. [Se]). Ihre Idee war, endliche Gruppen mit hinreichend großem Primfaktor zu finden. Eine
Möglichkeit stellt die Gruppe der rationalen Punkte auf einer Prymvarietät dar.
Nicht zuletzt sind abelsche Varietäten aber auch wegen ihrer schönen Bilder im projektiven Raum
interessant:
3.8 Die abelsche Fläche vom Type (1, 4) in P3
Eine abelsche Fäche vom Typ (1, 4) wird birational auf eine Oktik, also eine Fläche vom Grad 8, in
P3 abgebildet. Diese Oktik ist eine Überlagerung der klassischen Kummerfläche. Diese ist bekannt für
ihre 16 Doppelpunkte, die auch in der Graphik zu erkennen sind (siehe [BLS] für eine ausführliche
Darstellung). Die folgenden beiden reellen Darstellungen dieser beiden Flächen wurden von Oliver Labs
(http://www.oliverlabs.net/) mit dem Programm Surf erstellt und mir freundlicherweise zur Verfügung
gestellt.
Abelsche Fläche vom Typ (1, 4)
Die Kummerfläche
25
4. Lösungen
Aufgabe 1.2.1:
Zeige, dass parallele Geraden in R2 einen gemeinsamen Fernpunkt haben.
Lösung: Jede Gerade in R2 kann durch eine Gleichung der Form Ax + By = C beschrieben
werden. Zwei Geraden G1 : A1 x + B1 y = C1 und G2 : A2 x + B2 y = C2 sind genau dann
parallel, wenn A1 B2 = B1 A2 . (Um das besser zu verstehen, multipliziere man die erste Geradengleichung mit B2 und die zweite mit B1 .) Der projektive Abschluss Gi wird durch die
homogene Gleichung Ai x1 + Bi x2 = Ci x0 gegeben. Die Fernpunkte von Gi , für i = 1, 2, sind
Gi ∩ {x0 = 0} = { (0 : x1 : x2 ) | Ai x1 + Bi x2 = 0} = {(0 : −Bi : Ai )}
für i = 1, 2.
Falls A2 6= 0, gilt
(0 : −B1 : A1 ) = (0 : −B1 A2 : A1 A2 ) = (0 : −A1 B2 : A1 A2 ) = (0 : −B2 : A2 ),
das heißt, die Fernpunkte stimmen überein. Insbesondere ist der Fernpunkt von Gi der Punkt
Ai
(0 : −Bi : Ai ) = (0 : 1 : − B
). Die dritte Koordinate in der zweiten Darstellung dieses
i
Ai
Punktes, also die Zahl − Bi , ist genau die Steigung der Geraden. Man kann also Fernpunkte
einer Geraden auch als Richtungen interpretieren.
Wenn A2 = 0 ist, muss B2 6= 0 sein und aus der Parallelitätseigenschaft folgt A1 = 0. Dann
haben beide Geraden (0 : 1 : 0) als Fernpunkt.
Aufgabe 1.2.2:
Zeige, dass sich zwei verschiedene Geraden in P2 genau in einem Punkt schneiden.
Lösung: Sind die Geraden parallel (im Affinen, also in R2 ), so schneiden sie sich auf der
∞-fernen Geraden, siehe Aufgabe 1.2.1. Ansonsten schneiden sie sich schon in R2 .
Aufgabe 1.2.3:
a b mit Determinante ad − bc 6= 0 definiert eine so genannte Projektivität
Eine 2 × 2-Matrix
c d
P = ac db : P1 7→ P1 , die auf den homogenen Koordinaten durch Multiplikation wirkt:
X0 aX0 +cX1
a b
Da
gilt
P (X0 : X1 ) = (aX0 + cX1 : bX0 + dX1 ).
c d
X1 = bX0 +dX1 ,
Finde die Projektivitäten, die die rationalen Funktionen a) x 7→ x + c, b) x 7→ c · x,
x
c) x 7→ − x1 , d) x 7→ 1 + x1 und e) x 7→ x−1
fortsetzen.
Lösung:
a) x 7→ x + c schreibt sich in homogenen Koordinaten (1 : x) 7→ (1 : x + c) und setzt sich zu
der Projektivität (X0 : X1 ) 7→ (X0 : X1 + cX0 ) fort. Die zugehörige Matrix ist P = 1c 10 .
1 .
b) P = 10 0c , denn P · x1 = c·x
x
1
0 1
1
c) P = −1
0 , denn P · x = −1 und (x : −1) = (1 : − x ).
x
d) P = 01 11 , denn P · x1 = 1+x
und (x : 1 + x) = (1 : x1 + 1).
1
1
x−1 und (x − 1 : x) = (1 : x ).
e) P = −1
x
0 1 , denn P · x =
x−1
26
Aufgabe 1.2.4:
Ein Fixpunkt einer Projektivität P : P1 7→ P1 ist ein Punkt p mit P (p) = p.
2
a) Bestimme die Fixpunkte von P = 12 −1
.
b) Zeige, dass eine nicht triviale Projektivität, also P 6= 10 01 , höchstens zwei Fixpunkte
haben kann.
c) Finde eine Projektivität des P1 mit Fixpunkt (1 : −1), welche die Punkte (0 : −1) und
(2 : 0) vertauscht.
Lösung:
√
5 : 2). Diese findet man folgendermaßen: Man löse zunächst
a) P hat die zwei Fixpunkte
(1±
X0
X0
2
=
λ
für eine Zahl λ 6= 0. Das dazu äquivalente Gleidie Gleichung 12 −1
X1
n X1
(1−λ)X0 +2X1 = 0
chungssystem lautet 2X0 −(1+λ)X1 = 0 . Mit dem Einsetzungsverfahren ergibt die zweite
(1−λ2 )+2 Gleichung X0 = 1+λ
X1 = 0.
2 X1 und Einsetzen in die erste Gleichung führt zu
2
X1 = 0 würde zu X0 = 0 führen, was aber bei homogenen Koordinaten nicht zulässig
√
2
)
ist. Also gilt (1−λ
+ 2 = 0, oder äquivalent λ = ± 5. Diese Lösungen, eingesetzt in die
2
√
zweite Gleichung, liefern nun: X0 = 1±2 5 X1 . Mit X1 = 2 folgt die Behauptung.
b) Die Fixpunkte einer Projektivität P = ac db entsprechen den Eigenvektoren der Matrix
X0 a b . Genauer: Es muss zunächst die Gleichung a b
0
in λ gelöst werden.
=λ X
c d
c
d
X
X
1
1
X0 a−λ b
0
. Da (X0 , X1 ) 6= (0, 0), gibt es nur
Die Gleichung ist äquivalent zu
X1 =
c d−λ
0
b
eine Lösung, wenn die Determinante det a−λ
=
0.
Das ist aber nun eine quadratische
c d−λ
Gleichung, die bis zu zwei Lösungen λ1/2 , die so genannten Eigenwerte von P , haben kann.
Zu den Eigenwerten gibt es je einen Fixpunkt. Eine 2 × 2-Matrix kann also höchsten zwei
Eigenvektoren haben.
c) P = 01 10 , beachte, dass (0 : −1) = (0 : 1) und (2 : 0) = (1 : 0).
Aufgabe 1.2.5:
Für Punkte A = (a0 : a1 : a2 ), B = (b0 : b1 : b2 ) und C = (c0 : c1 : c2 ) ∈ P2 sind äquivalent:
i) A, B und C sind kollinear.
ii) Die Geraden GA : a0 xx + a1 x1 + a2 x2 = 0, GB : b0 xx + b1 x1 + b2 x2 = 0 und GC :
c0 xx + c1 x1 + c2 x2 = 0 schneiden sich in einem Punkt.
a0 a1 a2 iii) det b0 b1 b2 = 0
c0 c1 c2
Lösung: Es gelte ii) und sei (α : β : γ) der gemeinsame Schnittpunkt. Dann genügen
(a0 , a1 , a2 ), (b0 , b1 , b2 ) und (c0 , c1 , c2 ) der Gleichung αx0 + βx1 + γx2 = 0. Also liegen
A, B und C auf der Geraden mit der Gleichung αx0 + βx1 + γx2 = 0 und
es gilt
i). Schließlich
ist (α, β, γ) eine nicht triviale Lösung des Gleichungssystems
iii).
a0 a1 a2
b0 b1 b2
c0 c1 c2
x0
x1
x2
= 0, also folgt
27
Aufgabe 1.2.6:
Zwei Punkte a, b ∈ Rn (hier können wir einfach n = 1 oder 2 annehmen, es geht aber auch
allgemeiner) definieren eine Gerade G := ab in R2 . Ein Punkt x auf dieser Geraden lässt sich
folgendermaßen schreiben
x = a + t(b − a) = (1 − t)a + tb
mit einem eindeutig bestimmten t ∈ R.
Das Teilverhältnis von x bezüglich a und b ist definiert durch
t
.
t−1
T V (x ; a, b) :=
Falls t = 1 oder äquivalent x = b, so definiert man T V (b ; a, b) = ∞.
a) Bezeichne mit ∞G den ∞-fernen Punkt der Geraden G. Zeige, dass sich T V zu einer
Bijektion T V : G ∪ {∞G } → P1 fortsetzen lässt.
b) Zeige, dass
1
,
T V (x ; a, b)
T V (x ; a, b)
T V (a ; x, b) =
.
T V (x ; a, b) − 1
T V (b ; a, x) = 1 − T V (x ; a, b) ,
T V (a ; b, x) = 1 −
T V (x ; b, a) =
1
,
T V (x ; a, b)
c) Zeige, dass für drei paarweise verschiedene Punkte x, a, b ∈ R gilt
T V (x ; a, b) · T V (a ; b, x) · T V (b ; x, a) = −1 .
d) Zeige, dass für vier paarweise verschiedene Punkte x, a, b, c ∈ R gilt
T V (x ; a, b) · T V (x ; b, c) · T V (x ; c, a) = 1 .
Lösung:
a) Hier ist ∞G der unendlich-ferne Punkt der Geraden G. Dann setzt man
T V (∞G ; a, b) := (1 : 1),
T V (b; a, b) := (0 : 1),
T V (x; a, b) := (t − 1 : t).
b) Aus b = (1 − 1t )a +
1
t
folgt T V (b ; a, x) =
1
t
1
t −1
=
1
t
=1−
Aus x = (1 − (1 − t))b + (1 − t)a folgt T V (x ; b, a) =
Aus a = (1 −
1
1−t )b
+
1
1−t x
folgt T V (a ; b, x) =
Aus a = (1 −
t
t−1 )x
+
t
t−1 b
folgt T V (a ; x, b) =
1
1−t
1
1−t −1
t
t−1
t
t−1 −1
t−1
t
1−t
1−t−1
=
= 1 − T V (x ; a, b).
t−1
t
=
=
1
t
=
T V (x ;a,b)
T V (x ;a,b)−1 .
=1−
t−1
t
1
T V (x ;a,b) .
=1−
1
T V (x ;a,b) .
c) Mit b) gilt:
T V (x ; a, b) · T V (a ; b, x) · T V (b ; x, a) = T V (x ; a, b) · 1 −
= T V (x ; a, b) · 1 −
1
1
·
T V (x ; a, b) T V (b ; a, x)
1
1
·
= −1
T V (x ; a, b) 1 − T V (x ; a, b)
d) Sei x = (1 − s)b + sc. Auflösen nach b liefert b = x−sc
1−s . Einsetzen in x = (1 − t)a + tb ergibt
(1−s)(1−t)
(1−s)(1−t)
x = 1 − 1−s−t
c + 1−s−t a und es folgt:
T V (x ; a, b) · T V (x ; b, c) · T V (x ; c, a) =
t
s
·
·
t−1 s−t
(1−s)(1−t)
1−s−t
(1−s)(1−t)
−
1−s−t
=1
1
28
Aufgabe 1.3.7:
Berechne die Schnittpunkte und ihre Vielfachheiten von a) der Ellipse
b) der Hyperbel x1 x2 = x20 mit der Geraden {x0 = 0}.
x21
a2
+
x22
b2
= x20 und
Lösung:
x2
x2
a) Einsetzen von x0 = 0 in die Gleichung der Ellipse liefert die Gleichung a21 + b22 = 0. Diese
hat nur die Lösung x1 = x2 = 0. Da aber mindestens eine homogene Koordinate von Null
verschieden sein muss, gibt es keinen Schnittpunkt.
b) Einsetzen von x0 = 0 in die Gleichung der Hyperbel liefert die Gleichung x1 x2 = 0 und
diese wird durch x1 oder x2 = 0 gelöst. Somit sind die gesuchten Schnittpunkte (0 : 0 : 1)
und (0 : 1 : 0).
Aufgabe 1.3.8:
a11
Sei P = aa21
31
a12 a13
a22 a23
a32 a33
2
eine 3 × 3 - Matrix mit Determinante det P 6= 0. Diese definiert eine
Projektivität P : P → P2 , die auf den homogenen Koordinaten durch Multiplikation mit der
Matrix P wirkt: Da
a11 a12 a13 x0 a11 x0 +a12 x1 +a13 x2 a21 a22 a23
x1
= a21 x0 +a22 x1 +a23 x2 ,
a a a
x
31
32
33
a31 x0 +a32 x1 +a33 x2
2
gilt
P (x0 : x1 : x2 ) = (a11 x0 + a12 x1 + a13 x2 : a21 x0 + a22 x1 + a23 x2 : a31 x0 + a32 x1 + a33 x2 ).
Zwei Quadriken Q1 = 0 und Q2 = 0 in P2 heißen projektiv äquivalent, wenn es eine Projektivität P mit
Q1 P (x0 : x1 : x2 ) = Q2 (x0 : x1 : x2 )
gibt. Zeige, dass die Quadriken QParabel (x0 : x1 : x2 ) = x0 x2 − x21 = 0, QEllipse (x0 : x1 :
x2 ) =
x21
a2
+
x22
b2
− x20 = 0 und QHyperbel (x0 : x1 : x2 ) = x1 x2 − x20 = 0 projektiv äquivalent sind.
Lösung: Sei P1 =
0 1 0
100
001
. Dann gilt QParabel P1 (x0 : x1 : x2 ) =
P2 (x0 : x1 : x2 ) = −QHyperbel (x0 : x1 : x2 ).
und P2 =
QHyperbel (x0 : x1 : x2 ) und QEllipse
0 21 12
a
0 a
2 −2
b 0 0
Aufgabe 1.3.9:
Untersuche, ob die Quadriken Q1 (x0 : x1 : x2 ) = x20 − x21 − x22 = 0 und Q2 (x0 : x1 : x2 ) =
x21 − x22 = 0 projektiv äquivalent sind.
Lösung: Wegen Q2 = x21 − x22 = (x1 + x2 )(x1 − x2 ) = 0 besteht Q2 aus den sich schneidenden
Geraden x1 + x2 = 0 und x1 − x2 = 0. Wären Q1 und Q2 projektiv äquivalent, so müsste auch
Q1 eine Gerade enthalten. Das ist aber nicht der Fall, denn Q1 = 0 ist die homogenisierte
Gleichung des Einheitskreises.
29
Aufgabe 2.1.10:
Eine Funktion f (z) := αz+β
γz+δ mit komplexen Zahlen α, β, γ und δ mit αδ − βγ 6= 0 heißt
Möbius-Transformation (siehe auch [M4]). Der Definitionsbereich von f ist Df = C\{− γδ }
und der Wertebereich ist Wf = C\{ αγ } (falls γ 6= 0), andernfalls Df = C und Wf = C. f kann
zu einer bijektiven Abbildung f : P1 → P1 fortgesetzt werden, indem man f (γ : −δ) := (0 :
1) und f (0 : 1) := (γ : α) setzt. Zeige, dass die Möbius-Transformation f eine Projektivität
ist
Lösung: Für Z0 6= 0 und z =
Z1
Z0
gilt
f (Z0 : Z1 ) = f (1 : z) = 1 : f (z) = 1 : αz+β
γz+δ = (γz + δ : αz + β) = (γZ1 + δZ0 : αZ1 + βZ0 ).
γZ1 +δZ0
δ γ
Z0
Weil βδ αγ
=
und
da
nach
Vorraussetzung
det
= αδ − βγ 6= 0,
Z1
αZ1 +βZ0
β α
entspricht f der Projektivität mit der Matrix βδ αγ .
Aufgabe 2.1.11:
Sind x, y, a, b komplexe Zahlen, so ist ihr Doppelverhältnis definiert durch
DV (x, y, a, b) :=
a) Zeige, dass DV (x, y, a, b) =
(x−a)
(x−b)
:
(y−a)
(y−b)
=
(x−a)(y−b)
(x−b)(y−a)
.
T V (x;a,b)
T V (y;a,b) .
b) Das Doppelverhältnis lässt sich zu einer Abbildung DV : P1 → P1 fortsetzen.
c) Zeige, dass das Doppelverhältnis unter Möbius-Transformationen invariant ist.
Lösung:
a) Seien x = a + t(b − a) und y = a + s(b − a). Dann gilt
x − a = t(b − a)
und
x − b = (b − a)(t − 1)
y − a = s(b − a)
und
y − b = (b − a)(s − 1)
(x − a)(y − b)
t(b − a)(b − a)(s − 1)
⇒ DV (x, y, a, b) =
=
(x − b)(y − a)
(b − a)(t − 1)s(b − a)
t
s−1
T V (x; a, b)
=
·
=
.
t−1
s
T V (y; a, b)
b) Für x = (x0 : x1 ), y = (y0 : y1 ), a = (a0 : a1 ) und b = (b0 : b1 ) setze
det xx01 aa01 · det yy01 bb01
.
DV (x, y, a, b) =
det xx01 bb01 · det yy01 aa01
Dann gilt DV (1 : x), (1 : y), (1 : a), (1 : b) = DV (x, y, a, b).
c) Das ist mit b) einfacher zu zeigen: Ist P = βδ αγ die Matrix einer Möbius-Transformation,
so gilt wegen des Determinanten Multiplikationssatzes
det P · xx01 aa01 · det P · yy01 bb01
DV (P (x), P (y), P (a), P (b)) =
det P · xx10 bb10 · det P · yy01 aa01
det xx01 aa01 · det yy01 bb01
= DV (x, y, a, b).
=
det xx01 bb01 · det yy01 aa01
30
Aufgabe 2.1.12:
Zu je drei verschiedenen komplexen Zahlen z1 , z2 , z3 und v1 , v2 , v3 gibt es genau eine MöbiusTransformation f mit f (zi ) = vi für i = 1, 2, 3.
(z−z2 )·(z1 −z3 )
(z−z3 )·(z1 −z2 ) bildet z1 , z2 , z3 auf 1, 0, ∞ (in der
2 )·(v1 −v3 )
für g(z) := (z−v
(z−v3 )·(v1 −v2 ) . Nun ist die Verkettung
Lösung: Die Möbius-Transformation f (z) :=
angezeigten Reihenfolge) ab. Analoges gilt
g −1 ◦ f , also die Funktion g −1 f (z) , die gesuchte Möbius-Transformation.
Aufgabe 2.1.13:
Zwei Quadrupel x, y, a, b und x0 , y 0 , a0 , b0 komplexer Zahlen sind genau dann projektiv äquivalent, wenn ihre Doppelverhältnisse gleich sind.
Lösung:
Die Richtung 00 ⇒ 00 folgt aus Aufgabe 2.1.11 c). Für 00 ⇐ 00 sei f (z) die MöbiusTransformation, die (nach Aufgabe 2.1.12) y, a, b auf y 0 , a0 , b0 abbildet. Es bleibt zu zeigen,
dass f (x) = x0 ist. Aus
DV (x0 , y 0 , a0 , b0 ) = DV (x, y, a, b) = DV (f (x), f (y), f (a), f (b)) = DV (f (x), y 0 , a0 , b0 )
folgt mit Aufgabe 2.1.11 a), dass
T V (f (x); a0 , b0 )
T V (x0 ; a0 , b0 )
0 0 0 0
0 0 0
=
DV
(x
,
y
,
a
,
b
)
=
DV
(f
(x),
y
,
a
,
b
)
=
T V (y 0 ; a0 , b0 )
T V (y 0 ; a0 , b0 )
und äquivalent
T V (x0 ; a0 , b0 ) = T V (f (x); a0 , b0 ).
Ein Punkt ist aber durch sein Teilverhältnis eindeutig festgelegt, somit folgt dass f (x) = x0 .
Aufgabe 2.1.14:
Finde die Möbius-Transformation f , die die Punkte 1, i, −1 auf 0, 1, ∞ in der gegebenen
Reihenfolge abbildet.
Lösung: f (z) =
z−1
iz+i
Aufgabe 2.1.15:
Seien x, y, a, b paarweise verschiedene komplexe Zahlen. Man sagt, das Punktepaar x, y trennt
die Punkte a, b harmonisch, wenn DV (x, y, a, b) = −1. Zeige, das x, y das Paar a, b genau
dann harmonisch trennt, wenn es eine Möbius-Transformation gibt, die a, b fixiert und x, y
vertauscht.
Lösung: Nach Aufgabe 2.1.11 a) gilt
T V (y; a, b)
DV (y, x, a, b) =
=
T V (x; a, b)
T V (x; a, b)
T V (y; a, b)
−1
= DV (x, y, a, b)
−1
.
Gilt nun DV (x, y, a, b) = −1, so ist DV (y, x, a, b) = DV (x, y, a, b) und es gibt nach Aufgabe 2.1.13 eine Projektivität, die a, b fixiert und x, y vertauscht. Umgekehrt gibt es eine
−1
Projektivität, die a, b fixiert und x, y vertauscht, so gilt DV (x, y, a, b)
= DV (y, x, a, b) =
2
DV (x, y, a, b). Aber dann muss DV (x, y, a, b) = 1 sein. Wäre TT VV (x;a,b)
=
DV (x, y, a, b) =
(y;a,b)
1, so müsste wegen der Eindeutigkeit des Teilverhältnisses x = y sein, ein Widerspruch zur
Voraussetzung. Also gilt DV (x, y, a, b) = −1.
31
Aufgabe 2.2.16:
Finde die Koordinatentransformation, die die allgemeine Gleichung y 2 = az 3 + bz 2 + cz + d
einer elliptischen Kurve auf die Weierstrasssche Normalform bringt.
Lösung: (z, y) 7→ (z −
b
3a , y)
Aufgabe 2.2.17:
Zeige, dass der projektive Abschluss der affinen Kubik K : y = x3 − x geometrisch
zur Neilschen Parabel mit der affinen Gleichung y 2 = x3 äquivalent ist (siehe auch
Aufgabe 2.5.20) .
Lösung: Die homogene Gleichung der KubikK ist x20 x2 = x31 − x20 x1 oder äquivalent
0 0 1
x20 (x2 + x1 ) = x31 . Unter der Projektivität P = 0 1 0 : (x0 : x1 : x2 ) 7→ (x2 : x1 : x0 − x1 )
1 −1 0
geht K in die Gleichung x22 x0 = x31 über.
Aufgabe 2.5.18:
Beweise die Funktionaleigenschaften (12) und (13) der Riemannschen Thetafunktion ϑ. Hinweis: Benutze die Reihendarstellung von ϑ.
Lösung:
ϑ(v + n1 z + n2 ) =
X
ekπi
kz+2(v+n1 z+n2 )
k∈Z
=
X
eπi
[k2 +2kn1 ]z+2kv+2kn2
eπi
[k2 +2kn1 ]z+2kv
k∈Z
=
X
(weil eπi2kn2 = 1)
k∈Z
=
X
e
πi [(k+n1 )2 −n21 ]z+[2(k+n1 )−2n1 ]v
k∈Z
=
X
eπi
[k2 −n21 ]z+[2k−2n1 ]v
(ersetze in der Summe k durch k − n1 )
k∈Z
2
= e−πi(n1 z+2n1 v)
X
eπi
k2 z+2kv
2
= e−πi(n1 z+2n1 v) ϑ(v)
k∈Z
Aufgabe 2.5.19:
Beweise die Funktionaleigenschaft (14) der Thetafunktionen ϑ
c
3 .
0
Lösung: Vollkommen analog wie der Beweis für ϑ in Aufgabe 2.5.18.
32
Aufgabe 2.5.20:
Bestimme die affine und homogene Gleichung der Bildkurve der Abbildung ϕ1 : P1 → P2 mit
(Z0 : Z1 ) 7→ (Z03 : Z0 Z12 : Z13 ). Um welche Kurve handelt es sich und was sind die ∞-fernen
Punkte? Zeichne die affine Kurve, was fällt auf?
y
Lösung: Es handelt sich um die Neilsche Parabel mit der
homogenen Gleichung z0 z22 = z13 (bzw. affin y 2 = x3 ). Der
∞-ferne Punkt ist (0 : 0 : 1) und hat die Vielfachheit 3. Sie
hat in (0, 0) eine Spitze, das ist eine Singularität. Damit ist
die Neilsche Parabel eine singuläre ebene Kurve vom Grad 3.
Dass heißt insbesondere, dass die Neilsche Parabel keine elliptische Kurve ist.
x
Aufgabe 2.5.21:
Bestimme die affine und homogene Gleichung der Bildkurve der Abbildung ϕ2 : P1 → P2 mit
(Z0 : Z1 ) 7→ (Z03 : Z0 Z12 − Z03 : Z13 − Z02 Z1 ). Um welche Kurve handelt es sich und was sind
die ∞-fernen Punkte? Zeichne die affine Kurve, was fällt auf?
y
Lösung: ϕ1 (P1 ) hat die homogene Gleichung z0 z22 = z13 + z0 z12
(bzw. affin y 2 = x3 + x2 ). Der ∞-ferne Punkt ist (0 : 0 : 1) und
hat die Vielfachheit 3. Sie hat in (0, 0) einen Doppelpunkt, also
eine Singularität. Da Doppelpunkte im Englischen Node heißen, wird diese Kurve auch Nodale Kubik oder Newtonscher
Knoten genannt. Auch Nodale Kubiken sind als singuläre ebene Kurven vom Grad 3 keine elliptischen Kurven.
x
Aufgabe 2.6.22:
Θ
(0)
(0,0),1
Berechne die Schnittpunkte der elliptischen Kurve E : z03 + z13 + z23 = 3 Θ(0,6),1
(0) z0 z1 z2 mit
der ∞-fernen Geraden z0 = 0.
Lösung: Ersetzt man z0 = 0 in der Gleichung von E, so erhält man
z13 +z23= 0.
√ die Gleichung
√
1
1
3
3
Diese zerlegt sich in Linearfaktoren z1 +z2 = (z1 +z2 ) z1 − 2 (1+ 3i)z2 z1 − 2 (1− 3i)z2 = 0.
√
√
Somit sind P1 = (0 : −1 : 1), P2 = (0 : 12 (1 + 3i) : 1) und P3 = (0 : 12 (1 + 3i) : 1) die
∞-fernen Punkte von E.
Aufgabe 2.7.23:
Seien u und v ∈ C und n ∈ Zz + Z3. Zeige, dass in E = C/(Zz + Z3) gilt:
a) u = v genau dann, wenn u − v ∈ Zz + Z3.
b) n = 0.
c) u + v = u + v.
Lösung:
a) u = u + Zz + Z3 und v = v + Zz + Z3. Also u + Zz + Z3 = v + Zz + Z3 genau dann, wenn
u − v ∈ Zz + Z3.
b) n = n + Zz + Z3 = Zz + Z3 = 0, da n ∈ Zz + Z3.
c) u + v = u + Zz + Z3 + v + Zz + Z3 = u + v + Zz + Z3 = u + v.
33
Literatur
[AMV]
M.Adler, P. van Moerbeke, P. Vanhaecke, Algebraic Integrability, Painlevé Geometry and Lie
Algebras,Springer, Ergebnisse der Mathematik und ihrer Grenzgebiete Vol 47 (2004)
[ACGH] E. Arbarello, M. Cornalba, P.A. Griffiths, J. Harris, Geometry of Algebraic Curves, Vol I,
Springer, Grundlehren 267 (1985)
[B]
A. Beutelspacher, Lineare Algebra, Mathematik für Studienanfänger, Vieweg & Sohn Verlag
(2003)
[BL1]
Ch. Birkenhake, H. Lange, Cubic theta relations, Jour. reine angew. Math. 407, 167-177 (1990)
[BL2]
Ch. Birkenhake, H. Lange, Complex Abelian Varieties, Springer, Grundlehren 302 (2004)
[BLS]
Ch. Birkenhake, H. Lange, D. v. Straten, Abelian surfaces of type (1,4). Math. Ann. 285,
625-646 (1989)
[F]
G. Fischer, Ebene algebraische Kurven, Vieweg Studium (1994)
[FB]
E. Freitag, R. Busam, Funktionentheorie 1, dritte Auflage, Springer (2000)
[GH]
Ph. Griffiths, J. Harris, Principles of Algebraic Geometry, JohnWiley & Sons (1978)
[Ha]
R. Hartshorne, Algebraic Geometry, Grad. Texts Math. 52, Springer (1977)
[Hu]
K. Hulek, Elementare Algebraische Geometrie, Vieweg Studium - Aufbaukurs Mathematik ,
vieweg (2000)
[K]
A. Krazer, Lehrbuch der Thetafunktionen. Teubner, Leipzig (1903)
[M1]
K. Meyer, Komplexe Zahlen als Beispiel für eine Binnendifferenzierung, Mathematikinformation Nr. 50
[M2]
K. Meyer, Schüler untersuchen die Geometrie von Billardtischen, Mathematikinformation
Nr. 51
[M3]
K. Meyer, Stereographische
www.bfmathematik.info/ (1997)
[M4]
K. Meyer, Kreisgeometrie, Mathematikinformation Nr. 26, 3-25, www.bfmathematik.info/
(1996)
[SS]
C.J. Scriba, P. Schreiber, 5000 Jahre Geometrie, Springer (2005)
[Se]
S. Seßler, Nicht prinzipal polarisierte Varietäten für die Kryptographie, Dissertation, Erlangen
(2007)
[Si]
J. Silverman, The Arithmetic of Elliptic Curves, Grad. Texts Math. 106, Springer (1985)
Projektion,
Anschrift des Autors:
Prof. Dr. Christina Birkenhake
Department Mathematik - Universität Erlangen-Nürnberg
Bismarckstraße 1 12
D-91054 Erlangen
Germany
[email protected]
http://christina.birkenhake.net
Eingereicht am 15. April 2008
Mathematikinformation
Nr.
29,
3-36,