4.5 Güterangebot und Faktornachfrage im Monopolfall

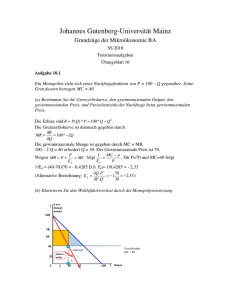
Mikroökonomik
4.5 Güterangebot und Faktornachfrage im Monopolfall
Verhaltensannahme: Unternehmen versuchen, möglichst hohe Gewinne zu erwirtschaften.
Formale Modellierung:
max p( y ) y − w1x1 − w2 x2 u.d.N. f ( x1, x2 ) ≥ y
x, y
Die Inputpreise w1 und w2 sind in diesem Abschnitt weiterhin exogen gegeben. Der Outputpreis ist jedoch nicht als aus
Unternehmenssicht unveränderlich angenommen.
p ( y ) ist die Preisabsatzfunktion, was mathematisch der Umkehrfunktion der Nachfragefunktion entspricht:
y = d ( p) ⇔ d = p( y )
Dabei wird unterstellt, dass sich durch das Verhalten des Monopolisten die anderen Nachfragedeterminanten (Preise der anderen Güter,
Einkommen) nicht ändern.
Zusammenhang zur Darstellung in 3.5!
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
1
Mikroökonomik
Lagrangeansatz: : L( y, x1, x2 , λ ) = p ( y ) y − w1x1 − w2 x2 + λ ( f ( x1, x2 ) − y )
∂L
= p( y ) + p′( y ) y − λ = 0 ⇔ λ = p( y ) + p′( y ) y
∂y
(1)
f ( x1, x2 )
∂L
∂f
= − w1 + λ
= 0 ⇔ w1 = λα x1α −1x2β = λα
x1
∂x1
∂x1
(2)
f ( x1, x2 )
∂L
∂f
= − w2 + λ
= 0 ⇔ w2 = λβ x1α x2β −1 = λβ
x2
∂x2
∂x2
(3)
f ( x1, x2 ) = y ⇔ x1α x2β = y
(4)
Man beachte, dass sich (2) bis (4) gegenüber „Preisnehmerverhalten“ nicht unterscheiden. Aus diesen Gleichungen folgt, dass die Wahl
der Inputs Kosten minimierend erfolgen wird. Daher können wir auch das Gewinnmaximierungsproblem eines Monopolisten stark
vereinfachen:
max p( y ) y − C ( y )
y
p( y ) y ist offensichtlich der Erlös. Eine marginale Erhöhung der Absatzmenge ändert den Erlös um
MR( y ) = p( y ) + p′( y ) y , den Grenzerlös.
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
2
Mikroökonomik
Dann lautet die Bedingung erster Ordnung: p( y ) + p′( y ) y = MC ( y ) ⇔ Grenzerlös = Grenzkosten
Ein Monopolist wählt seine Gewinn maximierende Absatzmenge so, dass der Grenzerlös den Grenzkosten entspricht. (Beziehung zu
Preis = Grenzkosten?).
Da die Steigung der Preisabsatzfunktion (Nachfragekurve) negativ angenommen wird, ist p’ negativ. Folglich wird im
Gewinnmaximum der Preis oberhalb der Grenzkosten liegen.
Beachte: im Monopolfall gibt es keine Angebotsfunktion! An den Faktornachfragen ändert sich nichts wesentliches gegenüber dem
„Preisnehmerfall“.
Graphische Veranschaulichung:
p
p(y)
pm
MC
MR
y
ym
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
3
Mikroökonomik
Für einen Monopolisten macht es keinen Unterschied, ob er die Absatzmenge festlegt und dann den Preis fordert, bei dem er diese
Menge absetzen kann, oder ob er erst den Preis festlegt und dann die Absatzmenge produziert, die zu diesem Preis nachgefragt wird.
Daher können wir das Gewinnmaximierungsproblem eines Monopolisten auch wie folgt formulieren:
max pd ( p) − C (d ( p))
p
Die Bedingungen erster Ordnung zu diesem Problem lauten: d ( p ) + pd ′( p) − MC (d ( p))d ′( p ) = 0
Die ersten beiden Summanden sind der Grenzerlös einer marginalen Preiserhöhung. Normalerweise wird der Begriff „Grenzerlös“ auf
eine Mengenerhöhung bezogen!
Umstellung der letzten Gleichung ergibt über
p − MC (d ( p )) = −
d ( p)
d ′( p )
p − MC (d ( p))
d ( p) 1
1
=−
=
p
d ′( p) p ε ( p)
Die linke Seite dieser Gleichung heißt Lerner Index (für die Marktmacht). ε (p) ist offenbar die Preiselastizität der Nachfrage.
Die Gleichung hat die technische Implikation, dass ein Monopolist den Preis immer so wählt, dass er in dem Bereich der
Nachfragefunktion liegt, bei dem ε (p) > 1 gilt (im elastischen Bereich der Nachfrage).
Die Gleichung hat die ökonomisch bedeutsame Implikation, dass ein Monopolist einen höheren Preisspielraum hat, wenn die
Preiselastizität niedrig ist.
Cost plus!
Prof. Norbert Schulz, Ph.D., Lehrstuhl für Strategie und Wettbewerb (Industrieökonomik)
4