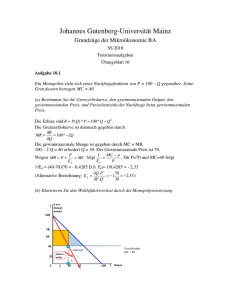
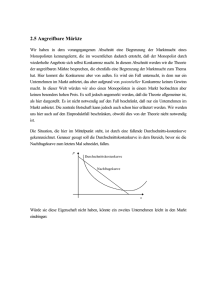
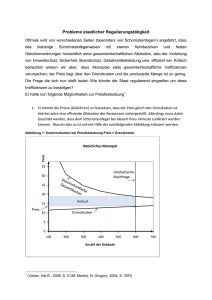
N 2 2θ 1 t 0) θ ,NC( t π N 2 2θ 1 t 0)

Prof. Dr. Christian Wey
TU-Berlin
Fachgebiet Volkswirtschaftslehre
Insbes. Netzwerk- und IuK-Ökonomie
Musterlösung zur Klausur
Telekommunikationsökonomik
WS 2005/06
27.02.06; 10-11 Uhr
Aufgabe 1.
1.
Der Regulierer maximiert unter vollständiger Information.
Für den L-Typ ergibt sich:
max S = N L − t L
N
s.t. π L = t L − C( N L , θ L) ≥ 0 ⇔ t L ≥
S= N−
1
2θ L
NL
1
2θL
NL
2
2
FOC :
1
1 − NL = 0
θL
*
NL = θL
*
N H = θ H entsprechend
Die Partizipationsbedingungen müssen erfüllt sein :
1
2
π L = t L − C( N L , θL ) ≥ 0 ⇔ t L ≥
NL
2θ L
1
2
π H = t H − C( N H , θ H ) ≥ 0 ⇔ t H ≥
NH
2θH
1
⇒ t*L = θ L
2
1
⇒ t*H = θ H
2
Die erstbesten Netzgrößen sind N*L=θL und N*H=θH.
Die erstbesten Transfers sind dann t*L=(1/2) θL und t*H=(1/2) θH.
2a)
Die „incentive compatibility“ Bedingungen (IC) sind
t L − (1/(2 θ L)) N L ≥ t H − (1/(2 θL )) N H
2
2
t H − (1/(2 θ H )) N H ≥ t L − (1/(2 θ H)) N L
2
2
(1)
(2)
und die „participation“ Bedingungen (PC) sind
2
t L − (1/(2 θL )) N L ≥ 0
2
t H − (1/(2 θ H)) N H ≥ 0
2b)
(3)
(4)
Aufsummieren der IC-Bedingungen ergibt:
 1
1  2
−

(N H − N 2L ) ≥ 0
2
2
θH 
 θL
Der erste Term ist negativ. Daraus folgt, dass NH < NL sein muss.
2c)
(1) und (2) ergibt:
(1/(2 θ H))( N 2L − N2H ) ≥ t L − t H ≥ (1/(2 θ L ))( N 2L − N 2H)
Wegen NH<NL und θL> θH folgt, dass positive Transfers mit tL ≥ tH existieren,
die die Anreizbedingungen erfüllen.
2d)
(1) und (4) binden. Bei Nullgewinn des H-Typs ergibt (4): t H = (1/2 θH ) N 2H
Einsetzen in (1) führt zur Informationsrente vom L-Typ (damit dieser nicht den
H-Typ nachahmt)
1  2
 1
2
−
 N H
t L − (1/2 θ L) N L ≥ 
 2 θH 2 θL 
2
πL ≥ ∆ NH
Es gilt also π L ≥ ∆ N 2H und π H = 0 .
Das Maximierungsproblem des Regulierers lautet:
υ( N L − t L ) + (1 − υ)( N H − t H )
oder
υ( N L − (1/(2 θ L)) N2L ) + (1 − υ)( N H − (1/(2 θ H)) N 2H) − υ π L − (1 − υ) π H
oder
υ( N L − (1/(2 θ L)) N2L ) + (1 − υ)( N H − (1/(2 θ H)) N 2H) − υ∆ N2H
Bedingung erster Ordnung für NL:
NL** = θL
**
und für NH: N H = θ H
1− υ
< θH
(1 − υ) + 2υ ∆ θ H
Entsprechend können die Gewinne dargestellt werden:
π L = t L − (1/(2 θ L)) NL = ∆ N H
2
π H = t H − (1/(2 θH )) NH = 0
2
2
Einsetzen von NH** und Auflösen nach tL, tH ergibt die optimalen Transfers.
Wir erhalten also, dass das effiziente L-Unternehmen die effiziente Netzgröße
anbietet und eine positive Informationsrente erhält. Hingegen produziert das
ineffiziente H-Unternehmen eine kleinere als die effiziente Menge und macht
keinen Gewinn.
Die „Verzerrung“ der Menge des ineffizienten Unternehmenstyps steigt in ∆.
Sowohl NH als auch die Informationsrente fällt in v, also mit einer
anwachsenden Wahrscheinlichkeit des L-Typs.
2e)
Würde unterstellt werden, dass die Gewinne des Unternehmens wenigstens
anteilig (etwa mit α gewichtet) in die Zeilfunktion des Regulierers eingehen, so
ergibt sich für die optimale Menge des H-Typs
**
NH = θH
1− υ
< θH
(1 − υ) + (1 − α )2υ∆ θ H
so dass für α=1 Unternehmen H ebenfalls die effiziente Menge produzieren
würde.
Aufgabe 2.
1.
Die Ramsey-Formel für den Fall unabhängiger Nachfragen lautet:
∆C
λ 1
∆ xi
=
⋅
1+ λ ε
pi
pi −
Ramsey-Preise
- maximieren die soziale Wohlfahrt unter dem Gesichtspunkt, dass das
Unternehmen keine Verluste schreibt.
- berücksichtigen, dass die Grundregel „Preis gleich Grenzkosten“ (= firstbest Preise) aufgrund bestehender Fixkosten suboptimal sein kann
- sind second-best Preise
Die Preisstruktur entspricht der eines unregulierten Monopolisten, wegen λ > 0
fallen die Preisaufschläge auf die Grenzkosten jedoch geringer aus.
Produkte mit einer geringen Preiselastizität der Nachfrage erhalten höhere
Preisaufschläge als Produkte, die eine hohe Preiselastizität aufweisen.
Bei Substituten:
Aufgrund von Kannibalisierung mindern Preissenkungen den Gewinn. Die
Preise werden hoch gesetzt.
Bei Komplementen:
Preissenkungen an einem Gut erhöhen den Verkauf von anderen Gütern.
Quersubventionen sind möglich; die Preise sinken und können sogar unter die
Grenzkosten fallen.
2.
„Contestable Markets“
Die Theorie der bestreitbaren Märkte besagt, dass ein Monopolist durch
Androhung potentiellen Wettbewerbs in seiner Preissetzung diszipliniert
werden kann.
Alle Marktteilnehmer sind symmetrisch (Kostenstruktur, Informationsstruktur,
Marktzugang…).
3 Annahmen beschreiben einen vollkommen bestreitbaren Markt.
a)
freier Marktzutritt
b)
kostenloser Marktaustritt (keine „sunk costs“)
c)
Die Zeitverzögerung beim Marktzutritt (entry lag) ist kürzer als die
Zeitverzögerung bei der Preisanpassung (price adjustment lag)
Hit-and-run-Strategie durch Entrant möglich. Entrant tritt in den Markt,
unterbietet den Preis des Monopolisten und greift in kurzer Zeit den Markt ab.
Um sich nicht der Gefahr potentiellen Wettbewerbs auszusetzen, hat der
Monopolist den Anreiz marktzutrittsresistente Preise zu setzen, so dass
- er keinen Verlust erwirtschaftet und gleichzeitig
- es sich für keinen potentiellen Wettbewerber lohnt in den Markt zu treten.
Aus der Annahme, dass alle Unternehmen mit gleicher Effizienz produzieren
können, folgt, dass der Monopolist zu minimalen Kosten produziert.
„Weak Invisible Hand Theorem“
Behauptung: Ramsey-Preise sind marktzutrittsresistent, wenn
a) die Kostenfunktion fallende Strahlendurchschnittskosten aufweist
b) die Eigenschaft der Querstrahlkonvexität vorliegt und
c) die Güter schwache Substitute sind
Die Androhung von potentiellem Wettbewerb bewegt den Monopolisten dazu,
marktzutrittsresistente Ramsey-Preise zu setzen, wodurch eine
wohlfahrtsoptimale second-best Lösung erreicht wird.
Diese Theorie wurde scharf kritisiert wegen der starken Annahmen, die
unrealistisch erscheinen. Zudem existieren i.d.R. mehrere Preis-MengenKombinationen, die marktzutrittsresistent sind. Der Monopolist wird daher
auch bei Androhung von potentiellem Wettbewerb nicht unbedingt RamseyPreise wählen und somit von einer second-best-Lösung abweichen.
3.
ECPR-Regel
Herleitung aus dem Burden-Test:
a-2c0 ≥ p1 – (2c0 + c1)
a ≥ p1-c1
Der Zugewinn, wenn der Entrant die Leistung bereitstellt, soll höher sein als
der Verlust, den der Monopolisten dabei erleidet.
ECPR-Regel:
a ≤ p1 – c1
Der Zugangspreis soll die Opportunitätskosten des Monopolisten
(entgangener Gewinn) nicht übersteigen.
Nur kosteneffiziente Unternehmen treten in den Markt (c2 < c1).
ECPR-Regel wirkt sich nicht auf den Gewinn des Monopolisten aus.
Dadurch hat der Monopolist keinen Anreiz sich einen Wettbewerbsvorteil zu
verschaffen, indem er den Entrant mit schlechter Qualität beliefert.
4.
Patent-Pool-Analogy:
Die Terminierungsentgelte erhöhen die Grenzkosten der Netzwerkbetreiber,
wodurch die Endkundenpreise steigen (Preis = Grenzkosten).
Da den Netzwerkbetreibern die Terminierungsentgelte reziprok als Einnahmen
zufließen, können sie durch Festsetzung von gegenseitig hohen
Terminierungsentgelten ihren Gewinn steigern.
Kollusion
Marktanteile und Terminierungsentgelte:
Bei sehr hohen gegenseitigen Terminierungsentgelten (und somit Gewinnen)
kann ein Netzwerkbetreiber seinen Marktanteil drastisch ausbauen, indem er
den Endkundenpreis senkt (Preis < Grenzkosten).
kein Anreiz zu hohe Terminierungsentgelte zu setzen, keine Kollusion
(siehe Laffont/ Tirole (2000), S.187 ff. für weitere Argumente)