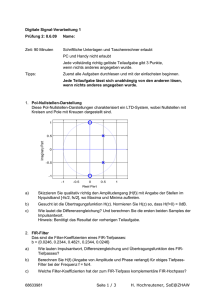
SNT Übung 1

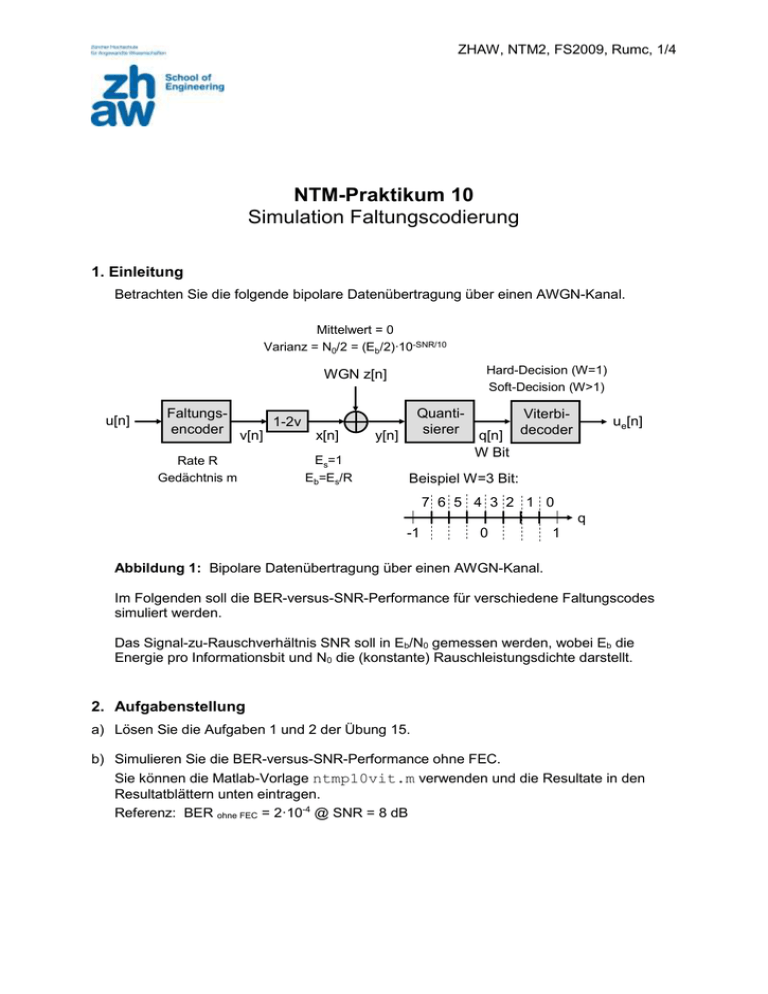
ZHAW, NTM2, FS2009, Rumc, 1/4
NTM-Praktikum 10
Simulation Faltungscodierung
1. Einleitung
Betrachten Sie die folgende bipolare Datenübertragung über einen AWGN-Kanal.
Mittelwert = 0
Varianz = N0/2 = (Eb/2)·10-SNR/10
Hard-Decision (W=1)
Soft-Decision (W>1)
WGN z[n]
u[n]
Faltungs1-2v
encoder v[n]
Rate R
Gedächtnis m
x[n]
Es=1
Eb=Es/R
QuantiViterbisierer q[n] decoder
W Bit
y[n]
ue[n]
Beispiel W=3 Bit:
7 6 5 4 3 2 1 0
q
-1
0
1
Abbildung 1: Bipolare Datenübertragung über einen AWGN-Kanal.
Im Folgenden soll die BER-versus-SNR-Performance für verschiedene Faltungscodes
simuliert werden.
Das Signal-zu-Rauschverhältnis SNR soll in Eb/N0 gemessen werden, wobei Eb die
Energie pro Informationsbit und N0 die (konstante) Rauschleistungsdichte darstellt.
2. Aufgabenstellung
a) Lösen Sie die Aufgaben 1 und 2 der Übung 15.
b) Simulieren Sie die BER-versus-SNR-Performance ohne FEC.
Sie können die Matlab-Vorlage ntmp10vit.m verwenden und die Resultate in den
Resultatblättern unten eintragen.
Referenz: BER ohne FEC = 2·10-4 @ SNR = 8 dB
ZHAW, NTM2, FS2009, Rumc, 2/4
c) Implementieren Sie einen R=1/2, m=2 (constraint-length K=3) Faltungsencoder
mit Hilfe der Matlab-Funktionen trellis=poly2trellis(K,[7,5])und
x=convenc(u,trellis)und verifizieren Sie die Funktionsweise mit dem
Beispiel im Skript.
Implementieren Sie den entsprechenden hard-decision Viterbi-Dekoder mit der
Matlab-Funktion ue=vitdec(yhard,trellis,5*K,'trunc','hard')
und testen Sie die Funktionsweise mit einem einfachen Beispiel.
d) Simulieren Sie die BER-versus-SNR-Performance für einen R=1/2, m=2, OFD
Faltungscode mit hard-decision Dekodierung und vergleichen Sie sie mit der
Performance ohne FEC. Wie gross ist der Codegewinn [dB]?
e) Simulieren Sie die BER-versus-SNR-Performance für einen R=1/2, m=2, OFD Faltungscode mit soft-decision Dekodierung. Wählen Sie dazu die Quantisierungsstufen wie in
Abbildung 1 dargestellt, Matlab-Funktion [dummy,yquan] =
quantiz(y,[-(1-2^(-(W-1))):2^(-(W-1)):1-2^(-(W-1))],...
[(2^W)-1:-1:0]).
Wie gross ist der Codegewinn [dB]?
Wie gross ist der SNR-Gewinn zwischen hard-desision und soft-decision Dekodierung?
Vergleichen Sie den asymptotische Kodierungsgewinn G mit dem theoretischen Wert
G = 10·log10(R·dfree)?
Verifizieren Sie, dass ab einer Traceback-Tiefe von 5(m+1) keine PerformanceVerbesserung mehr resultiert.
Welchen Einfluss hat die W-Bit-Quantisierung auf die Performance?
Überzeugen Sie sich, dass für W=1 Bit hard-decision Dekodierung resultiert.
Zeigen Sie, dass für W=1 Bit die „soft-decision“ und die „hard-decision“ Metrik äquivalent
sind.
Betrachten Sie einige Male das Fehlermuster. Was fällt Ihnen auf?
f)
Simulieren Sie die BER-versus-SNR-Performance für einen R=1/2, m=6, OFD
Faltungscode mit soft-decision Dekodierung.
Wie gross ist der asymptotische Kodierungsgewinn G?
Wie weit weg ist man noch von Shannon’s Limit SNRmin = 0.4 dB?
g) Realisieren Sie eine kleine Demo mit Textdaten.
h) Betrachten Sie das Matlab-Tool bertool.
ZHAW, NTM2, FS2009, Rumc, 3/4
Resultatblatt
ZHAW, NTM2, FS2009, Rumc, 4/4
Resultatblatt