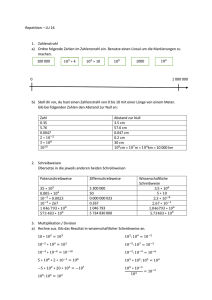
Aufbau des Zahlensystems

Zahlenaufbau_GS1.mcd
GS - 16.05.04 - Zahlen2_Aufbau.mcd
Zurück
Aufbau des Zahlensystems
1. Menge der natürlichen Zahlen: IN = {1 2 3 4 5 ... }
Die natürlichen Zahlen stellen eine geordnete Menge dar.
Daher können wir die Ordnungsrelationen einführen und sagen, dass
die Zahl b größer als die Zahl a ist (b > a), wenn b in der Zahlenreihe hinter a steht, dass
die Zahl b kleiner als die Zahl a ist (b < a), wenn b in der Zahlenreihe vor a steht,
die Zahl a ist gleich der Zahl b (a = b), wenn a und b an gleicher Stelle der Zahlenreihe
stehen.
Als Folge der Ordnung der Zahlen können wir sie auf einer Zahlengeraden (Zahlenstrahl) darstellen.
Darstellung auf dem Zahlenstrahl:
Rechenoperationen:
Für das Rechnen mit (natürlichen) Zahlen werden "Rechenregeln" mit bestimmten Zeichen
festgelegt.
Additon:
Zur Zahl a wird b-mal die Einheit 1 zur Zahl a hinzugefügt.
Für alle a,b ∈ IN gilt: a + b ∈ IN.
Die Addition zweier natürlicher Zahlen führt aus dieser Zahlenmenge nicht heraus.
Multiplikation:
Die Zahl a wird insgesamt b-mal zu sich selber addiert.
Für alle a,b ∈ IN gilt: a ⋅ b ∈ IN.
Die Multiplikation zweier natürlicher Zahlen führt aus dieser Zahlenmenge nicht heraus.
Subtraktion:
Umkehroperation der Addition, falls b < a ist.
Für alle a,b ∈ IN gilt: a − b ∈ IN.
Für beliebige a,b ∈ IN gilt nicht notwendigerweise auch : a − b ∈ IN.
Die Subtraktion zweier natürlicher Zahlen kann deshalb aus dieser Zahlenmenge herausführen.
Division:
Umkehroperation der Multiplikation, falls b "Teiler" von a ist.
Für alle a,b ∈ IN gilt: a:b ∈ IN.
Für beliebige a,b ∈ IN gilt nicht notwendigerweise auch : a:b ∈ IN.
Die Division zweier natürlicher Zahlen kann deshalb aus dieser Zahlenmenge herausführen.
Gertrud Sälzle
1/4
02.03.2006
Zahlenaufbau_GS1.mcd
Beispiele zur Lösung von Gleichungen:
x + 2 = 6 auflösen , x → 4
∈ IN
x + 6 = 2 auflösen , x → −4
∉ IN
x ⋅ 2 = 6 auflösen , x → 3
∈ IN
1
∉ IN
x ⋅ 6 = 2 auflösen , x →
3
1. Erweiterung des Zahlenbereichs . . .
um die "Null" und die Menge der negativen Zahlen: {- 4 - 3 - 2 - 1
0 ... }
Definition der Zahl "Null":
Ergebnis der Subtraktion einer ganzen Zahl von sich selbst.
Für alle a ∈ IN gilt: a − a = 0
2. Menge der ganzen Zahlen: Z = { ... - 3 - 2 - 1 0 1 2 3 ... }
Darstellung auf dem Zahlenstrahl:
2. Erweiterung des Zahlenbereichs . . .
um die endlichen oder periodischen Dezimalbrüche oder gemeinen Brüche.
Die einzelnen Zahlenpunkte liegen jetzt wegen der unendlich periodischen Dezimalbrüche schon
"überall dicht" beieinander, d.h. in beliebig kleinen Intervallen kommen unendlich viele Zahlen vor.
Dazwischen liegen die unendlichen nichtperiodischen Dezimalbrüche (irrationale Zahlen),
sie "durchlöchern" den Zahlenstrahl:
Darstellung auf dem Zahlenstrahl:
Gertrud Sälzle
2/4
02.03.2006
Zahlenaufbau_GS1.mcd
Beispiele zur Lösung von Gleichungen:
x + 2 = 6 auflösen , x → 4
∈ IN
x + 6 = 2 auflösen , x → −4
∈Z
x ⋅ 2 = 6 auflösen , x → 3
∈ IN
1
∈Q
x ⋅ 6 = 2 auflösen , x →
2
x = 4 auflösen , x →
3
2 
 
 −2 
 2 
2 4
 3 
x = auflösen , x →
 −2 
9
 3 
 
 1 
 2 
2
2 
x = 2 auflösen , x →
 1
 2
 −2 
∈Z
∈Q
∉Q
3. Erweiterung des Zahlenbereichs . . .
um die irrationalen Zahlen, z.B.:
Fügt man also zur Menge der rationalen Zahlen die irrationalen Zahlen (unendliche, nichtperiodische
Dezimalbrüche) dazu, so erhält man die Menge der reellen Zahlen.
4. Menge der reellen Zahlen IR
Darstellung auf dem Zahlenstrahl:
Die einzelnen Zahlenpunkte liegen unendlich dicht beieinander, der Zahlenstrahl ist nicht mehr
durchlöchert.
Gertrud Sälzle
3/4
02.03.2006
Zahlenaufbau_GS1.mcd
Beispiele zur Lösung von Gleichungen:
 1
 2
2
2
x = 2 auflösen , x →
 1
 2
 −2






 1
 2
2
 i ⋅2
x = −2 auflösen , x →

1

2
 −i ⋅ 2
∈ IR






∉ IR
Diese Gleichung ist in der Menge der komplexen Zahlen C lösbar.
4. Erweiterung um die imaginären Zahlen in die . . .
Menge der komplexen Zahlen
Gertrud Sälzle
4/4
02.03.2006