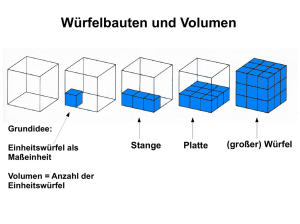
Mathcad - Pyramide.mcd

Extremwertaufgaben
GS - 19.05.06 - Pyramide.mcd
Extremwertaufgabe - Pyramide
- Abschlussaufgabe 2003 - 12 Nichttechnik - Analysis II 3.1
Eine natürliche Zahl heißt vollkommen, wenn sie gleich der Summe ihrer echten Teiler
ist. Beispiel: 6 ist vollkommen, da 6 = 1 + 2 + 3.
Zeigen Sie, dass auch 28 eine vollkommene Zahl ist.
2 BE
3.2.0
Eine Fachoberschule beschließt, ein Denkmal zu errichten. Es soll die Form einer
Pyramide mit quadratischer Grundfläche haben. Sie wird in der Hinsicht vollkommen
sein, dass die Summe aus dem Umfang der Grundfläche und der Pyramidenhöhe
28 dm ergibt.
3.2.1
Bestimmen Sie das Volumen V ( s) der Pyramide in Abhängigkeit von der Länge s einer
Quadratseite und geben Sie eine sinnvolle Definitionsmenge IDV an.
(
3.2.2
3.1
)
4 3
2
[ Teilergebnis: V ( s) = − ⋅ s − 7 ⋅ s ]
3
Berechnen Sie s so, dass das Pyramidenvolumen maximal wird. Geben Sie auch
diesen maximalen Wert Vmax an.
t1 := 1
t2 := 2
t3 := 4
t4 := 7
Summe := t1 + t2 + t3 + t4 + t5 → 28
t5 := 14
q.e.d
Pyramidendenkmal:
2
Grundfläche:
G ( s) := s
Nebenbedingung:
4 ⋅ s + h = 28 auflösen , h → −4 ⋅ s + 28
Volumen:
V ( s) :=
1
3
Höhe: h
⋅ G ( s) ⋅ h ( s) vereinfachen →
(
4 3
2
V ( s) := − ⋅ s − 7 ⋅ s
3
3.2.2
6 BE
Vollkommene Zahlen:
Teiler von 28:
3.2.1
4 BE
h ( s) := −4 ⋅ s + 28
−4
3
2
⋅ s ⋅ ( s − 7)
)
maximale Seitenlänge:
−4 ⋅ s + 28 = 0 auflösen , s → 7
Definitionsmenge:
IDV = {s I 0 < s < 7 }
Maximales Pyramidenvolumen:
Bezeichnung für die Ableitung:
m03_12nta2.mcd
Vs ( s) :=
d
V ( s)
ds
1/2
19.05.2006
Extremwertaufgaben
2
Vs ( s) → −4 ⋅ s +
Ableitung:
Extremum:
Maximum:
⋅s
3
⎛ 0 ⎞ nicht definiert
−4 ⋅ s +
⋅ s = 0 auflösen , s → ⎜ 14
absolutes Maximum, da Scheitel einer
⎜
3
⎝ 3 ⎠ nach unten geöffnen Parabel Maximum ist
2
56
⎛ 14 ⎞ → 5488
81
⎝ 3⎠
Vmax := V ⎜
k := 0
Wähle:
56
Vmax = 67.75
Frame von 0 bis 15
Für Animation k = 0 setzen.
Seitenkante:
s = 3.333
Höhe:
h ( s) = 14.667
vollkommene Zahl: 4 ⋅ s1 + h ( s1 ) = 28
Pyramide
Volumenmaßzahl
80
70
s max
60
50
40
30
20
10
2
m03_12nta2.mcd
2/2
1
0
10
1
2
3
4
5
6
7
8
19.05.2006