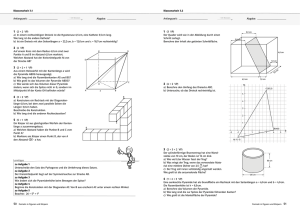
Gegeben seien die Punkte A(2ï-2ï0), B(2ï4ï0), C

Sowa
Analytische Geometrie (Anwendungen_0) Längen, Skalarprodukt, Schnittpunkt von Geraden
Aufgabe: 1 Gegeben seien die Punkte A(2-20), B(240), C(-440), D(-4-20) und S(-116),
die die Eckpunkte einer Pyramide mit der Spitze S bilden. G sei eine Gerade, die durch die Punkte
U(-360) und V(0-36) geht. Alle Längen beziehen sich auf cm.
a) Was wissen Sie über die Grundfläche der Pyramide?
b) Bestimmen Sie den Mittelpunkt der Pyramide! Zur Kontrolle M(-110)
c) Bestimmen Sie den Vektor h für die Höhe der Pyramide!
d) Wie groß ist der Winkel zwischen AC und BD? Zur Kontrolle 90°
e) Weisen Sie nach, dass der Höhenvektor h orthogonal auf den beiden Diagonalenvektoren AC
und BD steht!
f) Bestimmen Sie das Volumen der Pyramide? Zur Kontrolle 72cm³
g) Schneidet die Gerade g die Höhe h ?
h) Falls Aufgabenteil g) verneint werden sollte – geben Sie eine
Gerade g´ an, die durch u geht und h in M schneidet!
i)
Berechnen Sie den Flächeninhalt einer Dreieckseite der Pyramide!
Lösung:
a)
b)
Die Pyramide hat eine quadratische Grundfläche mit der Länge 6 cm.
M(-110), wie oben angegeben.
c)
0
     
h  S  M h  0
6
 
d)
90° Grad. AC und BD stehen orthogonal zueinander.
e)
f)
g)
h)
i)
 0   6

    
h * AC   0  *  6   0
 6  6 
   
666
 72 cm 3
3
  1
1
  3
 3 

 
 
 
 

h : x   1      1 und g : x   6      9  Die Geraden sind windschief.
0
6
 0 
 6 
 
 
 
 
  3
  4
 
 

g ´: x   6      5 
 0 
 0 
 
 
6  18
 12,72 cm 2
2