Aufg vom 25052016 Lösung 233KB May 24 2016 19 - cfg

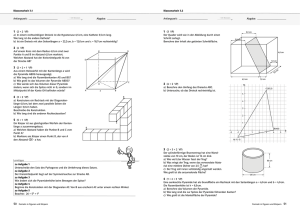
Mathematik 11m2
(Gr)
Aufgabe von Mi 25.05.2016 Analytische Geometrie
LÖSUNG
Auf einen Quader mit der Grundfläche in der x1 - x 2 -Ebene ist eine Pyramide mit folgenden
Eckpunkten aufgesetzt: A(3 | 3 | 7) , B(3 | 3 | 7) , C (3 | 3 | 7) , D(3 | 3 | 7) und S (0 | 0 | 13)
(siehe Abbildung).
a)
Die Ebene E1 verläuft durch die Mitte der
Pyramidenkanten SB bzw. SD und den Punkt C .
Die Pyramidenkante AS liegt auf einer Geraden g .
(1) Berechnen Sie eine Gleichung der Ebene E1
in Parameterform.
E1 :
+r·
=
+s·
(2) Geben Sie eine Gleichung für die Gerade g
an.
g:
b)
=
+t·
(1) Zeigen Sie, dass es sich bei der Pyramide ABCDS um eine quadratische Pyramide
handelt, und berechnen Sie das Volumen der Pyramide ABCDS .
Alle Seiten der Grundfläche sind gleich lang. Dies kann man durch Vektoren berechnen:
| |=
=6;| |=
=6
| |=
=6;| |=
=6
Alle Winkel der Grundfläche betragen 90°. Das ist ersichtlich aus der Lage des Körpers
im Koordinatensystem, kann aber auch nachgewiesen werden mithilfe des
Skalarproduktes. (z.B.
· = 0)
Volumenberechnung:
Vp =
Vq =
· G · h = · 36 · 6 = 72  Das Volumen der Pyramide beträgt 72 VE.
36 · 7 = 252  Das Volumen des Quaders beträgt 252 VE.
Der gesamte Körper hat folglich ein Volumen von 324 VE.
(2) Bestimmen Sie den Flächeninhalt der Mantelfläche der Pyramide.
Die Mantelfläche besteht aus den 4 Dreiecksflächen: ABS, BCS, CDS, DAS
Grundseite  6 LE; Höhe  Länge des Vektors von der Seitenmitte bis zur Spitze S
Diese beträgt
c)
.  MF =
·6·
· 4 ≈ 80,4984 [FE].
Die Dreiecksfläche BCS liegt in einer Ebene E 2 .
F1 (0 | 1 | 11) , F2 (1 | 2 | 9) und F3 (1 | 2 | 9)
(1)
Zeigen Sie, dass das Dreieck F1 F2 F3 gleichschenklig ist.
Ein Dreieck ist gleichschenklig, wenn zwei der drei Seiten gleich lang sind. Wir
bestimmen also die Längen der Seiten F1F2, F2F3 und F3F1.
|
|=
;|
|=
=2
|
|=
 F1F2 und F3F1 sind gleich lang; somit ist das Dreieck
gleichschenklig.
(2)
Zeigen Sie, dass die Punkte F1 (0 | 1 | 11) , F2 (1 | 2 | 9) und F3 (1 | 2 | 9) in der
Ebene E 2 liegen.
E2 :
+r·
=
+s·
LGS aufstellen; dann prüfen, ob es eine Lösung gibt.
(jeweils r und s bestimmen!)
Punktprobe liefert:
d)
E1 :
+
·
+
·
=
 F1 liegt in der Ebene
+
·
+
·
=
 F2 liegt in der Ebene
+
·
+
·
=
 F3 liegt in der Ebene
Prüfen Sie, ob die Gerade g die Ebene E1 schneidet und ermitteln Sie ggf. den Durchstoßpunkt.
=
+r·
+s·
g:
=
+t·
Gleichsetzen:
+t·
+r·
=
=r·
+s·
+s·
-t·
Matrix:
t einsetzen in g:
Lösung mit GTR:
+
·
=
r=
;s=
;t=
Durchstoßpunkt (1|-1|11)