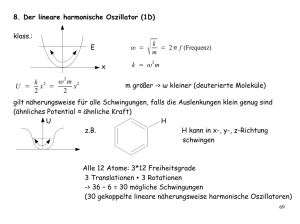
1 6.5 Harmonischer Oszillator in Besetzungszahldarstellung

7Wo_HO-algebraisch
30/31-5-17
6.5
Harmonischer Oszillator in Besetzungszahldarstellung.
Erzeugungs- und Vernichtungsoperatoren.

Wiederholung
klassische Mechanik:
Teilchen oszilliert harmonisch mit x ( t )  A cos (  t  ) , 2 
Energie E 
k
,
m
m 2
m
m2
m
x  U( x )  x 2 
 ...  2 A 2 zwischen 0  E   , kontinuierlich
2
2
2
2
Wellenmechanik (Kapitel 3): Ohne Rechnung ist klar
i
~ ( x, t )   ( x ) e   E t .
 Da Potenzial U(x) zeitunabhängig, folgt für die Wellenfunktionen 
 Da U(x) = U(-x) sind die  ( x ) entweder gerade oder ungerade.
 Da wir die gebundene, eindimensionale Bewegung behandeln, erwarten wir ein diskretes,
nichtentartetes Energiespektrum En.
Mit Rechnung: In Kapitel 3 haben wir  ( x ) und En mit der Sommerfeld´schen Polynommethode aus der stationären Schrödinger-Gleichung

 2 d 2 ( x ) m 2 2

x  (x)  E  (x)
2
2m dx 2
in (wie wir jetzt wissen) Ortsdarstellung bestimmt.
1
x
  2
Vorgehensweise: Nach Variablentransformation y  , b : 

b
 m 
(i)
Asymptote abspalten, Potenzreihenansatz für den "Rest", Rekursionsformel











y2


2
k
1



,
 ( y)  f ( y) e 2
,
a k 2 
ak .
f ( y)   a k y k
(k  1) (k  2)
k 0
1
(ii)
Normierbarkeit sichern
 a1  0 , wenn n ungerade

  2n  1, n  0,1, 2, ... sowie 
 a  0 , wenn n gerade
 0
(iii)
1

E  E n    n 
2

ergibt

 , n  0,1, 2, ...

ein äquidistantes, nichtentartetes Energiespektrum mit den dazugehörigen Eigenzuständen
1
 m  4
n (x)  

  
wobei H n (z) : (1) n e z
2

H n 
2 n n! 
1
m


m 2 
 exp  
x ,

 2


d n  z2
e die hermiteschen Polynome sind. Diese sind Lösungen der
dz n
 d2

d
gewöhnlichen Differentialgleichung  2  2 y  2 n  H n ( y )  0.
dy
 dy

(iv)
für die Aufenthaltswahrscheinlichkeitsdichte fanden wir im Grenzfall n  
lim  n ( x )
n 
2
1

, x A

2
2
A
x



.
 w kl ( x )  

0 , sonst


2

Darstellungsunabhängige, algebraische Lösung des Eigenwertproblems für den
Hamilton-Operator des eindimensionalen harmonischen Oszillators (Dirac)
p 2x m2 2
p̂ 2 m2 2
. Postulat

x 2

 Ĥ  x 
x̂ mit  x̂ , p̂ x   i .
2
2
2m
2m
H(px , x ) 
(6.23)
Dirac definierte eine Operator â und seinen adjungierten â  entsprechend
â :
Def.:
m
i
p̂ x
x̂ 
2
2m 
â  :
m
i
p̂ x
x̂ 
2
2m 
x̂ 



â   â
2m

m  
â  â
p̂ x  i
2


.
(6.24)
Offensichtlich sind weder â noch â  selbstadjungiert. Sie genügen der Vertauschungsrelation
 â, â   1, bzw. â â


 1  â  â
(6.25)
denn
 m

i
m
i
i
i
i
x̂
p̂
x̂ 
p̂ x ,
x̂ 
p̂ x   
, p̂ x  
x̂  
(  i  i )  1 .

x ,

2
2 i 
2  i 
2
2 m 
2m  
 2
Wegen
â  â 
m 2
1
i
1  m2 2 p̂ 2x

x̂ 
p̂ 2x   x̂ p̂ x  p̂ x x̂  
x̂ 
   2
2
2m 
2 
2m
i
 1
 
 2
1
p̂ 2x m2 2


x̂ =    â  â   .
Ĥ 
2m
2
2

folgt
(6.26)
Damit ist das Eigenwertproblem für den Hamilton-Operator Ĥ auf das des Operators N̂  â  â
zurückgeführt.
Wir bezeichnen die Eigenfunktionen des Operators N̂ mit n , die entsprechenden
Eigenwerte mit n und betrachten die Eigenwertgleichung
3
Def.: N̂  â  â , mit N̂ n  n n .
(6.27)
Wir wollen nun zeigen, dass n  0,1, 2, 3, ... ist.
Zur Berechnung der Eigenwerte von N̂ halten wir fest:
(i) Der Operator N̂ ist hermitesch, denn N̂   ( â  â )   â  â    â  â  N̂ .
Also sind die Eigenwerte n reelle Zahlen und die Eigenfunktionen n bilden eine Basis { n }
im Hilbert-Raum .
(ii) Die EW von N̂ sind nicht negativ, denn es gilt n  n N̂ n  n â  â n  â n â n  0 .
Damit ist das Spektrum von N̂ nach unten beschränkt.
(iii) Es gilt N̂ ( â n )  ( n  1) ( â n ) .
Beweis: N̂ â n
( 6.25 )
( 6.27 )
N̂ â n  (â  â ) â n  (â â   1) â n  â (â  â  1) n  â N̂ n  â n  â n n  â n  ( n  1) (â n )
Wenn n Eigenfunktion von N̂ zum Eigenwert n ist, dann ist â n ebenfalls Eigenfunktion
von N̂ , allerdings zum Eigenwert (n-1).
Wegen (6.27) gilt N̂ n  1  (n  1) n  1 . Da die Eigenwerte von N̂ (wie die von Ĥ ) nicht
entartet sind, können sich die Zustände â n und n  1 nur um eine Konstante unterscheiden.
Deshalb muss â n  const n  1 gelten.
Im Gegensatz zu n ist â n noch nicht normiert. Wir finden
â n â n  n â  â n  n N̂ n  n n n  n , und damit schließlich
â n  n n  1
(6.28)
4
(iv) Analog beweisen wir die Gültigkeit der Relationen
N̂ ( â  n )  ( n  1) ( â  n ) , â  n  n  1 n  1 .
(6.29)
( 6.25)
N̂ â  n  â  (â â  ) n  â  (â  â  1) n  â  N̂ n  â  n  â  n n  â  n  ( n  1) ( â  n ) .
Also â  n  const n  1 .
â  n
Normierung:
2
 â  n â  n  n â â  n  n 1  â  â n  (1  n ) n n  1  n .
Also: Ist n Eigenfunktion von N̂ zum Eigenwert n, dann ist â  n
Eigenfunktion von N̂
zum Eigenwert n + 1.
Aus (6.28/29) folgt z.B.
(â  ) 2 n  (n  1)(n  2 n  2
oder
(â )3 n  n (n  1)(n  2) n  3
usw.
(v) Bei wiederholter Anwendung von â auf n könnten im Widerspruch zu (ii) negative
Eigenwerte auftreten. Um das zu verhindern, muss ein Grundzustand, 0 , mit Def.: â 0  0
existieren. Wegen N̂ 0  â  â 0  â  0  0 ist der Eigenwert von N̂ zum Grundzustand 0
gleich Null. Also ist das Spektrum von N̂ nach unten beschränkt.
(vi) Nach oben ist das Spektrum von N̂ dagegen unbeschränkt.
Zum Beweis nehmen wir das Gegenteil an. Sei n max der größte Eigenwert von N̂ , d.h.
â  n max  0 . Dann wäre
0  â  n max
2
 â  n max â  n max  n max â â  n max
( 6.25 / 27 )

n max ( N̂  1) n max  n max  1 ,
also n max im Widerspruch zu (ii) negativ.
Bemerkung: Es existieren keine Eigenfunktionen n von N̂ n  n n mit Eigenwerten n,
die keine natürlichen Zahlen sind. Die Annahme N̂ n  ( n  x ) n , 0  x  1 führt zum
Widerspruch (vgl., z.B., Nolting, Band 3, S. 280).
5
Fazit aus den Eigenschaften (i) – (vi): Die Eigenwerte des Operators N̂ sind n = 0, 1, 2, … .
1

Wegen Ĥ    â  â   (6.26), ergibt sich daraus sofort
2

1

E n    n   , n  0,1, 2 ... ,
2

(6.30)
also das uns aus Kapitel 3 bekannte Energiespektrum des eindimensionalen harmonischen
Oszillators mit seinen diskreten, äquidistanten und nicht entarteten Energieniveaus.
Wir wollen unsere Ergebnisse nun folgendermaßen interpretieren: Der n-te angeregte
Zustand n des harmonischen Oszillators ist mit n Schwingungsquanten der Energie 
besetzt. Wir nennen
(i)
N̂ gemäß N̂ n  n n
den Besetzungszahloperator. Das ist der Operator zur
Observable Anzahl der Schwingungsquanten im Zustand n .
(ii)
â gemäß â n  n n  1
den Vernichtungsoperator. Die Anwendung von â auf
den Zustand n vernichtet ein Schwingungsquant.
(iii)
â  gemäß â  n  n  1 n  1 den Erzeugungsoperator. Die Anwendung von â 
auf den Zustand n erzeugt ein Schwingungsquant.
Naheliegender Weise nennen wir dann die Darstellung zur Basis { n } der Eigenfunktionen
von N̂ die Besetzungszahldarstellung der Quantenmechanik.
Bemerkung: Offensichtlich lassen sich die Operatoren von Observablen, die nach dem
Korrespondenzprinzip Q(p, r )  Q̂  Q(p̂, r̂ ) aus den entsprechenden Phasenraumvariablen
gebildet werden können, durch die Operatoren â  und â ausdrücken (6.24, rechts). Die
Darstellung aller Operatoren von Observablen durch Kombinationen aus Erzeugungs- und
Vernichtungsoperatoren wird als zweite Quantisierung bezeichnet. Sie ist von grundlegender
Bedeutung für die quantenmechanische Beschreibung von Vielteilchensystemen und wird
ausführlich im Kurs ThPh V, QM II behandelt.
6

Eigenfunktionen von Ĥ
Ĥ und N̂ haben gemeinsame Eigenfunktionen. Sie lassen sich durch aufeinanderfolgende
Anwendung von â  aus dem Grundzustand 0 gewinnen:
1
1 
1 
â 1 
(â  ) 2 0
â 0 , â  1  2 2 , â  1  2 
1 2
2
1
â  0  1 1 , â  1  1 
also
n 
1
(â  ) n 0 , n  0,1, 2, ...
n!
(6.31)
In Ortsdarstellung erhalten wir die Ergebnisse aus Kapitel 3.
Grundzustand: Wir projezieren â 0 auf x
m
i
x̂ 
p̂ x 0 
2
2 m 
0  x â 0  x

und finden mit (6.24) die Differentialgleichung
m
i
x x̂ 0 
2 
2 m 
x x 0  x 0 ( x )
x p̂ x 0



i

d ( x )
d
x 0   i 0
dx
dx
 d 0 ( x )
m
x 0 (x ) 
0.
2
2 m dx
Über Trennung der Variablen,
m 2m
d 0
m

x dx 
x dx und Normierung folgt
0

2 
1
m
 m  4  2  x 2
0 (x )  
.
 e
  
(6.32)
Einschub: Angeregte Zustände ( Übungsblatt)
Sukzessive erzeugen wir aus  0 ( x ) die Wellenfunktionen der angeregten Zustände, z.B.

1 ( x )  x 1  x â 0  

denn mit
m
 d 
 x0 
x
2
2m dx 
d 0
m

d

x  0 (s.o.) ist 
x 0 
dx

2 m dx
2m
x 0 (x)

m
x 0
2
7
d
m
x mit


dx
Bemerkung: Die Substitution q :
m d
d
vereinfacht die
in p̂ x   i
 dq
dx
Ausdrücke erheblich, denn nun ist
â 
1 
d 
1 
d 
 q   , â  
 q  
dq 
dq 
2
2
also
1
 n (q) : q n 
q (â  ) n 0 
n!
n

d 
 q    0 (q ) .
dq 
2 n n! 
1
(6.33)
Zeigen Sie, dass daraus
1
 m  4
 n (q )  

  
1
2n n!
H n (q ) e
folgt, wobei H n (q )  (1) n e q
2

q2
2
, n  0,1, 2, ...
d n  q2
e die Hermite´schen Polynome vom Grad n sind.
dq n
Überzeugen Sie sich, dass H n (q ) die Lösungen der linearen homogenen gewöhnlichen
Differentialgleichung 2. Ordnung

 d2
d
 2  2q  2n  H n (q )  0 sind.
dq

 dq
Fazit: Damit ist der Anschluss an die Ergebnisse vollzogen, die wir in Kapitel 3 bei der
Behandlung des eindimensionalen harmonischen Oszillators nach der Sommerfeld´schen
Polynommethode erzielt haben. Hier haben wir Energiespektrum und Eigenfunktionen
ausschließlich unter Verwendung der Vertauschungsrelation zwischen Orts- und
Impulsoperator x̂ , p̂ x   i bestimmt.
Die verwendete Besetzungszahldarstellung mit den eingeführten Erzeugungs- und
Vernichtungsoperatoren ist Grundlage der sogenannten II. Quantisierung, die im Kurs
Quantenmechanik II (Masterstudium) ausführlich behandelt wird.
8
Einschub: Glauber-Zustände
1963 zeigte R. J. Glauber (geb. 1925, Nobel-Preis für die Entwicklung der Theorie der
kohärenten Zustände in der Quantenoptik; R. J. Glauber, Coherent and Incoherent States of
the Radiation Field, Phys. Rev. 131, 2766 (1963)), dass die elektromagnetische Welle einer
Lasermode am besten durch  kohärente Zustände  gemäß
â     ,   C komplex
beschrieben werden kann. Diese kommen klassischen elektromagnetischen Wellen sehr nahe,
weil der Erwartungswert der elektrischen Feldstärke im Zustand  unabhängig vom
Erwartungswert der Teilchenzahl die Form einer klassischen elektromagnetischn Welle hat.
Ursprünglich entdeckte Erwin Schrödinger die kohärenten Zustände, als er nach einem
Zustand des quantenmechanischen harmonischen Oszillators suchte, der weitestgehend dem
klassischen harmonischen Oszillator entspricht. Vgl. E. Schrödinger, Der stetige Übergang
von der Mikro- zur Makromechanik, Die Naturwissenschaften 14, 664-666 (1926). Er zeigte,
dass der kohärente Zustand im Fall des harmonischen Oszillators ein Gauß´sches Wellenpaket
ist, dass im parabolischen Potenzial U ( x )  k / 2 x 2 hin und herläuft, ohne dabei seine Ortsund Impulsunschärfe zu verändern (vgl. Animation in Wikipedia unter dem Stichwort 
kohärenter Zustand.)
Die sogenannten kohärenten oder Glauber-Zustände  haben interessante Eigenschaften,
die die Bezeichnung quasi-klassische Zustände rechtfertigen (Beweise Übungsblatt):
(i)
x

p x
!



 "minimale Wellenpakete"
2
(ii) Für große Werte  sind die Unschärfen von x̂ , p̂ x und Ĥ sehr klein.
(iii) x

und p x

genügen den klassischen Bewegungsgleichungen (oszillieren mit
Frequenz  ), wohingegen x
n
 px
n
0.
9
Vorgehensweise zum Beweis von (i) – (iii) (u.U. als Übungsaufgabe):
1) Zeige, das
 e


2
2


n 0
n
n
n!
ein normierter Eigenzustand  des Vernichtungs-
operators â zum Eigenwert  ist.
2) Eigenzustände 
zu verschiedenen Eigenwerten  sind nicht orthogonal ( â ist
nichtnormal, da [ â , â ]  0 ).
3)

2
e
  
2
.
Fazit: Kohärente Zustände schlagen die Brücke zur klassischen Physik harmonischer
Oszillatoren. Besonders wichtig sind sie in der Quantenoptik.
■
Ein Fadenpendel mit m  1 kg und   10 cm hat   1015 .
10