N - TU Freiberg
Werbung
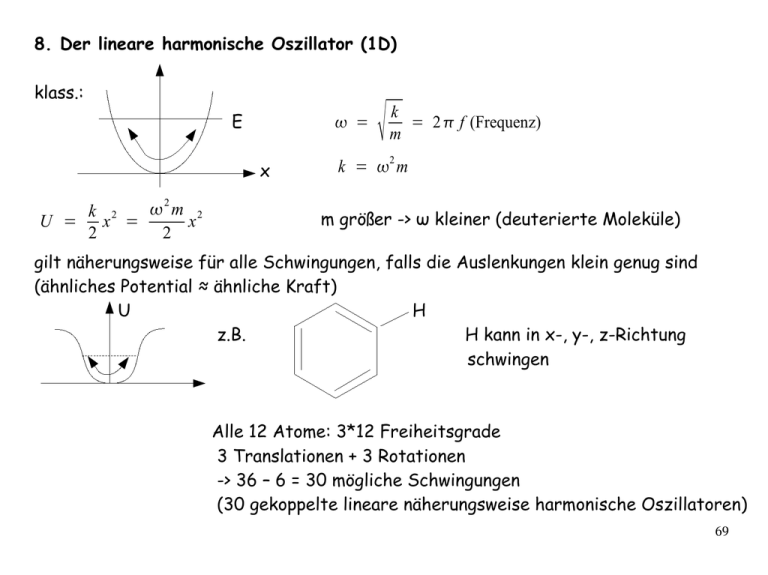
8. Der lineare harmonische Oszillator (1D) klass.: E = x 2 m 2 k 2 U = x = x 2 2 k = 2 f (Frequenz) m k = 2 m m größer -> ω kleiner (deuterierte Moleküle) gilt näherungsweise für alle Schwingungen, falls die Auslenkungen klein genug sind (ähnliches Potential ≈ ähnliche Kraft) U H z.B. H kann in x-, y-, z-Richtung schwingen Alle 12 Atome: 3*12 Freiheitsgrade 3 Translationen + 3 Rotationen -> 36 – 6 = 30 mögliche Schwingungen (30 gekoppelte lineare näherungsweise harmonische Oszillatoren) 69 Quantenmechanik: Wir suchen stationäre Zustände (also mögliche Energien) der stationären Schrödingergl., H n x = E n n ist zu lösen ℏ2 d 2 m 2 2 H n = − x n = E n n 2m dx 2 n 2 m/ℏ x eingeführt: = 0 = a 0 e n x = n −2 2 −2 2 1 = a1 e ⋅ ⋅ ⋅ −2 2 n n = e [a 0 a 1 a 2 ...a n ] 2 a j2 d n −y H n = −1 e ne dy 2 j−n = a j1 j2 j n x ~ e −m 2 x 2ℏ Hermitesche Polynome Hn(y) n H n x⋅ m ℏ y 1 Energieeigenwerte E n = n ℏ 2 2 2 70 Statt Lösung der zeitunabhängigen Schrödingergleichung wählen wir eine geschickte Lösungsmethode, bei der nur algebraische Gleichungen gelöst werden müssen. Wir definieren zwei neue Operatoren A und A+, um den Hamiltonoperator auf eine möglichst einfache mathematische Form zu bringen. Aus Gründen, die (hoffentlich) später klar werden: A = m x 2ℏ A*= A = ip x Vernichtungsoperator 2 ℏ m m x − 2ℏ ip x Erzeugungsoperator 2 ℏ m A ist keine Messgröße, da A ≠ A+ (nicht selbstadjungiert) wir kennen [x, px] = i ħ , [x, x] = [px, px] = 0 + [ ] [ ] [ ][ ] ip −i p x ip m m m −i p x m x, x x , x, x , x 2ℏ 2ℏ 2 ℏ 2 ℏ 2 ℏ m 2 ℏ m 2 ℏ m 2 ℏ m −i i −i −i = [ x , p x ] [ p x , x]= [ x , p x ]= i ℏ=1 2ℏ 2ℏ ℏ ℏ [A, A ] = 71 Wir drücken jetzt den Hamiltonoperator mit Hilfe der Operatoren A und A+ aus. 2 2 px m 2 H = x 2m 2 2ℏ 1 x= A A + m 2 −i p x = 2 ℏ m A− A + 2 ℏ x 2= A 2 AA + A + A A + 2 2m 1 p 2x =−ℏ m A 2 − AA +− A + A A + 2 2 A = A = Einsetzen in den Hamiltonoperator ergibt zusammen mit m x 2ℏ m x − 2ℏ + ip x 2 ℏ m ip x 2 ℏ m + + [ A , A ]= A A − A A=1 ℏ 2 ℏ 2 ℏ A − AA+ − A + A A+ 2 A AA + A + A A + 2= 2 AA+ A+ A 4 4 4 ℏ 1 = 2 A + A1=ℏ A+ A 2 2 H = − 72 Durch die Umformungen haben wir das Problem der Lösung der zeitunabhängigen Schrödingergleichung für den harmonischen Oszillator auf die Lösung eines Eigenwertproblemes für einen neuen Operator zurück geführt. + N =A A N ist hermitesch Besetzungszahloperator N+ = (A+A)+ = A+ (A+)+ = A+A = N -> reelle Eigenwerte N ∣n ⟩ = n∣n ⟩ ∣n ⟩ = n sei ein normierter Eigenzustand = A +∣n ⟩ AA+ − A+ A = 1 N = A + A A +∣n ⟩= A + 1 A + A ∣n ⟩= A + 1 N ∣n ⟩=n1 A+∣n ⟩= n1 also ist A+|n> = ζ ein Eigenzustand von N mit Eigenwert (n+1) _ = A ∣n ⟩ N _= A + A A∣n ⟩= AA + −1 A∣n ⟩= AA + A− A ∣n ⟩= AN − A∣n ⟩= = A N −1∣n ⟩=n−1 A ∣n ⟩= n−1 _ 73 Genauso lässt sich zeigen, dass A∣n ⟩ ein Eigenzustand von N mit Eigenwert n-1 ist. Mit A+ klettert man von n um 1 zum Eigenwert n+1, mit A steigt man um 1 hinab. Hochklettern ist kein Problem, wohl aber das Absteigen, da + ⟨n∣N∣n⟩ = ⟨n∣A A∣n⟩ = ⟨ A n∣ A n⟩ n , N n = n , A + A n = A n , A n ≥ 0 kein Eigenwert von N darf negativ werden! Der Ausweg: Es gibt einen Zustand ∣0 ⟩ = 0 , der von Aφ0 = 0 vernichtet wird. φ0muss von Null verschieden sein (||φ0|| = 1). Im Zustand φ0 hat N den kleinstmöglichsten Eigenwert n = 0. 1 1 + H =ℏ A A =ℏ N 2 2 Die Schwingung des harmonischen Oszillators im Zustand |n> besteht aus n Schwingungsquanten (Vibronen), die alle die Energie ћω besitzen. Der Hamiltonoperator H beschreibt damit ein System solcher Schwingungsquanten gleicher Energie (ћω), bei dem sich n ändern kann. Der Operator N fragt die Anzahl der Vibronen im Zustand |n> ab (Besetzung). Die Anwendung von A+ (A) auf den Zustand |n> erzeugt (vernichtet) ein Schwingungsquant. 74 Die Grundzustandswellenfunktion φ0(x) (Wellenfunktion des Vakuumzustandes |0> ) A 0 x = A ∣0 ⟩ = 0 m ℏ d x x = 0 2ℏ 2m dx 0 0 x = c 0 e −m 2 x 2ℏ −m d 0 x = c 0 x dx ℏ ℏ m = 2m ℏ e −m 2 x 2ℏ 1 = ∫ dx * 0 2 x 0 x = c 0 −∞ q = = ∣c0∣ 0 ∞ ∫ dx e −m 2 x ℏ −∞ m x ℏ 2 −m x ℏ m 2ℏ Normierung ∞ = ℏ m dq = ∞ m dx ℏ ∫ dq e−q −∞ 2 c0 = 4 m ℏ 75 Die übrigen Eigenfunktionen durch wiederholtes Anwenden von A+ 1 = ⋅ ⋅ ⋅ m 1 d − 0 = d ℏ 2 1 4 1 d − d 2 e − 2 2 n 1 d n = − 0 n d n ! 2 Hermitesche Polynome Hn = e n = x2 2 n d x− e dx 1 n ! 2 n m ℏ − 1 4 x2 2 e d n −x = −1 e e dx n n −2 2 H n x2 2 n = 0, 1, 2, . . . 76 Damit kennen wir die Eigenwerte, die Eigenvektoren von N = A+A können wir konstruieren durch 1 = A + 0 ⋅ ⋅ ⋅ 1 n = A+ n 0 n ! n1 ∣n1 ⟩ A∣n ⟩ = n ∣n−1 ⟩ diskret, nicht entartet mit äquidistantem Abstand ћω (da wir von n = 0 starten und 1 E n = ℏ n 2 E0 = A +∣n ⟩ = immer +1 dazugeben n = positive ganze Zahl) 1 ℏ 2 Nullpunktsenergie 1 E0 = ℏ 2 unmöglich x px = ℏ 2 77 Die berechneten Eigenfunktionen φn haben genau n Nullstellen. IR-Absorption zwischen Zuständen verschiedener Parität (Dipolauswahlregeln) ~ ⟨n∣x∣m ⟩ = ∫ *n x m dx Integral mit symmetrischen Grenzen von einer ungeraden Funktion ergibt Null. n=0 -> n=1 starker Übergang n=0 -> n=2 verboten (gleiche Parität) n=0 -> n=3 möglich, aber schwächer als Übergang nach n=1 78 Bedeutung des harmonischen Oszillators für die Physik Jedes schwingungsfähige System (Moleküle, Festkörper) ist näherungsweise ein System gekoppelter harmonischer Oszillatoren. Durch Transformation in „Normalkoordinaten“ kann man immer ein System ungekoppelter harmonischer Oszillatoren erhalten. Nullpunktsenergien sind immer vorhanden und können die Stabilität beeinflussen (Verringerung der Bindungsenergie), sie tragen zur Gesamtenergie und damit auch zur Bindungsentalphie bei. technische Nutzung z.B. in Isotopenfraktionierung 13 C reichert sich in anorganischen Verbindungen weniger an, als in Verbindungen biogenen Ursprunges. Bestätigung der Planckschen Erklärung der Hohlraumstrahlung. Die Quantisierung von Feldern in der Quantenelektrodynamik beruht auf Erzeugungsund Vernichtungsoperatoren, und damit auf den Eigenschaften des harmonischen Oszillators. 79











