Systemwissenschaften, Mathematik und Statistik

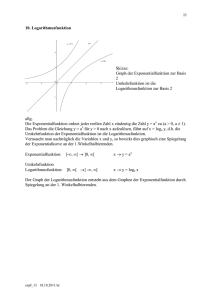
Systemwissenschaften,
Mathematik und Statistik
Systemwissenschaften:
1 WS: Systemwissenschaften 1, VO 2std
2 SS: Systemwissenschaften 2, VO 2std
Übung zu Systemwissenschaften, UE 2std
3 WS: Systemwissenschaften 3, VU 2std
4 SS: Angewandte Systemwissenschaften, VO 2std
Inhalte:
Systemwissenschaftliche Basiskonzepte
Systemanalyse
Wirkungsdiagramme, Feed-back loops
Grundkonzepte der Modellierung
Stakeholderanalyse
Stoffflussanalyse
Mathematische Beschreibung von Systemen
Numerische Simulation (Vensim)
Datenerhebung, Datenunsicherheiten
Grenzen der Modellierung
Anwendung in Fachschwerpunkt
Mathematik und Statistik:
1 WS: Integral- und Differentialrechnung für USW, VU, 4std
2 SS: Vektorrechnung für USW, VU, 3std.
3 WS: Statistik für USW, VO, 2std
3 WS: Proseminar zu Statistik für USW, PS, 1 std
Inhalte (Mathematik):
Reelle Zahlen und Ungleichungen, komplexe Zahlen
Elementare Funktionen und ihre Umkehrfunktionen
Grenzwert und Stetigkeit, Folgen
Differentialrechnung (in mehreren Veränderlichen)
Integralrechnung in einer Veränderlichen
Lineare Gleichungssysteme und Vektoren
Lineare Abbildungen und Matrizen
Koordinatentransformationen
inneres Produkt
Determinanten, Eigenwerte und Anwendungen
Inhalte (Statistik):
Ein- und zweidimensionale Daten, Kennzahlen
graphische Darstellung
Wahrscheinlichkeitsrechnung,
Zufallsgrößen und Verteilungen
Schätzfunktionen
statistische Tests (Ein- und Zweistichprobenprobleme)
Chi-quadrat Test
SW1:
Einfuehrung, Geschichte, Konzepte
Wirkungsdiagramm
Regression, empirische Modelle
statische und dynamische Mengenbilanzen (mM)
SW2:
System Dynamics (Vensim)
Szenarien
Modelle mit Differentialgleichungen
Daten, Wahrscheinlichkeit, Sensitivitaet
Vermittlung eines Eindrucks von
●
●
●
Integral- und Differentialrechnung fuer USW
SW2: Kinetik chemischer Reaktionen
Mathematisches Modell
Anpassung an Daten
Bakk- oder Masterarbeit: konkretes Beispiel
2. EXPONENTIALFUNKTION, LOGARITHMUSFUNKTION
47
Beispiel 2.1. Die Biomasse einer Bakterienkultur verdoppele sich alle 3 Stunden. Anfänglich
sind 3 g vorhanden. Wie entwickelt sich die Biomasse im Laufe der Zeit? (Zeiteinheit Stunden)
Lösung. Es bezeichne B(t) die Biomasse zur Zeit t (in Stunden). Zu Beginn des Experimentes
(t = 0) war B(0) = B0 g Biomasse vorhanden. Da sich die Biomasse alle 3 Stunden verdoppelt, gilt
B(t + 3) = 2B(t).
Unter der Annahme einer bestandsproportionalen Zuwachsrate folgt mit ∆t = 1
B(t + 1) − B(t) = λB(t),
also
B(t + 1) = rB(t)
mit r = λ + 1. Für die unbekannte Konstante r ergibt sich aus
!
B(t + 3) = rB(t + 2) = r2 B(t + 1) = r3 B(t) = 2B(t)
die Beziehung
r3 = 2,
√
3
d.h. r =
2.
Es folgt
B(1) = rB0 ,
B(2) = rB(1) = r2 B0 ,
B(3) = rB(2) = r3 B0 , etc.
Man erkennt das Bildungsgesetz für die Dynamik der Biomasse
t
B(t) = B0 rt = B0 2 3 .
¤
Beispiel 2.2. Wir betrachten nun die Entwicklung einer Bakterienkultur unter der Annahme
P (t + ∆t) − P (t) ≈ λP (t)∆t.
(vgl Beispiel 0.4). Dieser Ansatz ist nur für kurze Zeitintervalle ∆t sinnvoll, da sich während dieser
Zeitspanne die Populationsgröße ändert. Für hinreichend kurze Zeitintervalle kann man allerdings
davon ausgehen, daß nur die zur Zeit t vorhandenen Bakterien sich vermehren können. Die Populationsgröße zur Zeit t = 0 sei P (0) = P0 , gesucht ist P (t) für t > 0.
Lösung. Um P (t) zu berechnen, unterteilt man das Intervall [0, t] in n gleich lange Teilintervalle
der Länge ∆t = nt und setzt ti = ni t, i = 0, . . . , n. Es folgt
P (tn ) ≈ P (tn−1 ) + λ∆tP (tn−1 )
t
= (1 + λ )P (tn−1 )
n
t
≈ (1 + λ )(P (tn−2 ) + λ∆tP (tn−2 ))
n
t
= (1 + λ )2 P (tn−2 ) = · · ·
n
t
≈ (1 + λ )n P (t0 ).
n
Es liegt nahe zu vermuten, daß eine Verfeinerung der Unterteilung des Zeitintervalles [0, t] zu einer
besseren Approximation von P (t) führt und im Idealfall
t
P (t) = lim (1 + λ )n P0
n→∞
n
48
4. ELEMENTARE FUNKTIONEN
gilt. Dieser Grenzwert existiert, denn man kann (mit einigem Aufwand) zeigen
x
lim (1 + )n = ex , x ∈ R,
n→∞
n
wobei e = 2, 71828... die Euler’sche Zahl bezeichnet. Man erhält somit für die Populationsgröße
P (t) = P0 eλt .
¤
Die beiden Beispiele führten uns zwanglos auf einen neuen Typ von Funktionen, bei dem die
unabhängige Variable im Exponenten steht:
Definition 2.1 (Exponentialfunktion). Die Exponentialfunktion ist definiert durch
(
R→R
exp =
x 7→ limn→∞ (1 + nx )n .
Anstelle exp(x) schreibt man auch ex .
Man kann zeigen, daß exp(x) tatsächlich mit der reellen Potenz ex übereinstimmt. Dies wurde in
der Bezeichnung bereits vorweggenommen. Es gelten somit die Rechenregeln aus Satz 1.4. Manchmal
ist es zweckmäßig nicht nur die Eulersche Zahl als Basis für die Exponentialfunktion zur Verfügung
zu haben:
Satz 2.1 (Satz und Definition). Die Exponentialfunktion zur Basis a > 0, a 6= 1
(
R→R
expa :=
x 7→ ax
hat folgende Eigenschaften:
(1) expa ist stetig.
(2) expa ist eine Bijektion von R auf (0, ∞).
(3) expa ist streng monoton wachsend für a > 1 und streng monoton fallend für a < 1.
(4) Für alle x ∈ R gilt expa (x) > 0, expa (0) = 1.
(5) limx→∞ expa (x) = ∞ und limx→−∞ expa (x) = 0 für a > 1
Abbildung 4.7 illustriert das qualitative Verhalten von expa für a = 2 und a = 12 .
Satz 2.2.
(1) Für positive λ wächst die Exponentialfunktion eλt rascher als jede Potenzfunktion, insbesonders gilt
ta
lim λt = 0,
für alle a > 0
t→∞ e
(2) Für negative λ konvergiert die Exponentialfunktion eλt rascher gegen Null als jede Potenzfunktion anwächst, insbesonders gilt
lim ta eλt = 0,
t→∞
für alle a > 0
Da jede Exponentialfunktion R bijektiv auf (0, ∞) abbildet, existiert die Umkehrfunktion:
Definition 2.2 (Logarithmusfunktion).
(1) Die Umkehrfunktion der Exponentialfunktion expa : R → (0, ∞), a > 0, a 6= 1 definiert die Logarithmusfunktion zur Basis a
loga : (0, ∞) → R
(2) Somit gilt: x = loga (y) ⇔ y = expa (x) = ax
(3) loga (y) heißt Logarithmus von y zur Basis a.
Donorsubstanz
Kommentar
gesucht
gesucht
bekannt
bekannt
bekannt
bekannt
dynamische Mengenbilanzen
d
cD (t) = −k1 cD (t),
dt
d
cN O (t) = k1 cD (t) − k2 o2 cN O (t)2 .
dt
Anfangsbedingungen
cD (0) = c0 ,
cN O (0) = 0.
Abbildung 3.3: Simulation des NO-Experiments
x10 -5
1*
k1=3.0000e-003, k2=8.0000e+006
0.9
0.8
*
0.7
Donor: --,*; NO: -,o
Größe
t
cD (t)
cN O (t)
c0
o2
k1
k2
Tabelle 3.2: Stickoxidbildung durch Zerfall einer
Modellgrößen
Einheit
Benennung
s
Zeit
mol/l
Konzentration Donor
mol/l
Konzentration NO
−6
5.6 · 10 mol/l Anfangskonzentration Donor
2 · 10−4 mol/l
Konzentration O2
−3
3 · 10 1/s
Reaktionskonstante Donorzerfall
6 2
2
8 · 10 l /(mol s) Reaktionskonstante NO-Abbau
0.6
*
0.5
0.4
*
0.3
o
o
o
*
o
0.2
o
*
o
o
o
*
0.1
0o
0
o
*
*
200
400
600
*
800
t
Simulation: Donor strichliert, NO durchgezogen.
gegebene Daten: Donor Sternchen, NO Kreise.
30
o
o
*
*
1000
o
*
1200