Document

165
19 Redoxgleichgewichte (Elektronenübertragungsreaktionen)
Vergleich „Protochemische“ und „Elektrochemische“ Spannungsreihe
„Protochemische“ Spannungsreihe
Korrespondierende Säure-Base-Paare
Säure
korrespondierende Base + H+
pKS
HCl
Cl-
+ H+
-7
+ H+
0
+ H+
4,75
+ H+
9,25
Protonenübertragung
Säurestärke
H3O+
H2O
CH3COOH
CH3COO-
NH4+
NH3
Basenstärke
Eine starke Säure steht in Verbindung (korrespondiert) mit einer schwachen Base.
S1 + B2
B1 + S2
„Elektrochemische Spannungsreihe“
Korrespondierende Redoxpaare
Reduzierte Form
korrespondierende oxidierte Form + ne-
Unedles Metall
Metallkation
E° [V]
+ ne-
<0
+ 2e-
0
+ ne-
>0
Elektronenübertragung
Reduktionskraft
H2 + 2H2O
2H3O+
Edles Metall
Metallkation
Oxidationskraft
Ein starkes Reduktionsmittel korrespondiert mit einem schwachen Oxidationsmittel.
Red1 + Ox2
Ox1 + Red2
166
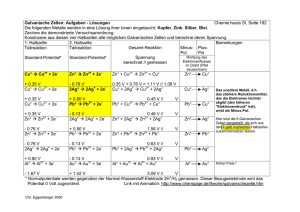
Versuche: Metall + Metallkation
a)
0
+I
Cu(s) + 2Ag+
0
2Ag(s)
+II
+ Cu2+
b)
0
+II
Zn(s) + Cu2+
0
Cu(s)
c)
Cu(s) + Zn2+
keine Reaktion
+II
+ Zn2+
Zn
Zn2+
+ 2e-
Reduktions- Cu
kraft
Ag
Cu2+
Oxidations+ 2ekraft
Ag+
+ e-
Versuche: Halogenid + Halogen
a)
-I
2I-
+
0
Cl2
b)
-I
2Br- +
0
Cl2
0
Br2 +
-I
2Cl-
c)
-I
2I-
0
Br2
0
I2
-I
2Br-
+
2IReduktions- 2Brkraft
2Cl-
0
I2
+
-I
2Cl-
I2
+
+ 2e-
OxidationsBr2 kraft
+ 2eCl2
+ 2e-
167
19.1
Die Spannungsreihe
Die Reaktion von Cu(s) mit Ag+(aq)-Ionen soll im folgenden näher betrachtet werden.
Steckt man ein Cu-Blech in Wasser, so können an der Oberfläche einige Ionen das Metall verlassen.
Die Elektronen bleiben an der Oberfläche zurück und verhindern durch die elektrische Anziehung,
dass sich die Metallionen aus der Nachbarschaft der Oberfläche entfernen, so dass eine
„elektrochemische Doppelschicht“ aus Cu2+(aq)-Ionen und Elektronen entsteht (s.u.). Jedes Metall
besitzt einen charakteristischen „Lösungsdruck“, der wiederum einen entsprechenden
Elektronenüberschuss im Metall erzeugt. So ist der Lösungsdruck von Kupfer größer als der von
Silber (Kupfer ist unedler als Silber). Beim obigen Versuch (unten schematische Darstellung)
diffundieren die Ag+-Ionen zur elektrochemischen Doppelschicht an der Phasengrenzfläche Cu(s)
/Elektrolyt und nehmen vom Cu-Metall Elektronen unter Bildung des edleren Silbers auf.
Cu(s) + 2Ag+(aq)
Cu-Blech
Cu2+
2Ag
eCu2+ -Cu
Ag ee
Cu2+ e
Ag -Cu
2+ e
Cu
ee-Cu
Cu2+ e+
Cu2+(aq) + 2Ag(s)
1.
Halbreaktion (Oxidation)
Cu(s)
H2O
Cu2+ + 2e-
Cu
2.
Cu
Halbreaktion (Reduktion)
2Ag+ + 2e-
Cu
2Ag(s)
Halbreaktionen örtlich trennen und
2NO3-
elektrisch leitend verbinden
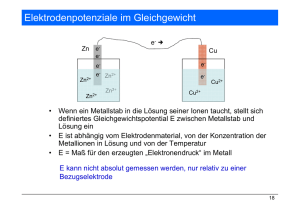
Elektrochemische Doppelschicht an der Phasengrenze Cu(s) und Elektrolytlösung
aus Cu2+(aq)-Ionen und negativ geladener (e = Elektronen) Cu-Oberfläche
Um ein quantitatives Maß für den unterschiedlichen edlen Charakter von Cu und Ag zu erhalten,
werden die beiden Halbreaktionen (Oxidation und Reduktion, s.u.) der betrachteten Redoxreaktion
örtlich voneinander in Halbzellen getrennt. In der einen Halbzelle taucht ein Ag-Stab in eine wässerige
Lösung von AgNO3(aq) (c = 1 mol/l) und in der anderen Halbzelle ein Cu-Stab in eine Lösung von
CuSO4(aq) (c = 1 mol/l). Verbindet man nun das Cu-Blech durch einen Draht mit dem Ag-Blech, so
werden die Elektronen vom Ort höheren „Elektronendrucks“ (Kupfer) zum Orte niedrigeren
„Elektronendrucks“ verschoben. Aus dem unedleren Cu-Blech gehen Cu2+-Ionen in Lösung über und
am Ag-Blech tritt die umgekehrte Reaktion (Ag+
Ag) ein.
168
Elektronenstrom(-verschiebung)
_
_
Elektronenabführende
Anode
Leiter-Draht
_
Elektronenzuführende
Kathode
Salzbrücke
Ag
Cu
_
Cu2+ _
_
Cu2+ _
_
Cu2+ _
_
Cu2+ _
Cu2+
Ag+
_
Ag+ _
H2O
H2O
_
2 Ag
_
SO42- 2Ag+
Cu2+
Cu-Halbzelle
(Cu-Elektrode)
2NO3-
Ag-Halbzelle
(Ag-Elektrode)
Lösungsdruck
Cu
Elektronendruck im Cu
>
>
Ag
Ag
Elektronen fließen vom Cu zum Ag:
Cu
Cu2+ + 2e-
Oxidation
unedleres Metall
löst sich auf
2Ag+ + 2eReduktion
edleres Metall
scheidet sich ab
Zellreaktion:
Cu + 2Ag+
Cu2+ + 2Ag
2Ag
169
Der elektrische Strom, der zwischen der Cu- und der Ag-Halbzelle in der obigen Zelle fließt, kann für
die Verrichtung von elektrischer Arbeit genutzt werden. Derartige Zellen, in denen chemische Energie
in elektrische Energie umgewandelt wird, nennt man Galvanische Elemente. Ein schon sehr früh
genutztes Galvanisches Element ist das Daniell-Element:
Entladereaktion einer galvanischen
Zelle (Daniell Element)
<
In den obigen Zellen fließt ein Strom von der Anode zur Kathode (vom Ort größeren
Elektronendrucks zum Ort kleinen Elektronendrucks = vom höheren Potential zum niederen
Potential). Dieser Strom kann nur fließen, weil die Elektrodenpotentiale unterschiedlich sind. Das
einzelne Elektrodenpotential lässt sich nicht messen, aber die Differenz zwischen den
Elektrodenpotentialen (das Potentialgefälle = Zellspannung). Mit Hilfe eines Voltmeters erhält man
folgende Zellspannungen (= EMK, Elektromotorische Kraft):
Galvanische Zelle
Zellspannung [V]
Cu(s)/Cu2+(aq)//Ag+(aq)/Ag(s)
0,46
Zn(s)/Zn2+(aq)//Cu2+(aq)/Cu(s)
1,1
Zn(s)/Zn2+(aq)//Ag+(aq)/Ag(s)
1,56
(/)
(//)
senkrechter Strich für Phasengrenzfläche zwischen Metall und Elektrolyt
zwei senkrechte Striche für Trennung von Anoden- und Kathodenraum (stehen für
Diaphragma oder Salzbrücke)
Die Unterschiede zwischen den Elektrodenpotentialen sind im folgenden Schema zusammengefasst.
Die Zn/Zn2+-Elektrode besitzt das höchste Potential:
170
Zn/Zn2+
Potential
1,1 V
1,56 V
Cu/Cu2+
0,46 V
Ag/Ag+
Den Aufbau einer Wasserstoffelektrode (H2/2H3O+) zeigt folgende Abbildung:
Die Standard-Wasserstoffelektrode
Eine platinierte - mit fein verteiltem Platin überzogenes - Platin-Blech taucht in eine Lösung, die
H3O+-Ionen enthält, und wird von H2-Gas umspült. H2 löst sich im fein verteilten Platin atomar.
An der Phasengrenzfläche Platin/Elektrolyt stellt sich das Potential des Redoxsystems H2/2H3O+
H2 + 2H2O
2H3O+ + 2e-
ein.
171
Bei einer Standardwasserstoffelektrode beträgt c(H3O+) = 1 mol/l und p(H2) = 1,013 bar. Das
Standardpotential der Standardwasserstoffelektrode (auch Normalwasserstoffelektrode – Abkürzung
NHE) erhält willkürlich den Wert Null:
E° (H2/2H3O+) = 0
Das Standardpotential einer anderen elektrochemischen Elektrode (Halbzelle bzw. Redoxsystem)
erhält man durch Messung der Zellspannung eines galvanischen Elements, bei dem ein
Standardhalbelement gegen die Standardwasserstoffelektrode geschaltet ist.
Galvanisches Element
Zellspannung E° = E° (Kathode) – E° (Anode)
E° = 0,76 V = E° (H2/2H3O+) – E° (Zn/Zn2+)
Zn / Zn2+ // NHE
Cu / Cu2+ // NHE
= 0,34 V = E° (Cu/Cu2+)
– E° (H2/2H3O+)
E° (H2/2H3O+) = 0
E° (Zn/Zn2+) = - 0,76 V
E° (Cu/Cu2+) = +0,34 V
Standardpotentiale E° (=Standardredoxpotentiale) sind also Relativwerte bezogen auf die
Standardwasserstoffelektrode, deren Standardpotential willkürlich null gesetzt wurde.
Die Standardredoxpotentiale sind ein Maß für das Redoxverhalten eines Redoxsystems
(= korrespondierendes Redoxpaar) in wässeriger Lösung. Man ordnet die korrespondierenden
Redoxpaare nach der Größe ihrer Standardredoxpotentiale und erhält eine Redoxreihe, die als
Spannungsreihe bezeichnet wird:
Elektrochemische Spannungsreihe
Reduzierte
Form
Li
K
Ba
Ca
Na
Mg
Al
Mn
Zn
Cr
S2Fe
Cd
Co
Sn
Pb
Fe
H2 + 2H2O
Oxidierte
Form
Li+
K+
Ba2+
Ca2+
Na+
Mg2+
Al3+
Mn2+
Zn2+
Cr3+
S
Fe2+
Cd2+
Co2+
Sn2+
Pb2+
Fe3+
2H3O+
+ze- Standardpotential
E° in V
+ e+ e+2e+2e+ e+2e+3e+2e+2e+3e+2e+2e+2e+2e+2e+2e+3e+2e-
-3,04
-2,92
-2,90
-2,87
-2,71
-2,36
-1,68
-1,19
-0,76
-0,74
-0,48
-0,41
-0,40
-0,28
-0,14
-0,13
-0,036
0
172
Reduzierte
Form
Oxidierte
Form
H2 + 2H2O
2H3O+
Sn2+
Sn4+
Cu+
SO2 + 6H2O
Cu
Cu
2IH2O2 + 2H2O
Fe2+
Ag
Hg
NO + 6H2O
2Br6H2O
2Cr3+ + 21H2O
2ClPb2+ + 6H2O
Au
Mn2+ + 12H2O
3H2O + O2
2F-
Cu2+
SO42- + 4H3O+
Cu2+
Cu+
I2
O2 + 2H3O+
Fe3+
Ag+
Hg2+
NO3- + 4H3O+
Br2
O2 + 4H3O+
Cr2O72- + 14H3O+
Cl2
PbO2 + 4H3O+
Au3+
MnO4- + 8H3O+
O3 + 2H3O+
F2
+ze-
Standardpotential
E° in V
+2e+2e+ e+2e+2e+ e+2e+2e+ e+ e+2e+3e+2e+4e+6e+2e+2e+3e+5e+2e+2e-
0
+0,15
+0,15
+0,17
+0,34
+0,52
+0,54
+0,68
+0,77
+0,80
+0,85
+0,96
+1,07
+1,23
+1,33
+1,36
+1,46
+1,50
+1,51
+2,07
+2,87
Einteilung nach der Größe des Standardredoxpotentials
Starke Reduktionsmittel
Mittelstarke Reduktionsmittel
Schwache Reduktionsmittel
Schwache Oxidationsmittel
Mittelstarke Oxidationsmittel
Starke Oxidationsmittel
E° in V
Beispiele
< -0,6
-0,6...0
0...0,5
0,5...1,0
1,0...1,4
> 1,4
Zn, Al
Fe, Cd, Cr2+
Sn2+, H2S, S2O32Ag+, Fe3+, I2
MnO2, Cl2, Cr2O72MnO4-, S2O82-, Ag2+
Je größer das Standardredoxpotential eines korrespondierenden Paares (Red
Ox + ne-), um so geringer ist die Tendenz der Elektronenabgabe durch die
reduzierte Form Red (Abnahme der Reduktionskraft) und um so größer ist die
Tendenz der Elektronenaufnahme durch die oxidierte Form (Zunahme der
Oxidationskraft).
Ein schwaches (starkes) Reduktionsmittel steht in Verbindung (=korrespondiert)
mit einem starken (schwachen) Oxidationsmittel.
173
Mit Hilfe der Spannungsreihe lässt sich voraussagen, welche Redoxreaktionen möglich sind. Die
reduzierte Form eines Redoxsystems gibt Elektronen nur an die oxidierte Form von solchen
Redoxsystemen ab, die in der Spannungsreihe darunter stehen. Einfacher ausgedrückt: Es reagieren
Stoffe links oben mit Stoffen rechts unten (vergl. S. 1). Alle Metalle mit negativem Potential, also alle
Metalle, die in der Spannungsreihe oberhalb von Wasserstoff stehen, können Elektronen an H3O+Ionen abgeben und Wasserstoff entwickeln. Man bezeichnet diese Metalle als unedle Metalle (Fe, Zn).
Metalle mit positivem Potential, die in der Spannungsreihe unterhalb von Wasserstoff stehen, wie Cu,
Ag, Au, können sich nicht in Säuren unter H2-Entwicklung lösen und sind z. B. in HCl unlöslich. Man
bezeichnet sie daher als edle Metalle.
Es ist natürlich zu beachten, dass diese Voraussage nur aufgrund der Standardredoxpotentiale
geschieht und nur für solche Konzentrationsverhältnisse richtig ist, bei denen das aktuelle
Redoxpotential nur wenig vom Standardredoxpotential verschieden ist.
19.2
Die Konzentrationsabhängigkeit des Redoxpotentials E
Der Zusammenhang zwischen der Konzentration und dem Elektrodenpotential E eines Redoxpaares
(= Redoxpotential) wurde von Walther Nernst abgeleitet (Nernst-Gleichung)
Ox + ne-
Red
E = E° +
R T
n F
c (Ox)
c (Red)
ln
E° = Standardredoxpotential des Redoxpaares
N = Anzahl der pro Formelumsatz ausgetauschten Elektronen
R = Gaskonstante = 8,314 J  K-1  mol-1
F = Faraday-Konstante = 96490 C  mol-1
T = Temperatur in Kelvin
c(Ox) bzw. c(Red) = Konzentrationen (eigentlich Aktivitäten) aller Reaktionspartner auf der
Oxidations- bzw. Reduktionsseite. Bei Gasen wird der Partialdruck p eingesetzt.
Werden alle Variablen eingesetzt und die Gleichung in den dekadischen Logarithmus umgeformt, so
lautet die Nernst-Gleichung für eine Temperatur von 298,15K (25°C):
E = E° +
0,059
n
c (Ox)
c (Red)
lg
Mit dieser Gleichung können Elektrodenpotentiale beliebiger Redoxpaare berechnet werden, die nicht
unter Standardbedingungen {c(Ox) = 1 mol/l, c(Red) = 1 mol/l} vorliegen.
Für eine Zinkhalbzelle mit der Konzentration des Elektrolyten c(Zn2+) = 0,1 mol/l ergibt sich:
Zn (s)
Zn2+ + 2e-
E = E°(Zn/Zn2+) +
= -0,76 V +
0,059
2
E° = -0,76 V
0,059
n
lg c (Zn2+)
lg 0,1
= -0,79 V
174
Zwischen zwei Zn/Zn2+ - Halbzellen, die sich nur durch c(Zn2+) unterscheiden (eine Halbzelle c = 1
mol/l – Standardbedingungen und die andere c(Zn2+) = 0,1 mol/l – obige E-Berechnung) fließt ein
Strom von der Halbzelle mit der niedrigeren Zn2+-Konzentration zur Halbzelle mit der höheren Zn2+Konzentration, da ein Potentialgefälle besteht.
E = E° (Zn/Zn2+) - E(Zn/Zn2+ [c = 0,1 mol/l])
= -0,76 V
- (-0,79 V)
= 0,03 V
Je kleiner die Zinkionen-Konzentration in einer Lösung ist, um so größer wird die reduktive Kraft von
metallischem Zink (z. B. Zink-Granalien).
Das obige Rechenbeispiel zeigt aber auch, dass die Abweichungen von den Standardkonzentrationen
schon mehrere Zehnerpotenzen betragen muss, um eine deutliche Abweichung von den
Standardredoxpotentialen zu bewirken. Für die Einschätzung vieler Redoxreaktionen sind deshalb die
Standardredoxpotentiale der Spannungsreihe ausreichend.
Deutliche Abweichungen von den Standardredoxpotentialen werden z. B. hervorgerufen, wenn
a)
b)
die reduzierte Form und/oder die oxidierte Form des Redoxpaares an der Bildung einer
schwerlöslichen Verbindung oder einer Komplexverbindung und
Protonen an der Halbzellenreaktion beteiligt sind
zu a)
Zu diesem Punkt werden Bespiele bei der Behandlung der Übergangsmetallchemie
besprochen.
zu b)
pH-Abhängigkeit von Redoxpotentialen
)
H2 + 2H2O
2H3O+ + 2e-
c(H3O+) = 1 mol/l
E° = 0 V
Beim Redoxpaar (H2/2H3O+) ergibt sich die Veränderung des Redoxpotentials mit der
H3O+-Konzentration beim Wasserstoffdruck von 1,013 bar aus der Beziehung:
0,059
n
E = E°(H2/2H3O+) +
= 0 +
0,059
2
lg
lg
c2 (H3O+)
p (H2)
c2(H3O+)
1
~
~ 0,03 lg c2(H3O+)
in saurem Wasser c(H3O+)
in neutralem Wasser c(H3O+)
in basischem Wasser c(OH-)
= 1 mol/l
= 10-7 mol/l
= 1 mol/l
(pH = 0)
(pH = 7)
(pH = 14)
E= 0V
E = -0,41 V
E = -0,82 V
Dementsprechend lassen sich z. B. die H3O+ -Ionen des neutralen Wassers thermodynamisch nur durch
solche Metalle zu H2 entladen, deren Potential < -0,41 V ist, z. B. durch Alkali- und Erdalkalimetalle.
Die Zahl der zur Darstellung von Wasserstoff aus Wasser geeigneten Metalle ist also kleiner als die
zur H2-Gewinnung aus Säuren in Frage kommende Zahl von Metallen mit einem Potential < 0 V.
175
Die Tatsache, dass Stoffe wie Magnesium, Aluminium oder Zink mit Wasser entgegen ihrer Stellung
in der Spannungsreihe keinen Wasserstoff entwickeln, beruht darauf, dass das bei der Umsetzung
Mg(OH)2 + H2 )
gebildete unlösliche Metallhydroxid (z. B. Mg + 2H2O
eine Schutzschicht um das Metall bildet, welche den weiteren Angriff des Wassers verhindert, so dass
die Reaktion gleich nach Beginn zum Stillstand kommt. Löst man die Hydroxidschicht durch Zugabe
z. B. von Säure auf, so geht die H2-Entwicklung weiter. Metalle wie die Alkali- oder schweren
Erdalkalimetalle, die lösliche Hydroxide bilden, können keine solche Schutzschicht ausbilden und
reagieren daher mit Wasser lebhaft unter H2-Entwicklung.
) Auch bei einer Reihe anderer Redoxsysteme, bei denen H3O+-Ionen auftreten, sind die Potentiale
sehr stark vom pH-Wert abhängig, und das Redoxverhalten solcher Systeme kann nicht mehr aus den
Standardredoxpotentialen allein vorausgesagt werden.
z.B.
12H2O + Mn2+
E = E° +
0,059
5
MnO4- + 8H3O+ + 5e-
lg
c(MnO4-) c8(H3O+)
c(Mn2+)
E° = 1,51 V
Im Zähler des konzentrationsabhängigen Teils der Nernstschen Gleichung stehen die Produkte der
Konzentrationen der Teilchen der oxidierenden, im Nenner die Produkte der Konzentrationen der
Teilchen der reduzierenden Seite des Redoxsystems.
Berechnet man E unter Annahme der Konzentrationen c(MnO4-) = 0,1 mol/l und c(Mn2+) = 0,1 mol/l,
so erhält man für verschiedene saure Lösungen:
pH
c(H3O+) [mol/l]
E[V]
0
5
7
1
10-5
10-7
1,51
1,04
0,85
Die Oxidationskraft von MnO4- verringert sich also stark mit wachsendem pH.
19.3
Aufstellen von Redoxgleichungen
Das Behelfsmodell Oxidationszahl vereinfacht die Beschreibung von Redoxreaktionen:
Eine Oxidation ist eine Erhöhung der Oxidationszahl.
Eine Reduktion ist eine Erniedrigung der Oxidationszahl.
Regeln zur Ermittlung von Oxidationszahlen (OZ):
0 0 0 0
Cl2, He, S8, P4
1)
Elemente haben die OZ = 0
2)
Für einfache Ionen ist die OZ gleich der Ionenladung
-I -II +II +III
Cl-, O2-, Fe2+, Al3+
176
3)
Oxidationszahlen der Elemente in Verbindungen werden so ermittelt, dass
Bindungselektronen dem elektronegativeren Bindungspartner zugeteilt werden.
+I
-I
H - Cl
Cl
χ 2,8
die
H
2,2
Die Summe aus positiven und negativen Oxidationszahlen muss gleich der Ladung des Moleküls sein.
a)
b)
c)
Fluor (als elektronegativstes Element) hat stets die OZ = -I
Metalle erhalten in ihren Verbindungen stets positive OZ
Wasserstoff hat in seinen Verbindungen die OZ = +I, es sei denn, eine der vorstehenden
Regeln greift:
+I -I
Na H
d)
Sauerstoff hat meist die OZ = -II
(Ausnahmen:
+I -I -I -I
H - O - O - H,
Beispiele:
-II +IV -II
O=C=O
+II-I
OF2)
+VII -II
MnO4-
+I+V-II
H3 P O4 (Phosphorsäure)
4)
a)
b)
c)
Sonderregeln für Oxidationszahlen von C-Atomen in organischen Verbindungen:
Zahlwert
Bindung zu C
0
Bindung zu elektronegativerem Partner
(O, N, S, Halogen) oder negative Ladung
Doppelbindung (O, N, S)
+I
+II
Bindung zu elektropositivem Partner (H)
-I
Beispiele:
H H
H
-III
C
-I
C
H
O H
H
H H
-III
+I
C C
H
O
H
Aufstellen der Redoxgleichung (Methode der Halbreaktionen):
Beispiel: Cl2-Darstellung (Oxidation von Salzsäure mit Kaliumpermangant)
1.
Edukte und Produkte werden ohne Berücksichtigung der Stöchiometrie aufgeführt:
HCl + KMnO4
Cl2 + MnCl2
177
„Zuschauer-Ionen“ werden eliminiert und die verbleibenden Teilchen mit Oxidationszahlen
versehen.
-I +VII
HCl + MnO4-
0
+II
Cl2 + Mn2+
2.
Oxidations- und Reduktions-Halbreaktion
stöchiometrisch korrekt
a)
b)
hinsichtlich der Anzahl der transferierten Elektronen
aller Atomzahlen (z. B. von H und O; Hinzufügen von H+ und H2O, wenn die Reaktion im
sauren Medium abläuft; oder H2O und OH-, wenn die Reaktion in einem basischen Medium
abläuft).
Oxidation:
Reduktion:
3.
-I
2HCl
+VII
MnO4- + 8H+ + 5e-
10 HCl
Reduktion x 2: 2 MnO4- + 16H+ + 10e-
formuliert,
und
zwar
0
Cl2 + 2 H+ + 2e-
+II
Mn2+ + 4H2O
5 Cl2 + 10 H+ + 10e2 Mn2+ + 8 H2O
Addition der Halbreaktionen und Kürzen der Spezies, die auf beiden Seiten der Gleichung
auftreten:
10 HCl + 2 MnO4- + 6H+
5.
getrennt
Die Halbreaktionen werden mit Koeffizienten multipliziert, so dass die Zahl der bei jeder
Halbreaktion transferierten Elektronen dieselbe ist.
Oxidation x 5:
4.
werden
5 Cl2 + 2 Mn2+ + 8 H2O
Hinzufügen der “Zuschauer-Ionen”
16 HCl + 2 KMnO4
5 Cl2 + 2 MnCl2 + 8 H2O + 2 KCl