Funktionenfolgen

KAPITEL 4
Funktionenfolgen
1. Punktweise Konvergenz und gleichmäßige Konvergenz
Definition 4.1 (Funktionenfolgen). Gegeben sei I ⊂ R und zu jedem n ∈ N
eine Funktion fn : I → R. Die numerierte Menge der Funktionen fn , n ∈ N
heißt Funktionenfolge und wird mit (fn )n∈N bezeichnet.
Definition 4.2 (Punktweise Konvergenz). Die Funktionenfolge (fn )n∈N heißt
Punktweise konvergent gegen eine Funktion f : I → R falls die Folge
(fn (x))n∈N für jedes x ∈ I gegen f (x) konvergiert.
Definition 4.3 (Gleichmäßige Konvergenz). Die Funktionenfolge (fn )n∈N heißt
gleichmäßig konvergent gegen eine Funktion f : I → R falls dn :=
supx∈I |fn (x) − f (x)| gegen Null konvergiert.
Satz 4.4. Ist fn : I → R für jedes n ∈ N stetig und konvergiert (fn )n∈N
gleichmäßig gegen f : I → R, so ist f stetig.
Satz 4.5. Ist fn : [a, b] → R für jedes n ∈ N stetig und ist (fn )n∈N gleichmäßig
Rb
konvergent gegen eine Funktion f : I → R, so gilt limn→∞ a fn (x) dx =
Rb
a f (x) dx.
Satz 4.6. Ist I ⊂ R offen und fn : I → R für jedes n ∈ N stetig differenzierbar.
Ist die Funktionenfolge (fn )n∈N punktweise konvergent gegen eine Funktion f :
I → R und ist die Funktionfolge (fn′ )n∈N gleichmäßig konvergent gegen eine
Funktion f˜ : I → R, so ist f differenzierbar und (fn′ )n∈N konvergiert gegen f ′ .
27
2. Potenzreihen
Definition 4.7 (Potenzreihen). Es sei (an )n∈N eine Folge und x0 ∈ R.
Durch (an )n∈N und x0 werde eine Funktionenfolge (fn )n∈N aus Polynomen
Pn
k definiert. Den Grenzwert für n → ∞ , also
fn (x) =
k=0 ak (x − x0 ) P
P
∞
n
k
k
k=0 ak (x − x0 ) := limn→∞
k=0 ak (x − x0 ) , nennt man Potenzreihe. Die
Zahlen ak ∈ R nennt man Koeffizienten, die Zahl x0 den Entwicklungspunkt der Potenzreihe. Die Menge
I := {x ∈ R | (fn (x))n∈N ist konvergent}
heißt Konvergenzbereich der Potenzreihe.
P∞
k
Satz 4.8. Es sei (ak )k∈N eine Folge und
k=0 ak (x − x0 ) die dazugehörige
Potenzreihe. Es gilt:
a) Es gibt einen Wert R ∈ {0} ∪ R ∪ {+∞} (den sogenannten Konvergenzradius) mit den Eigenschaften:
P
(i) Ist |x − x0 | < R so ist ∞
ak (x − x0 )k konvergent.
Pk=0
k
(ii) Ist |x − x0 | > R so ist ∞
k=0 ak (x − x0 ) divergent.
|ak |
uneigentlich (d.h.
b) Existiert der Grenzwert limk→∞ |ak+1 |
|ak |
k|
limk→∞ |a|ak+1
| ∈ R ∪ {∞} so ist R = limk→∞ |ak+1 | .
c) Es gilt
p

0
falls ( k |ak |)k∈N unbeschränkt


p
1 √
falls
lim supk→∞ k |ak | ∈ R+
R=
k
lim
sup
|a
|
k
k→∞

p

∞
falls
lim supk→∞ k |ak | = 0
p
k
|ak | der größte Häufungspunkt der Folge
Hierbei
ist
lim
sup
k→∞
p
k
( |ak |)k∈N .
d) Auf jedem abgeschlossenen Intervall [a, b] ⊂]x0 −R, x0 +R[ konvergiert
P
die Funktionenfolge (fn )n∈N , fn : [a, b] → R, fn (x) = nk=0 ak (x−x0 )k
gleichmäßig.
P
k
Satz 4.9. Ist ∞
k=0 ak (x − x0 ) eine Potenzreihe mit Konvergenzradius R, so
gilt für die Funktion
∞
X
f :]x0 − R, x0 + R[→ R, x 7→
ak (x − x0 )k
k=0
P∞
)k−1
a) Die Potenzreihe k=0 kak (x − x0
hat Konvergenzradius R und es
P
k−1 .
gilt f ′ (x) = ∞
ka
(x
−
x
)
0
k=0P k
∞
ak
(x
− x0 )k+1 hat Konvergenzradius R und
b) Die Potenzreihe
k=0
k+1
P ∞ ak
k+1
F (x) = k=0 k+1 (x − x0 )
ist eine Stammfunktion von f .
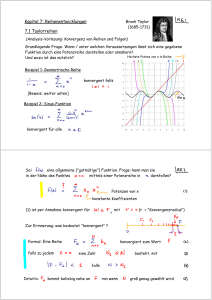
3. Taylorreihen
Definition 4.10 (Taylorpolynom und Taylorreihe). Sei f : I → R eine n-mal
differenzierbare Funktion, I offen und p ∈ I. Das Polynom
n
X
f (k) (p)
Tn (x) :=
(x − p)k
k!
k=0
heißt Taylorpolynom von f im Entwicklungspunkt p. Ist f beliebig oft differen(k)
P
zierbar, so nennt man die Reihe nk=0 f k!(p) (x−p)k Taylorreihe von f im Punkt
p.
Satz 4.11. Sei f : I → R eine n-mal differenzierbare Funktion, M ⊂ I offen
und p ∈ M . Das Taylorpolynom Tn ist das einizige Polynom vom Grad n mit
der Eigenschaft
Tn(k) (p) = f (k) (p), k = 1, . . . , n.
Satz 4.12 (Satz von Taylor). Sei f : I → R eine n + 1-mal differenzierbare
Fuktion, I ein offens Intervall und p ∈ M . Zu jedem x ∈ I \ {p} gibt es ein ξ
zwischen x und p so dass
f (x) = Tn (x) + Rn,x
mit
Rn,x =
f (n+1) (ξ)
· (x − p)n+1
(n + 1)!
gilt.
Satz 4.13. Sei f : I → R eine beliebig oft differenzierbare Fuktion, I ein offenes
Intervall und p ∈ I. Gibt es Zahlen M > 0 und C > 0 so dass |f (n) (x)| ≤ M ·C n
für alle n ∈ N und alle x ∈ I gilt, so ist
∞
X
f (k) (p)
(x − p)k
f (x) =
k!
k=0
für alle x ∈ I.
Satz 4.14. Für alle x ∈ R gilt
∞
∞
X
X
(−1)k x2k+1
(−1)k x2k
sin(x) =
und cos(x) =
.
(2k + 1)!
(2k)!
k=0
k=0