Kapitel 7: Reihenentwicklungen 7.1 Taylorreihen

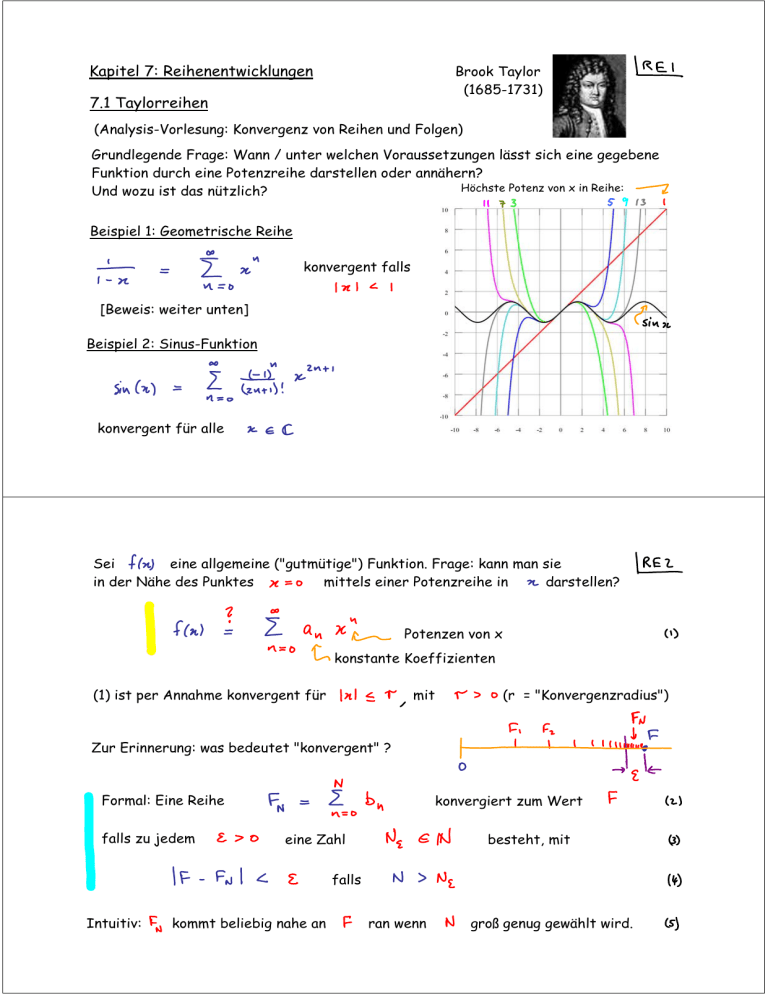
Kapitel 7: Reihenentwicklungen
Brook Taylor
(1685-1731)
7.1 Taylorreihen
(Analysis-Vorlesung: Konvergenz von Reihen und Folgen)
Grundlegende Frage: Wann / unter welchen Voraussetzungen lässt sich eine gegebene
Funktion durch eine Potenzreihe darstellen oder annähern?
Höchste Potenz von x in Reihe:
Und wozu ist das nützlich?
Beispiel 1: Geometrische Reihe
konvergent falls
[Beweis: weiter unten]
Beispiel 2: Sinus-Funktion
konvergent für alle
Sei
eine allgemeine ("gutmütige") Funktion. Frage: kann man sie
in der Nähe des Punktes
mittels einer Potenzreihe in
darstellen?
Potenzen von x
konstante Koeffizienten
(1) ist per Annahme konvergent für
mit
(r = "Konvergenzradius")
Zur Erinnerung: was bedeutet "konvergent" ?
Formal: Eine Reihe
falls zu jedem
konvergiert zum Wert
eine Zahl
besteht, mit
falls
Intuitiv:
kommt beliebig nahe an
ran wenn
groß genug gewählt wird.
Angewandt auf (2.1): mit
[für ein gegebenes
]:
Die Reihe
falls zu jedem
konvergiert zum Wert
eine Zahl
besteht, mit (siehe 2.4)
falls
"Restglied"
Bestimmung der Koeffizienten
:
Grundidee: wähle die
so, dass sich
möglichst eng an
"anschmiegt", d.h. dass alle Ableitungen beider Funktionen bei
gleich sind.
Gliedweises Differenzieren: (!?! macht nur Sinn, falls Reihe konvergiert!)
(n = 0 fällt weg)
(nur n=1 trägt bei)
(n = 1 fällt weg)
(nur n=2 trägt bei)
Per Induktion gilt
für allgemeines n:
Reihenentwicklung
v. f(x):
"Taylor-Reihe"
Nochmal Beispiel 1: (jetzt explizit)
"n Fakultät"
Satz von Taylor:
Sei
ein Interval,
,
und
eine (N+1)-mal stetig differenzierbare
Funktion. Dann gilt für
:
mit Restglied
mit
Beweis: durch Induktion (Analysis-Vorlesung; z.B. Otto Forster, "Analysis 1")
[Das Restglied kann auch auf verschiedene andere Weisen ausgedrückt werden.]
Folgerungen:
(i) Die Taylorreihe (4.7) konvergiert gegen
falls
für
(ii) Falls Taylorreihe (4.7) konvergiert, ist das Restglied für Ordnung N gegeben durch
(iii) Geometrische Interpretation: sukzessive Approximation durch Polynome
[siehe auch Skizze für sin(x), Seite 1]
-te Approximation: Konstante
-te Approximation: Gerade
-te Approximation: Parabel
-te Approximation: Polynom
-ten Grades
(iv) Verschiebung des Entwicklungspunktes:
wird zu
(v) Falls Taylorreihe konvergiert, ist gliedweises Differenzieren / Integrieren
innerhalb des Konvergenzradius erlaubt.
Beispiel 3:
Nutze Taylor-Entwicklung (5.7):
gilt nur für
Beachte: da Taylorreihe für
nicht konvergiert, liefern höhere
Taylorterme
dort eine
zunehmend schlechtere Näherung!
(vi) Manche spezielle Funktionen lassen sich über eine Taylor-Reihe definieren:
Exponentialfunktion:
http://en.wikipedia.org/wiki/Taylor_series
Definierende
Eigenschaften:
(4.7):
(8) in (4.7):
überall im Komplexen
konvergent, d.h. für alle
(10) kann als alternative Definition der Exp-Funktion aufgefasst werden.
Sinus und Cosinus:
Bekannte Eigenschaften:
Wert bei Null:
Ableitung:
Eigenschaften (1)-(6) bestimmen die Reihenentwicklungen v. sin und cos eindeutig:
(1) und (2) können als alternative Definitionen der Trig-Funktionen aufgefasst werden.
(1) und (2) sind konvergent für alle
Betrachte:
n = gerade
n = ungerade
Euler - de Moivre Identität
Wir wissen aus geometrischer Definition der Trig-Funktionen:
Euler-Identität
Vereint die 5 wichtigsten Zahlen,
in einer Gleichung!