Zahlen - Die Onleihe

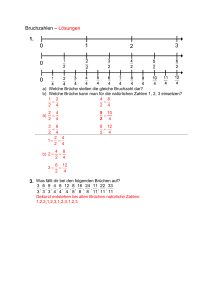
Inhalt
Vorwort
7
1. Natürliche Zahlen 9
1.1 Zählen 9
1.2 Eigenschaften von Zahlen 11
1.3 Magische Quadrate 16
1.4 Primzahlen 19
1.5 Von Pythagoras zu Fermat 23
1.6 Was sind natürliche Zahlen? 27
1.7 Anwendung: Kryptographie 31
2. Zahlendarstellungen 36
2.1 Wie hat man früher Zahlen geschrieben?
2.2 Abakus und Rechentisch 39
2.3 Das Dezimalsystem 45
2.4 Teilbarkeitsregeln 48
2.5 Binärzahlen 52
2.6 Anwendung: Strichcodes 54
36
3. Rational und irrational 57
3.1 Gebrochene Zahlen 57
3.2 Verhältnisse 60
3.3 Rationale Zahlen 65
3.4 Irrationale Zahlen – die erste Krise der Mathematik
3.5 Dezimalbrüche 75
4. Transzendente Zahlen 79
4.1 Die geheimnisvollste Zahl 79
4.2 Grenzwerte 83
4.3 Wie viele transzendente Zahlen gibt es?
90
70
5. Imaginär und komplex 96
5.1 Lineare Gleichungen 97
5.2 Quadratische Gleichungen 98
5.3 Das Drama um die Gleichung dritten Grades 102
5.4 Die Tragödie um die Gleichung fünften Grades 105
5.5 Alle Gleichungen sind lösbar! 107
Literatur
112
3.3 Rationale Zahlen
65
101 = 2 · 35 + 31
35 = 1 · 31 + 4
31 = 7 · 4 + 3
4=1·3+1
3=3·1
Mit Hilfe des euklidischen Algorithmus kann man den größten
gemeinsamen Teiler auch sehr großer Zahlen leicht berechnen,
ohne die Primfaktorzerlegung dieser Zahlen kennen zu müssen.
Diese Technik spielt in vielen Anwendungen eine Schlüsselrolle,
zum Beispiel in der modernen Kryptographie (siehe Kapitel 1).
3.3 Rationale Zahlen
Natura non facit saltus.
Bruchzahlen kann man auf verschiedene Weise einführen: als
Anteile, als Bruchteile oder als Verhältnisse. Wenn man heutige
Schulbücher aufschlägt, sieht man unterschiedlichste Modelle
für Bruchzahlen: Kuchen- oder Pizzateile, Teile von Rechtecken
oder von Strecken.
Für Bruchzahlen hat sich auch der Begriff «rationale Zahlen»
eingebürgert. Diese Bezeichnung kommt vom lateinischen Wort
ratio, welches unter anderem «Verhältnis» bedeutet. «Rationale
Zahlen» sind vom Wortsinn her also Verhältniszahlen, bedeuten aber das Gleiche wie Bruchzahlen.
Auch ganze Zahlen sind Bruchzahlen, denn man kann die
Zahl 5 natürlich auch als ⁄ schreiben. Das heißt: Die Menge
der ganzen Zahlen ist in der Menge der Bruchzahlen enthalten.
Mit rationalen Zahlen kann man wunderbar rechnen; als Rechengrößen lassen sie kaum einen Wunsch offen: Man kann addieren, subtrahieren, multiplizieren und dividieren. Und das
geht so gut, wie man sich das nur wünschen kann.
Addieren und Subtrahieren von rationalen Zahlen ist besonders einfach, jedenfalls wenn man sich eine rationale Zahl als
Strecke, als «Kuchenstück» oder als eine andere geeignete Größe vorstellt. Um ⁄ + ⅜ zu bestimmen, betrachten wir zum Beispiel eine Strecke der Länge ⁄ und eine Strecke der Länge ⅜
66
3. Rational und irrational
und fügen dann die beiden Streckenstücke aneinander. Das Ergebnis ist eine Strecke der Länge ⁄ + ⅜.
Schwierig wird diese Aufgabe erst dann, wenn wir das Ergebnis ⁄ + ⅜ wieder als Bruch darstellen wollen. Dafür macht
man sich zunächst eine einfachere Aufgabe klar: Wenn zwei
Brüche den gleichen Nenner haben, ist die Addition einfach: ein
Fünftel plus drei Fünftel sind vier Fünftel. Man tut dabei so, als
wenn «Fünftel» eine Objektbezeichnung wäre, so etwas wie
Äpfel oder Pizza. Ein Fünftel einer Pizza plus zwei Fünftel einer
Pizza sind natürlich drei Fünftel einer Pizza.
Wie löst man nun ⁄ + ⅜? Hier kommt die wunderbare Eigenschaft der Bruchzahlen zum Einsatz, dass sich nämlich die
gleiche Bruchzahl durch verschiedene Brüche darstellen lässt.
Klar, ⁄ ist das Gleiche wie ½, ⁄ das Gleiche wie ⅜. Mit
anderen Worten: Man kann Brüche erweitern, indem man Zähler und Nenner mit der gleichen Zahl multipliziert – und die
Bruchzahl verändert sich beim Erweitern nicht.
Beim Addieren von zwei Brüchen erweitert man beide Brüche
so, dass sie den gleichen Nenner haben. In der Schule sagt man
dazu: Man bringt sie auf den «Hauptnenner»: In unserem Beispiel ist ⁄ = ⁄ (Erweiterung mit 8) und ⅜ = ⁄ (Erweiterung mit 7). Also gilt ⁄ + ⅜ = ⁄ + ⁄. Da diese Brüche den
gleichen Nenner haben, kann man deren Summe bestimmen:
⁄ + ⁄ = ⁄.
Bei der Addition von Brüchen kann man sehr großzügig vorgehen. Man darf die Reihenfolge vertauschen: ½ + ⅓ ist das Gleiche wie ⅓ + ½. Addiert man mehr als zwei Brüche, will man
zum Beispiel wissen, was ⅓ + ¼ + ⅛ ist, dann darf man sich
aussuchen, welches der beiden Pluszeichen zuerst ausgeführt
wird. Man könnte zuerst ⅓ + ¼ rechnen (das ergibt ⁄) und
dann ⅛ dazuaddieren. Das ist ⁄ + ⁄, also ⁄. Man könnte aber auch zunächst das zweite Pluszeichen ausführen (also
¼ + ⅛ = ⅜ rechnen) und dann ⅓ dazuaddieren. Es ergibt sich
⁄ + ⁄ = ⁄. Egal, wie man rechnet, es kommt das Gleiche
raus!
Diese Eigenschaften heißen Kommutativgesetz und Assozia-
3.3 Rationale Zahlen
67
tivgesetz. Ich finde den Begriff «Gesetz» hier irreführend, denn
bei Gesetzen denken wir an Einschränkungen. Es handelt sich
aber um Möglichkeiten der Freiheit. Sie können sich Ihre Reihenfolge bei der Addition von gewissen Bruchzahlen wählen,
ich kann mir meine aussuchen – und beide werden wir das gleiche Ergebnis erhalten!
Produkte und Quotienten von Bruchzahlen sind schwieriger
vorzustellen, und das liegt nicht an den Brüchen. Die Griechen
hatten sich Zahlen immer als Streckenlängen gedacht. Dann ist
klar, was Strecke mal Strecke sein soll, nämlich eine Fläche. Aus
einer Strecke mit 4 und einer mit 5 Längeneinheiten erhält man
als Produkt ein Rechteck mit 20 Flächeneinheiten.
Das klingt gut, birgt aber eine fatale Schwierigkeit in sich.
Das Produkt ist nämlich prinzipiell etwas ganz anderes als die
einzelnen Faktoren – eine Fläche. Das Produkt aus drei Strecken
ist ein Volumen, und ein Produkt aus vier Strecken ist nicht
mehr vorstellbar.
Auch beim Teilen führt diese Vorstellung zu Schwierigkeiten.
Was ist 12 geteilt durch 3? Um diese Aufgabe zu lösen, kann
man sie auf verschiedene Weise interpretieren:
(a) Gegeben sei ein Rechteck mit dem Flächeninhalt 12. Wenn
eine Seitenlänge die Länge 3 hat, wie lang ist dann die andere?
Achtung: Jetzt muss man eine Zahl als Flächeninhaltszahl
auffassen!
(b) Wie oft passt eine Strecke der Länge 3 in eine Strecke der
Länge 12? Die Antwort ist einfach: 4 Mal.
Achtung: Jetzt ist das Ergebnis eine Anzahl und keine Streckenlänge!
Den gedanklichen Durchbruch schaffte René Descartes
(1596–1650), der Erfinder der Analytischen Geometrie, also
der Geometrie, in der mit Koordinaten gerechnet wird. Zur
Multiplikation schreibt er: «Es sei zum Beispiel AB die Einheit
und es wäre BD und BC zu multiplizieren, so habe ich nur die
Punkte A und C zu verbinden, dann DE parallel mit CA zu ziehen und BE ist das Product der Multiplication.»
Um die Strecke BC mit der Strecke AD zu multiplizieren, wählt
68
3. Rational und irrational
Multiplikation von Strecken nach Descartes
man zunächst A so, dass BA die Länge 1 hat, und konstruiert
dann den Punkt E so wie beschrieben. Nach dem sogenannten
ersten Strahlensatz ist dann
.
Wegen BA = 1 folgt daraus BE = BD · BC. Also Strecke mal Strecke = Strecke! Nun kann man beliebig viele Zahlen miteinander
multiplizieren und es kommt immer eine Streckenlänge heraus!
Diese Einsicht hat viel zum abstrakten Zahlenbegriff beigetragen. Denn wenn sowohl die Faktoren als auch das Produkt
Strecken sind, dann ist es naheliegend, die Streckenlängen irgendwann zu vergessen und nur noch an Zahlen zu denken.
Die Regeln für Multiplikation und Division von Bruchzahlen
sind als Regeln einfach, aber nicht ganz einfach zu verstehen.
⅔ · ½ ist einfach auszurechnen. Man multipliziert die Nenner
und die Zähler, somit ergibt sich als Produkt ˙⁄˙, also ⁄, und
das ist ⅓.
Wie lässt sich das erklären? Hier hilft eine sorgfältige sprachliche Formulierung. Die Aufgabe ⅔ · 6 kann als «⅔ von 6» beschrieben werden, und dann ist klar, dass sich 4 ergibt. Entsprechend lautet die Aufgabe ⅔ · ½ in sprachlicher Form «⅔ von
½», und dann wird auch klar, dass das Ergebnis ⁄ ist. (Man
teilt ½ in drei Sechstel; ⅔ davon sind dann zwei Sechstel.)
3.3 Rationale Zahlen
69
Die Division durch eine Bruchzahl ist noch schwieriger vorzustellen. Betrachten wir zunächst die Aufgabe 3 : ½. Die Frage, die uns dieses Rätsel löst, heißt: Wie oft passt ½ in 3? Das ist
einfach zu beantworten: 6 Mal. Also ist 3 : ½ = 6.
Damit ist auch die Frage ⅔ : ½ zu lösen: Wie oft passt ½
in ⅔? Gleichwertig dazu kann man fragen: Wie oft passt ⁄
in ⁄? Oder entsprechend, wie oft passt 3 in 4? Antwort: genau
¾ Mal.
Division lässt sich demnach auf Multiplikation zurückführen: Durch einen Bruch zu dividieren ist das Gleiche
wie mit seinem Kehrwert zu multiplizieren. Das heißt, wenn
man durch ⅔ dividieren möchte, kann man genauso gut
mit dem Kehrwert, also ⁄, multiplizieren. Zum Beispiel:
½ : ⅔ = ½ · ⁄ = ⁄˙ = ¾.
Im Mittelalter hatte sich praktisches Rechnen mit Brüchen etabliert. De facto hatte man akzeptiert, dass ⅔ nicht nur ein Verhältnis ganzer Zahlen ist, sondern auch eine Zahl neuen Typs.
In der mathematischen Theorie wurde diese Erfahrung aber
erst viel später aufgegriffen. Erst in der Mitte des 19. Jahrhunderts entwickelte Bernard Bolzano (1781–1848) in seiner Reinen Zahlenlehre eine «Theorie der Zahlenmenge, die gegenüber
den vier Grundrechenarten abgeschlossen ist». Bolzano sah den
Begriff einer Zahl von den Rechenoperationen her: Eine sinnvolle Zahlenmenge muss die natürlichen Zahlen enthalten und
so geartet sein, dass man je zwei Zahlen addieren, subtrahieren,
multiplizieren und dividieren kann (ausgeschlossen ist allein,
durch 0 zu teilen), und in jedem Fall muss sich wieder eine Zahl
ergeben. Bolzano sagt, dass man erst Zahlen (Plural!) definieren
müsse, um sagen zu können, was eine Zahl (Singular!) ist. Sein
Hauptkriterium dafür, dass man die Elemente dieser Menge
«Zahlen» nennt, ist, dass sich damit problemlos und ohne Einschränkungen rechnen, das heißt addieren und substrahieren,
multiplizieren und dividieren, lässt. Mathematiker nennen eine
solche Struktur einen «Körper» und sprechen zum Beispiel vom
«Körper der rationalen Zahlen».
Das ist der mathematische Aspekt. In der Praxis wurden rati-