Vorbereitung KA ABI

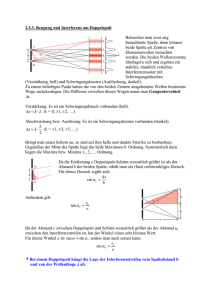
Comptoneffekt
Bestrahlt man eine Graphitprobe mit Röntgenlicht, so tritt u. a. Compton-Streuung auf.
a) Erklären Sie den Compton-Effekt mit einer Modellvorstellung. Warum ist der
Compton-Effekt bei Verwendung weicher Röntgenstrahlung nur schwer
nachzuweisen? (6BE)
b) Geben Sie eine Möglichkeit zur Messung der Wellenlänge harter monochromatischer
Röntgenstrahlung an. (2BE)
Für die weiteren Teilaufgaben sei die Energie der eingestrahlten Photonen gleich der
Ruheenergie eines Elektrons. Die Streustrahlung unter dem Winkel  = 120° wird
untersucht.
c) Stellen Sie für diesen Fall die Wellenlänge  ' und den Impulsbetrag p' der gestreuten
Photonen als Vielfache von entsprechenden Größen der einfallenden Strahlung
dar.[zur Kontrolle:  ' = 2,5· ] (5 BE)
d) Zeichnen Sie das Impulsvektordiagramm. Wählen Sie 5 cm für die Länge des
Impulsvektors der Primärstrahlung (5 BE)
e) Bestimmen Sie die kinetische Energie des Rückstoßelektrons als Vielfaches der
Ruheenergie eines Elektrons.[zur Kontrolle: Wkin = 0,60 · M0c2] (5 BE)
f) Berechnen Sie relativistisch die Geschwindigkeit des Rückstoßelektrons. (6 BE)
Lösung CD
Ph 12
Musteraufgaben
Comptoneffekt und
Rückstoßelektron
Lösung
nach LK-Abitur-Bayern 1997/III/3
a) Man erklärt sich den Comptoneffekt als vollelastischen Stoß zwischen einem Photon
und einem freien Elektron. Dabei gilt der Energiesatz und der vektorielle Impulssatz.
Die maximale Wellenlängenänderung beim Comptoneffekt ist 2 · c = 4,8·10-12 m.
Dies ist gegenüber der Wellenlänge von weichem Röntgenlicht, die bei 10-10 m liegt
so klein, dass man den Unterschied kaum messen kann.
b) Die Wellenlänge harten Röntgenlichts misst man mit der braggschen
Drehkristallmethode bei bekanntem Netzebenenabstand.
c)
d)
e)
f)
Bragg, De Broglie, Debey-Scherrer-Streuung
Materiewellen wurden 1924 postuliert und kurze Zeit später mit Versuchen wie dem DebeyScherrer-Verfahren nachgewiesen.
In einer Vakuumröhre treffen Elektronen, die aus einem Glühdraht (Heizspannung UH) ausgetreten
sind und durch die Spannung UB beschleunigt wurden, auf ein Pulver aus Graphitkristallen.
Dahinter werden sie auf einem Leuchtschirm sichtbar gemacht. Typischerweise beobachtet man
um einen hellen Mittelpunkt konzentrische, helle Kreisringe.
a) Leiten Sie anhand geeigneter Skizzen den Zusammenhang zwischen der Wellenlänge einer
auftreffenden Welle und ihren möglichen Ablenkwinkeln bei der Beugung am Einkristall her
(Bragg-Bedingung) und erklären Sie damit das Zustandekommen des beobachteten Bildes.
b) Wie kann man experimentell nachweisen, dass die gezeigten Erscheinungen tatsächlich von
Elektronen erzeugt werden und nicht von Röntgenstrahlung, die beim Auftreffen von Elektronen
auf das Pulver entstanden sein könnte?
Bei den konzentrischen Kreisen handelt es sich um Beugungen an zwei verschiedenen
Netzebenen des Graphits mit den Netzebenenabständen d1 = 1,23·10-10m und d2 = 2,13·10-10m.
Der kreisförmige Leuchtschirm (Radius R = 4,7cm) hat von der Graphitpulverschicht den Abstand
L = 13,5cm. Die Beschleunigungsspannung UB ist auf 4,0kV eingestellt.
c) Berechnen Sie relativistisch die de-Broglie-Wellenlänge l eines anfangs ruhenden Elektrons,
welches die Beschleunigungsspannung UB durchlaufen hat.
[zur Kontrolle: λ = 1,9·10-11m]
d) Bestimmen Sie, wie viele Kreise bei diesem Versuch theoretisch auf dem Leuchtschirm zu
erwarten sind.
e) Beschreiben und erklären Sie, wie sich das Bild auf dem Schirm verändert, wenn man zum
einen die Spannung UH bzw. zum anderen die Spannung UB vergrößert.
f) Zeigen Sie für den Fall kleiner Beschleunigungsspannungen (nichtrelativistischer Ansatz), dass
für den Zusammenhang zwischen der Beschleunigungsspannung UB und der de-BroglieWellenlänge λ gilt:
Bestimmen Sie damit die kleinstmöglich Beschleunigungsspannung UB, ab der theoretisch
überhaupt Interferenzkreise auf dem Leuchtschirm zu erwarten sind.
Lösung Leifi
Torwart Heisenberg
Ein Fußballspieler schießt den Ball zwischen zwei gegnerischen Verteidigern hindurch
auf das Tor. Die Masse des Balls ist m = 0,40kg, seine Geschwindigkeit v = 30m/s und
der Abstand der beiden Verteidiger Δx = 1,0m. Zeigen Sie durch eine Rechnung, dass
die Ausrede des Torwarts, er habe den Ball nicht fangen können, weil der den Impuls
nicht genau abschätzen konnte, faul ist.
Lösung Leifi
http://www.bekphysik.de/Lk13/Aufgaben/Quanten/Bragg%20De%20Broglie%20Doppelspa
lt%20%20Gitter%20B94-11.doc
http://www.bekphysik.de/Lk13/Loesungen/Quanten/Bragg%20De%20Broglie%20Doppels
palt%20%20Gitter-L%f6sung%20B94-11.doc
Ph 12
Photonenimpuls
Musteraufgaben
Leistungskursabitur Bayern 1998 Teilaufgabe III/1
Eine Platte der Fläche A = 4,0 cm2 wird von einer praktisch punktförmigen Lichtquelle
bestrahlt, die Licht der Wellenlänge  = 5,9 · 10–7 m emittiert und die sich im Abstand a
= 1,0 m vor der Platte befindet. Die isotrop in den Raum abgestrahlte Leistung beträgt P
= 20 W. Es darf angenommen werden, dass die Lichtstrahlen senkrecht auf die Platte
auftreffen, wobei 80 % der auftreffenden Strahlung reflektiert und 20 % absorbiert
werden.
a) Wie viele Photonen treffen pro Sekunde auf die Platte? [zur Kontrolle: n = 1,9 · 1015]
(6BE)
b) Wie groß ist die vom Licht auf die Platte ausgeübte Kraft? (6BE)
c) Begründen Sie ohne erneute Rechnung, in welchem Maße sich die ausgeübte Kraft
ändert, wenn das Absorptionsverhalten der Platte und die Leistung der Lichtquelle
gleich bleiben, aber
α) der Abstand a von 1,0 m auf 3,0 m erhöht wird bzw
ß) die Wellenlänge des verwendeten Lichts halbiert wird. (5 BE)
Ph 12
Photonenimpuls - Lösung
Musteraufgaben
Leistungskursabitur Bayern 1998 Teilaufgabe III/1
a)
und
=>
=>
b) Es gilt Kraftstoß gleich Impulsänderung. Die absorbierten 20% erfahren eine
Impulsänderung von pPhoton, die reflektierten 80% eine doppelt so große
Impulsänderung.
=>
c) α)
Bei Erhöhung des Abstands auf das dreifache, sinkt die Strahlungsleistung auf die
Platte auf ein neuntel, es sind also bei sonst gleichen Bedingungen nur der neunte
Teil an Photonen. Deshalb sinkt auch die Kraft auf ein neuntel der in b)
berechneten Kraft.
ß) Da bei Halbierung der Wellenlänge, sich der Impuls der einzelnen Photonen
verdoppelt aber die Anzahl der Photonen sich wegen der gleichbleibenden
Strahlungsleistung halbiert, ändert sich an der Kraft nichts.
Bohr
http://www.bekphysik.de/Lk13/Aufgaben/Quanten/Wasserstoff%e4hnlicheAtome.doc
http://www.bekphysik.de/Lk13/Loesungen/Quanten/L%f6sungWasserstoff%e4hnlicheAtom
e.doc
Ph 12
Spaltabstand am Doppelspalt
Musteraufgaben
Nach Gk-Abitur Bayern 2005 - 2 - 2
Bei einem Doppelspalt für optische Versuche ist die Beschriftung nicht mehr erkennbar.
Der Spaltabstand b soll nun experimentell mit Hilfe eines Lasers (Herstellerangabe:
) durch einen Schüler ermittelt werden. Der Abstand l zwischen
Schirm und Doppelspalt kann auf einer optischen Bank sehr genau eingestellt werden
und ist
. Der Schüler kann am Schirm auf beiden Seiten des 0.
Maximums jeweils 4 weitere Maxima beobachten. Den Abstand d der beiden äußersten
Maxima zueinander misst er zu
.
a) Skizzieren Sie den Versuchsaufbau mit den relevanten geometrischen Größen und
zeigen Sie unter Verwendung der Kleinwinkelnäherung, dass die Beziehung
zur Berechnung des Spaltabstandes gilt. (8 BE)
b) Berechnen Sie den kleinstmöglichen Wert sowie den größtmöglichen Wert für den
Spaltabstand. (4 BE)
Der Schüler bildet aus den Werten von Teilaufgabe 2b den Mittelwert für den
Spaltabstand und will den Doppelspalt mit dem Wert 331,5 μm beschriften.
c) Begründen Sie, warum diese Aufschrift eine falsche Genauigkeit vortäuschen würde.
(3 BE)
Ph 12
Musteraufgaben
Spaltabstand am Doppelspalt Lösung
Nach Gk-Abitur Bayern 2005 - 2 - 2
a)
Für den Gangunterschied beim 4. Maximum gilt:
Außerdem gilt:
Bei der Kleinwinkelnäherung kann
gesetzt werden, so dass gilt:
Da d4 = d/2 ist, gilt:
b) Berechnung des kleinstmöglichen Wertes für b:
Berechnung des größstmöglichen Wertes für b:
c) Die Unsicherheit in der Spaltbreite beträgt ca. 13μm. Die Angabe 331,5μm bedeutet
eine Genauigkeit von etwa 1/10 μm, was eine viel zu hohe Genauigkeit vortäuscht.
Ph 12
Musteraufgaben
Wellenaspekt
elektromagnetischer Strahlung
Nach LK-Abitur Bayern 1991-III-1
Mit der skizzierten Anordnung kann vom sichtbaren Licht der Kohlebogenlampe
(Wellenlängenbereich: 400nm bis 750nm) auf dem Schirm ein Gitterspektrum entworfen
werden.
a) Erklären Sie die Funktion von Kondensor, Spalt und Linse. (6 BE)
b) Wie breit ist das Gitterspektrum 1. Ordnung auf dem Schirm, wenn das Gitter 5000
Striche pro Zentimeter besitzt? (7 BE)
c) Prüfen Sie rechnerisch, ob es zu einer Überlappung der Gitterspektren 1. und 2.
Ordnung kommt. (7 BE)
d) Bis zu welcher maximalen Ordnung können Spektren vollständig beobachtet werden?
(6 BE)
e) Die Kohlebogenlampe werde nun durch eine Natriumdampflampe ersetzt. Welchen
Durchmesser muss die Blende mindestens haben, damit die benachbarten Natrium-DLinien (1=589,0nm und 2=589,6nm) in der 1. Ordnung getrennt werden können?
(7 BE)
h 12
Musteraufgaben
Wellenaspekt
elektromagnetischer Strahlung Lösung
Nach LK-Abitur Bayern 1991-III-1
a)

Der Kondensor dient zur optimalen Ausleuchtung des Spaltes.

Der Spalt (besser: Kohärenzspalt) stellt eine eng begrenzte Lichtquelle dar, bei
der die unkoordiniert emittierenden Lichtsender trotzdem noch eine
einigermaßen scharfe Interferenzfigur erzeugen.

Die Linse erzeugt von dem divergenten Lichtbündel, welches vom Spalt ausgeht,
ein Parallelbündel.
b)
Für konstruktive Interferenz am Gitter gilt:
Ordnung gilt:
. Für die 1.
Die Breite des Spektrums 1. Ordnung ist 10cm.
c) Größter Winkel des Spektrums 1. Ordnung:
Kleinster Winkel des Spektrums 1. Ordnung:
Da 2λblau > λrot ist auch sinα2,blau > sinα1,rot. Somit überlappen sich die Spektren 1. und
2. Ordnung nicht.
d) Zur größten Entfernung von der optischen Achse kommt es stets beim roten Licht. Man
muss nun prüfen, wie viele rote Maxima es in der Halbebene nach dem Gitter geben
kann (α k,rot  90°).
Für die Abschätzung nutzt man aus, dass der Sinus eines Winkels stets kleiner oder
gleich 1 sein muss:
Man kann also bei der Anordnung die 2. Ordnung des Spektrums vollständig
beobachten.
e) Eine Auflösung der Linien ist möglich, wenn:
Dabei bedeutet N die Zahl der beleuchteten Spalte. Da die Trennung in der 1. Ordnung
möglich sein soll:
Somit ergibt sich für den Durchmesser D der Blende:
D  N d  D  982 0,2 10-5m = 0,20cm
Der Blendendurchmesser muss größer als 2 mm sein