Heptagonreport

Heptagonreport
-1-
HEPTAGONREPORT von Alfred Rossi
NÄHERUNGSKONSTRUKTIONEN (S.1 – 5)
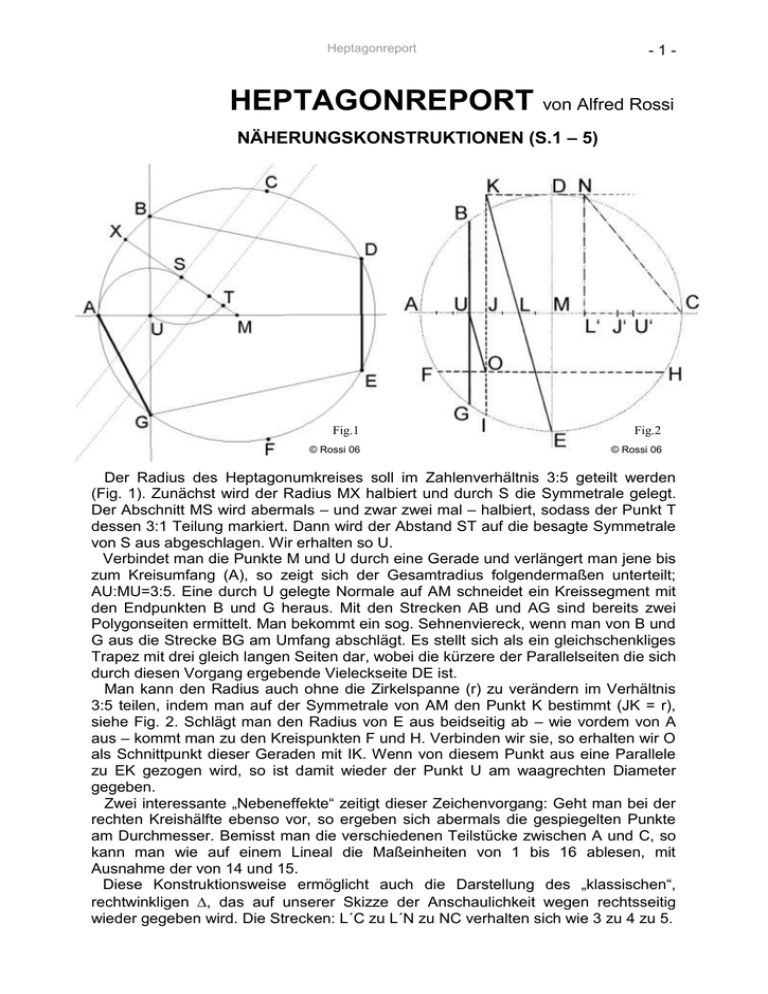
Fig.1
Fig.2
© Rossi 06
© Rossi 06
Der Radius des Heptagonumkreises soll im Zahlenverhältnis 3:5 geteilt werden
(Fig. 1). Zunächst wird der Radius MX halbiert und durch S die Symmetrale gelegt.
Der Abschnitt MS wird abermals – und zwar zwei mal – halbiert, sodass der Punkt T
dessen 3:1 Teilung markiert. Dann wird der Abstand ST auf die besagte Symmetrale
von S aus abgeschlagen. Wir erhalten so U.
Verbindet man die Punkte M und U durch eine Gerade und verlängert man jene bis
zum Kreisumfang (A), so zeigt sich der Gesamtradius folgendermaßen unterteilt;
AU:MU=3:5. Eine durch U gelegte Normale auf AM schneidet ein Kreissegment mit
den Endpunkten B und G heraus. Mit den Strecken AB und AG sind bereits zwei
Polygonseiten ermittelt. Man bekommt ein sog. Sehnenviereck, wenn man von B und
G aus die Strecke BG am Umfang abschlägt. Es stellt sich als ein gleichschenkliges
Trapez mit drei gleich langen Seiten dar, wobei die kürzere der Parallelseiten die sich
durch diesen Vorgang ergebende Vieleckseite DE ist.
Man kann den Radius auch ohne die Zirkelspanne (r) zu verändern im Verhältnis
3:5 teilen, indem man auf der Symmetrale von AM den Punkt K bestimmt (JK = r),
siehe Fig. 2. Schlägt man den Radius von E aus beidseitig ab – wie vordem von A
aus – kommt man zu den Kreispunkten F und H. Verbinden wir sie, so erhalten wir O
als Schnittpunkt dieser Geraden mit IK. Wenn von diesem Punkt aus eine Parallele
zu EK gezogen wird, so ist damit wieder der Punkt U am waagrechten Diameter
gegeben.
Zwei interessante „Nebeneffekte“ zeitigt dieser Zeichenvorgang: Geht man bei der
rechten Kreishälfte ebenso vor, so ergeben sich abermals die gespiegelten Punkte
am Durchmesser. Bemisst man die verschiedenen Teilstücke zwischen A und C, so
kann man wie auf einem Lineal die Maßeinheiten von 1 bis 16 ablesen, mit
Ausnahme der von 14 und 15.
Diese Konstruktionsweise ermöglicht auch die Darstellung des „klassischen“,
rechtwinkligen , das auf unserer Skizze der Anschaulichkeit wegen rechtsseitig
wieder gegeben wird. Die Strecken: L´C zu L´N zu NC verhalten sich wie 3 zu 4 zu 5.
Heptagonreport
-2-
Man kann nämlich mit diesen Maßen die
geometrische Deutung des Satzes von Pythagoras
(über das rechtwinklige ∆, d.h.: a² + b² = c²) durch die
ganzen Zahlen der Seiten – nämlich 3, 4 und 5 – sehr
augenfällig machen.
Wollte man ausschließlich dieses Zahlenverhältnis
darstellen, so hat man die Gerade FH beidseits
gleichmäßig zu verlängern, bis sie AC gleich kommt.
Dann hat man die Strecke DK so weit nach links zu
ziehen, sodass ein auf sie gefälltes Lot den Kreispunkt
© Rossi 06
A tangiert. Dieser Schnittpunkt (Q) und die Endpunkte
der elongierten Strecke FH bilden ein rechtwinkliges Dreieck mit eben diesem
Zahlenverhältnis (siehe Fig.2 der Vorseite und nebenstehende Skizze).
In der unten stehenden Grafik scheint die obige Skizze wieder auf, doch mit
einigen zusätzlichen Einzeichnungen, wie die Punkte F und S auf der Strecke A´C´.
Würde man die Kreispunkte F, H und D zu einem Dreieck verbinden, so hätte man
das ebenfalls in einem Kreis eingeschriebene große Dreieck der Abb. von S. 4 vor
sich. Dessen halbierte Seitenkante s/2, die wir hier mit FS bezeichnen, wurde dort
vom Basiswinkel aus, nach oben und unten abgeschlagen, wodurch sich die ersten
drei Heptagoneckpunkte am Umkreis ergaben.
© Rossi 06
Darauf verzichten wir jetzt, doch
wollen wir aus Vergleichsgründen FS auf
die Hypotenuse übertragen (siehe F´S´).
Deshalb werden zwei Kreisbögen, je von
C´ aus, nach oben gezogen – einmal mit
der Zirkelspanne des Radius und dann
mit der erweiterten von C´F. Die Bögen
schneiden die Gerade QH in T und V.
Diese Teilstrecke muss logischerweise
(etwas) länger als F´S´ sein und so einen
besseren
Näherungswert
für
die
Polygonseite s/2 bzw. FS abgeben. Als
Siebeneckseite genommen, ist s/2 um
0,210754%, der Abstand TV jedoch nur
um 0,0126% zu kurz.
In der unten stehenden Tabelle werden die Werte der Konstruktion von S. 1
angeführt (RO/1). Umseitig sind die Lösungen dieser Seite (RO/2), die von S. 4 oben
(IND/4) und eine zeitgenössische aus dem Internet (HU/5), die mit einem Raster
arbeitet,1 mit zunehmendem Grad der Abweichung gereiht.
(RO/1):
Wahre Polygonseite
100%
Polygonseite DE
101,202% (+1,202%)
Restliche Polygonseiten jeweils
99,799% (-0,201%)
Siehe: „www.geocities.com/robinhuiscool/heptagon.html“. Diese letzte der insgesamt fünf
Konstruktionen wurde herausgegriffen, da sie mit der vierten die beste und leicht zu zeichnen ist.
1
Heptagonreport
Korrekte
Daten
Siebeneck
Polygonseite
s[%]
Zentriwinkel

100
51,4286
-3-
RO/2
HU/5
IND/4
99,9874
100,0578
99,7992
51,4222
51,4605
51,3178
HISTORISCHES ZUM SIEBENECK
Im „liber de triangulis Jordani“, einem mittelalterlichen Werk über die Geometrie, das
vermutlich um die Mitte des 13. Jh. entstanden ist, wird am Ende des 23. Satzes des vierten
Buches (IV. 23) auf eine rechnerische Methode eingegangen, mit der sich die
Polygonseitenlänge eines jedweden Vielecks ermitteln lässt, während die zeichnerische
ausschließlich auf das Heptagon bezogen ist (zum Autor siehe Nonagonreport S. 15 f).
Beide Verfahren kämen aus Indien, versichert der anonyme Verfasser.1
Neben diesen beiden stellt Clagett noch drei weitere Lösungen vor. Sie alle sind nur mit
der sogenannten Bewegungsgeometrie zu meistern. Die erste macht den Hauptinhalt von
Proposition IV. 23 aus und geht auf ein arabisches Fragment zurück, das Gerard von
Cremona ins Lateinische übertrug [CL. S. 596ff].2 Die Abschrift dieses Lehrsatzes im „liber
de triangulis Jordani“ bringt Clagett auf den Seiten 418 – 422 (lat.) und 471ff (engl.). Sie wird
mit zwei anderen vom Autor in Beziehung gesetzt [Cl. 325 – 328, 473 6]. Diese beiden
anderen entstammen einem arabischen Werk, das den Titel trägt: „Über die Teilung eines
Kreises in sieben Teile.“ Sie existieren nur auf Arabisch, sollen aber auf Archimedes
zurückgehen. Allerdings findet man im heute noch existierenden Schrifttum der Antike keine
diesbezüglichen Lehrsätze [Cl. S. 325]. Sie wurden ins Deutsche übertragen von: C. SCHOY
„Die trigonometrischen Lehren des persischen Astronomen Abu ......al-Biruni“ (Hannover
1927), S. 82 – 84. Vom selben Autor ist zu empfehlen: „Graeco – Arabische Studien,“ Isis,
Bd. 8 (1926), S. 21 – 40. Siehe auch J.TROPFKE „Die Siebeneckabhandlungen des
Archimedes,“ Osiris, Bd. I (Berlin und Leipzig, 1937), S. 127 f [Cl. 325 18].
Als Ibn al-Haitham das Heptagon abhandelte, erwähnte er ebenfalls Archimedes (zum
Autor siehe S.16 im Nonagonreport). Überhaupt ist festzuhalten, dass dieses Problem unter
den arabischen Geometern sehr beliebt war [Cl. S. 326]. Literatur dazu: R. RASHED „La
construction de l´heptagone régulier par Ibn al-Haytham,“ IN Journal for the History of Arabic
Science, Bd. 3 (1979), S. 309 – 386 [Cl. S 326 19]. – Ein weiterer Aufsatz mit dieser
Fragestellung erschien von: A. ANBOUBA „Construction of the Regular Heptagon by Middle
Eastern Geometers of the Fourth Century,“ IN Journal for the History of Arabic Science, Bd.
1 (1977), S. 319, 384 [Cl. 326 20].
Siehe dazu CLAGETT, M. „Archimedes in the Middle Ages“, Bd. V (Philadelphia, 1984 / American
Philosophical Society for its Memoirs series, Volume 157), S. 422 f (lat. Text), 474 (engl. Text), S. 328.
KOMMENTAR: In der Fußnote 11 der S. 474 wird auf Hero von Alexandrien hingewiesen, der
möglicher Weise der Vater dieses Gedankens ist und ihn im 19. Kapitel seines 1. Buches „metrica“
festhielt. Clagett führt in dieser Fußnote die hiezu dienliche Literatur an: E. M. BRUINS „Codex
Constantinopolitanus Palatii veteris Nr. 1“, Teil II (Leiden, 1964), S.101 f. Er vermerkt hier weiters,
dass Hero einen zweiten Konstruktionsweg bringt. Es wird die Höhe eines Hexagonsektors als
Siebeneckseite genommen. Sie entspricht der halbierten Dreiecksseite, vorausgesetzt, dass das
Sechseck und das gleichseitige Dreieck dem gleichen Kreis eingeschrieben werden (siehe die Skizze
auf der nächsten Seite). Dieses alternative Verfahren scheint auch in der „Geometria deutsch“ von
Roriczer auf. Siehe L. R. SHELBY (Carbondale and Edwardsville, III., 1977) “Gothic Design
Techniques: The Fifteenth – Century Design Booklets of Mathes Roriczer and Hanns
Schmuttermayer”, S.118 f.
Anmerkung: Da die folgenden Verweise alle demselben Band Clagetts entstammen, werde ich sie den
betreffenden Sätzen als Klammerausdrücke anfügen. Das hieße für die Fußnote 11 der Seite 474 [Cl.
S. 447 11].
2 Gerard (Gherard) von Cremona (1114 - 1187) ging nach Toledo und erlernte dort zunächst das
Arabische. Mit einigen Mitarbeitern, wie man annimmt, übersetzte er an die 80 mathematische Werke
aus der graeco – arabischen Tradition.
1
Heptagonreport
-4-
INDISCHE METHODE
GEOMETRISCHE VARIANTE
Der Radius eines Kreises wird auf
seinem Umfang abgetragen. Indem man
nur jeden zweiten der so entstandenen
Punkte am Kreis durch eine Gerade
verbindet, entsteht ein gleichseitiges
Die nebenstehende Zeichnung macht
klar, dass dessen halbes Seitenmaß (s)
mit der Höhe (h) des Hexagonsektors
übereinstimmt.
Der Zentriwinkel eines Heptagonsektors beträgt 51,428571° (=360:7), bei dieser
Näherungskonstruktion bloß 51,3178°. Damit kommt man auf eine Polygonseite von
99,799246%.
ARITHMETISCHE VARIANTE
Clagett vereinfacht die im „liber de triangulis“ angeführte allgemeine Formel für das
Siebeneck und schreibt: s = ½ sqrt(3) r, wobei s die Heptagonseite und r der
Umkreisradius ist [Cl. S.328].1 Setzen wir für r 100 cm ein, ergeben sich für die
Polygonseite 86,6025 cm, während die wahre Länge 86,7767 cm beträgt. Dieses zu
geringe Maß entspricht 99,799246%, einem Wert, welcher der obigen
(geometrischen) Lösung überlegen ist, und dem zeichnerischen Ergebnis von S. 1
entspricht. Machen wir nun die Berechnung mit der allgemeinen Formel für das
Heptagon (r = 100 cm), so erhalten wir wieder und erwartungsgemäß – wie schon
oben – eine Siebeneckseite von 86,6025 cm. Diese für jedwedes regelmäßige
Vieleck geltende Formel lautet:
s² = (r.2r.9) / { [ n (n -1) / 2] + 3} oder s² = 18 r² / { [ n (n – 1) / 2] +3}.
Der Ausdruck n steht für die Eckenzahl, daher ist die Sieben einzusetzen.
Abu´l Wafa stellt in seinem „Buch der geometrischen Konstruktionen“ einige
Vieleckkonstruktionen u.a. auch die oben abgebildete vor. Er beschreibt sie kurz,
doch stellt er sie nicht dar, weist aber darauf hin, dass es sich um eine Approximation
handelt.2 In einem anderen Buch wandte er sich an Schreibkundige und Kaufleute,
um sie mit Grundkenntnissen der Arithmetik vertraut zu machen. Im dritten Band
dieses Werkes beschäftigte er sich mit den regelmäßigen Polygonen und stellt
folgende Formel auf;3 d² = s² [6 + n (n – 1)] / 9 bzw. die Umformung s² = 9d² / [6 +
n (n – 1)]. Nehmen wir die zweite Gleichung her und den Radius wieder mit 100
Einheiten an (d = Durchmesser). Wir erhalten für die Heptagonseite 86,60254
Einheiten bzw. 99,799246°, also ein Ergebnis wie bei der „Indischen Formel“. Wie
der Anonymus des “liber de triangulis“, bezeugt auch Abu´l Wafa den indischen
Ursprung dieser von ihm dargelegten Formel.
„sqrt(3)“ bedeutet Quadratwurzel aus 3 (square root). Da das V-förmige Wurzelzeichen
nicht verfügbar ist, werden im Folgenden quadratische Termini verwendet. Anstelle von s = ½
sqrt(3) r hieße das hier s² = ¾ r².
1
2
Zur Person siehe Nonagonreport S.14. Zu diesem Thema siehe dort Fußnote 3, die auf Suters
diesbezüglichen Aufsatz hinweist (S. 104).
3
Siehe R.C. GUPTA „Abu´l Wafa and his indian rule about regular polygons“ IN Bulletin of the Indian
Society for the history of Mathematics (Bd. 14, 1922, S. 57-61)
Heptagonreport
-5-
Abschließend wollen wir die beiden Formeln auch auf das Neuneck anwenden, da
der folgende Report von ihm handelt. Die abweichenden Werte der auf der Vorseite
behandelten Heptagonkonstruktion seien der Tabelle vorangestellt (das in der
Auflistung aufscheinende Zeichen steht für den Zentriwinkel des jeweiligen
Sektors).
r
s
s

[cm]
[cm]
[%]

r
s
s

Wahre Maße
des
HEPTAGONS
100
86,776748
100
51,428571
Wahre Maße des
NONAGONS
100
68,40403
100
40
INDISCHE FORMEL
HEPTAGON
NONAGON
[cm] 100
100
[cm] 86,60254038 67,9366221
[%] 99,79924641 99,3166953
°
51,31781255 39,7151372
Abweichende Werte der
SIEBENECK- KONSTRUKTION
100
86,6025404
99,7992464
51,3178126
ABU’L WAFAS FORMEL
HEPTAGON
NONAGON
100
100
86,60254038
61,2372436
99,79924641
89,5228594
51,31781255
35,6590877
Es fällt auf, dass beim Heptagon die geometrische und die zwei Wege der
algebraischen Lösung übereinstimmen. Beim Nonagon werden die Berechnungen
ungenauer, wobei Abu’l Wafas Ergebnis schlechter abschneidet.
Heptagonreport
-6-
KONSTRUKTION AUF KINEMATISCHER GRUNDLAGE
Die Kinematik beschäftigt sich mit der geometrischen Beschreibung von
Bewegungsabläufen.
Zu Beginn dieses historischen Abrisses wurde eine bewegungsgeometrische
Konstruktion angesprochen, auf die näher einzugehen Wert ist (siehe S. 3, 2.
Absatz). Um den korrekten Winkel zu ermitteln, bedarf es einer mechanischen
Apparatur.
Die entsprechende Textstelle des Gerhard
von Cremona [Cl. S. 597] und noch mehr das
darauf fußende Manuskript des „liber de
triangulis Jordani“ [Cl. S. 418 – 422] sind nicht
leicht zu verstehen. Vor allem der die
Bewegungsvorgänge betreffende Abschnitt
gibt zu missverständlichen Vorstellungen
Anlass; daher ist auch die englische Übersetzung [Cl. S. 471ff] oder wäre eine hier
angebotene Übertragung ins Deutsche nicht
hilfreich.
Clagetts eigene kurze Beschreibung von IV.
23 sei hier erwähnt [Cl. S. 327].
Bildanhang aus Curtzes Buch (siehe
Nonagonreport S. 15, Fußnote 3)
Ergo soll im Folgenden der 23. Lehrsatz des vierten Buches nicht übersetzt,
sondern dargelegt werden. Zum besseren Verständnis der „Hebelmaschinerie“ sind
vorab zwei Hilfszeichnungen dienlich.
Die Erste zeigt einen auf einer
Unterlage montierten Kreisring, seinen
senkrechten Durchmesser AB und das
Verbindungsstück QH. A und G werden
als Drehpunkte eingesetzt. Um den
Letzteren kreist der T- förmige Balken. In
seinem linken Endpunkt steckt ein Stift
(D), der naturgemäß diese Bewegung mit
vollzieht, was auch der zweite Stift, unten
am Umfang, in der Rille tut. Auch er kann
nur eine Kreisbahn beschreiben. In der
umseitigen Darstellung wird er weggelassen, da seine Funktion vom Stab
LM übernommen wird. Noch einen Dritten
gibt es. In der Nut zwischen Q und H
lässt sich der Stift selbstredend nur
geradlinig führen. An jedem von ihnen ist
der Kraftansatz möglich.
Heptagonreport
-7-
Die links stehende Abbildung
macht uns mit dem Mechanismus
des T-Balkens und der drei Stäbe
vertraut, deren Positionierung den
Beginn der Bewegungsphase markieren. Der am obersten Kreispunkt
festgemachte, schräg nach links
unten zeigende Stab AD würde, falls
er bewegt wird, wie ein Pendel hinund herschwingen. Der nach rechts
unten Gerichtete hingegen rotiert um
den Mittelpunkt (LM). Der Stift L
befindet sich auf LM und nicht am
Kreisring. Auf ihm drehbar fixiert ist
der Balken DL. L fungiert hiemit
während des Bewegungsvorgangs
als Angelpunkt beider Stäbe. Dabei
„wandert“ der linke Teil von DL immer mehr über den Kreis hinaus, unterschiedlich
zum Balken AD, der allmählich ins Kreisinnere „hineinwandert“. Alle Stäbe kreisen,
dank ihres Drehpunkts. Jenen besitzt DL
nicht und ist deshalb nirgendwo
ortsgebunden, vielmehr eignet ihm eine sich vom Mittelpunkt gesamtheitlich
entfernende Bewegung. Sie ist in einem geradlinig und rotierend. Man beachte: die
Punkte D und L kreisen am Ring.
Es versteht sich, dass das Bewegungsspiel erst durch die Langlöcher in den
Stäben ermöglicht wird. Wie sich dabei der beweglichen Elemente Richtungen und
Längen (innerhalb des Kreises) ändern, wollen wir zusammenfassen:
DG wahrt seine Länge / Bewegung gegen den Uhrzeigersinn
LM muss ebenfalls gleich lang bleiben / Bewegung im Uhrzeigersinn
AD wird länger / Bewegung gegen den Uhrzeigersinn
DL verkürzt sich, da es von den gegenläufigen Bewegungen der zwei Stäbe
gleichsam zusammen gedrückt wird / zieht, kaum seine Lage verändernd nach unten
(siehe Abb. auf S. 8 und vergleiche DL mit D´L´).
Wie sind nun die Rollen der Elemente in diesem Zusammenspiel verteilt? Das TStück und der Stab LM haben in G ihren Drehpunkt und in D bzw. L ihren
Angelpunkt. Hingegen zeigt der Stab AD seine „Eigenständigkeit“ nur im Drehpunkt
A. Er ist vom Angelpunkt D auf DG abhängig. Der Weg von DL wird durch den
Angelpunkt L auf LM und den Angelpunkt D auf DG bestimmt. Wir sehen, wie in der
hier genannten Reihenfolge die Glieder der Bewegungskette ihre „Eigenmächtigkeit“
verlieren.
Zur selben Wertigkeitsskala kommt man, wenn man den Bolzen auf QH
herausnimmt und einmal D nach unten drückt, das andere Mal L nach links schiebt.
Für DG (inklusive TY) und LM ändert sich punkto Bewegungsablauf und
Längenverhältnisse nichts. Bewegt man den einen Stab, bleibt logischer Weise der
andere in Ruhestellung – und umgekehrt. Doch sie ziehen AD und DL bzw. nur DL
mit, was deren größere Abhängigkeit im System beweist. AD beschreibt seine
gewohnte Bahn und wird länger, wenn es durch D (auf DG) abwärts gedrückt wird.
Heptagonreport
-8-
Für DL gilt aber: Es wird in Bewegung gesetzt, ob nun die Kraft und Richtung von D
oder L ausgeht, hat dabei aber jeweils eine andere Richtung. Doch beide haben mit
der ursprünglichen Bewegung (Abhängigkeit in E) nichts gemein.
Dieses „Experiment“ lässt andererseits auf die vorrangige Stellung von QH und
seinem beweglichen Griff rückschließen. Erst wenn die Stäbe AD und ML hier
„eingeschient“ werden, ergibt sich eine zielführende Gesamtbewegung.
Wenn man ein Modell baut, werden einem diese Zusammenhänge klarer. Um die
Maschinerie in Gang zu setzen, wählt man am besten den Griff in der Rille auf QH.
Nicht dafür anzuraten ist der Rundstab über L. Käme von dort der Kraftimpuls, so
würde wegen des spitzen Winkels zwischen QH und LM der Druck vom Angriffspunkt
auf die Rillenkante sehr stark sein und so die Schrägstellung des Bolzens
begünstigen, wodurch er Gefahr läuft sich zu verkeilen.
KONSTRUKTION: Wir betrachten zunächst die grau gezeichnete Figur, die wir schon
aus der vorhergehenden Abbildung kennen.
Man zeichne einen Kreis und
seine aufeinander normal stehenden Durchmesser. Vom Halbierungspunkt H des Radius AG aus
wird rechtwinklig eine Linie bis zum
Kreis gezogen (Q). Verbindet man
A mit D, dem Endpunkt des waagrechten Durchmessers, so schneiden sich die Strecken AD und QH in
E. Legt man durch E und G eine
Gerade, so berührt sie den Umfang
in M und L. Dann ist noch die Verbindungslinie von D nach L zu ziehen.
Nun wird das Lot auf den Radius
DG, vom Halbierungspunkt T beginnend, gefällt. Es sei angemerkt,
dass sich die Strecken AD und DG
nicht in T schneiden. Die Gerade TZ
geht über den Kreis hinaus, ihr
Ende sei unbestimmt. Sie schneidet
DL in K.
Mit der grauen Figur wird der Beginn, mit der schwarzen das Ende der Bewegung
angezeigt. Es ist erreicht, wenn der T´Z´ und D´L´ schneidende Punkt K´ auf AB liegt.
Die Sehne D´B entspricht der Heptagonseite.
Da wir es nicht mit einer Näherungskonstruktion zu tun haben, kann auch der
Beweis für die Richtigkeit erbracht werden.
Heptagonreport
-9-
BEWEIS DES KORREKTEN HEPTAGONWINKELS

I.
I.1 Zunächst soll bewiesen werden, dass der
D´GK´ doppelt so großwie derD´AG ist.
Letzterer sei α genannt.
I.2 Das ∆ GAE´ ist gleichschenklig, da
über dem Halbierungspunkt H die
Dreiecksspitze E´ liegt, daher
→
I.3 Auch das ∆ AD´G hat gleich lange
Schenkeln (jeweils Radiuslänge).
z. z.:D´GK´ = 2 D´AG = α
D´AG = E´AG = AGE´ = α
D´AG = AD´G = α
I.4 Ein gestreckter Winkel hat 180°, wie der AGK´.
Um den D´GK´ zu bestimmen, hat man den
Scheitelwinkel des ∆ AD´G von 180° abzuziehen.
180 –  AGD´ =  D´GK´
I. 5 Um den AGD´ zu erhalten, hat man
 AGD´ = 180 – ( AD´G +  D´AG)
die beiden Basiswinkel des ∆ AD´G von 180° abzu AGD´ = 180 – (α + α)
ziehen, da die Winkelsumme im Dreieck 180° beträgt.
 AGD´ = 180 – 2α
I.6 Da, wie weiter oben gesagt (I. 4), der  D´GK´ 180 –  AGD´ ist, hat man für
den A GD´ einzusetzen:
 D´GK´ = 180 – (180 – 2α) = 2α
......................................................................................................................................
Heptagonreport
- 10 -
II.
II.1 Nun wollen wir beweisen, dass
z.z.: E´GD´ = 2  D´GK´
der  E´GD´ doppelt so groß wie der
 D´GK´ = β
D´GK´ist. Wir bezeichnen jenen mit β.
II.2 Auch das ∆ D´L´G ist gleichschenklig
auf Grund der 2 gleich langen Schenkeln.
D´G = GL´ = r
 GD´L´=  GL´D´
II.3 Der Scheitelwinkel dieses ∆ ist demnach:  D´GL´ = 180 – ( GD´L´+  GL´D´)
II.4 Um den  E´GD´ zu ermitteln, hat man den Wert des Scheitelwinkels D´ GL von
180 abzuziehen
 E´GD´ = 180 – D´GL´
Wir setzen ein (siehe II.3):
 E´GD´ = 180 – [180 – ( GD´L´ +  GL´D´)]
II.5 Was ist nun für die Winkeln GD´L´ und GL´D´ einzusetzen? Betrachten wir
deshalb das ∆ D´K´G. Da die Höhe T´K´ die Basiskante D´G halbiert, müssen die
Winkeln GD´K´ (= GD´L´) und D´GK´ gleich groß sein (den  D´GK´ haben wir mit
ß bezeichnet).
II.6 Wir schreiben (siehe II.4): E´GD´ = 180 – [180 – (β + β)]
E´GD´ = 2β
----------------------------------------------------------------------------------------------------------------Die Winkeln im Halbkreis AD´B setzen sich wie folgt zusammen:
D´GB = β = 2α
D´GE´ = 2β = 4α
AGE´ = α = ½β
Summe
~ 1β
~ 2β
~½β
3½ β
Da: 3½β + 3½β = 7β, ist der  D´GB der korrekte Zentriwinkel (1/7), und die
Sehne D´B hat als Polygonseite die richtige Länge.