Bearbeiten - Ihre Homepage bei Arcor

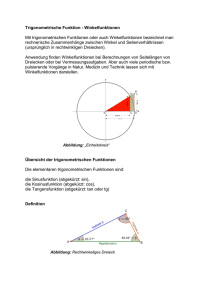
Herkunft des Namens [Bearbeiten]
Die Bezeichnung „Sinus“ leitet sich von dem lateinischen „sinus“ ab, was soviel heißt wie
„Bogen“ oder „Busen“. Das Wort ist mit „jiva“ aus dem Sanskrit verwandt, wo es etwa
„Bogensehne“ bedeutet. Im Arabischen entwickelte sich das Wort zu „jiba“: „Tasche“ oder
„Kleiderfalte“. Im Arabischen wird das Wort „jiba“ (‫ )بيج‬gleich geschrieben, wie „jaib“
(‫)بيج‬, was „Busen“ bedeutet.
Die Bezeichnung „Kosinus“ entwickelte sich aus complementi sinus, also Sinus des
Komplementärwinkels. Diese Bezeichnung wurde zuerst in den umfangreichen
trigonometrischen Tabellen verwendet, die von Georg von Peuerbach und seinem Schüler
Regiomontanus erstellt wurden [1].
Definitionen [Bearbeiten]
Definition am rechtwinkeligen Dreieck [Bearbeiten]
Dreieck mit einem rechten Winkel in C
In einem rechtwinkligen Dreieck gilt:
Der Sinus eines Winkels ist das Verhältnis der Gegenkathete (Kathete, die dem Winkel
gegenüberliegt) zur Hypotenuse (Seite gegenüber dem rechten Winkel).
Der Kosinus ist das Verhältnis der Ankathete (das ist jene Kathete, die einen Schenkel des
Winkels bildet) zur Hypotenuse.
Bei den für Dreiecke üblichen Bezeichnungen der Größen (Hypotenuse c) gilt hier:
und
Da aus geometrischen Gründen die Hypotenuse die längste Seite ist (denn sie liegt dem
größten Winkel, also dem rechten Winkel, gegenüber), gelten auch stets sin (α) ≤ 1 und cos
(α) ≤ 1.
Betrachtet man statt α den gegenüberliegenden Winkel β, so wechseln beide Katheten ihre
Rolle, die Ankathete von α ist die Gegenkathete von β und die Gegenkathete von α ist die
Ankathete von β, es gilt also
und
Da im rechtwinkeligen Dreieck
gilt, folgt
und
.
Auf dieser Beziehung beruht auch die Bezeichnung Kosinus, nämlich der Sinus des
Komplementärwinkels.
Aus dem Satz des Pythagoras folgt die Beziehung
sin2(α) + cos2(α) = 1.
Im rechtwinkligen Dreieck lassen sich Sinus und Kosinus nur für Winkel zwischen 0 und 90
Grad definieren.
Für beliebige Winkel ist der Sinus als y-Koordinate und der Kosinus als x-Koordinate eines
Punktes am Einheitskreis (s.u.) definiert.
Mittels Potenzreihendarstellung lässt sich die Definition auf komplexe Argumente
verallgemeinern.
Definition mit Einheitskreis [Bearbeiten]
Einheitskreis
Da im rechtwinkeligen Dreieck der Winkel zwischen Hypotenuse und Kathete Werte von 0
bis 90 Grad annehmen kann, sind Sinus und Kosinus zunächst nur für solche Winkel definiert.
Für eine allgemeine Definition betrachtet man einen Punkt P mit den Koordinaten (x,y) auf
dem Einheitskreis, also x2 + y2 = 1. Der Ortsvektor von P schließt mit der x-Achse einen
Winkel α ein. Der Koordinatenursprung (0,0), der Punkt (x,0) auf der x-Achse und der Punkt
P(x,y) bilden ein rechtwinkliges Dreieck. Die Länge der Hypotenuse beträgt
. Die Ankathete des Winkels α ist der Vektor (x,0) der Länge x, es gilt also
Die Gegenkathete des Winkels α ist der Vektor von (x,0) nach (x,y), also der Vektor (0,y) der
Länge y, es gilt also
Die y-Koordinate eines Punktes im ersten Quadranten des Einheitskreises entspricht also dem
Sinus des Winkels zwischen seinem Ortsvektor und der x-Achse, die x-Koordinate dem
Kosinus des Winkels. Setzt man diese Definition in den anderen Quadranten fort, so lassen
sich Sinus und Kosinus für beliebige Winkel definieren.
Für negative Winkel betrachte man die Beziehung
und
,
aus der sich Sinus und Cosinus für den vierten Quadranten, also Winkel zwischen -90 und 0
Grad berechnen lassen. Der Sinus ist also eine ungerade Funktion, der Kosinus eine gerade.
Für Winkel größer 90 Grad betrachte man die Beziehung
und
,
aus der sich Sinus und Cosinus für den zweiten und dritten Quadranten, also Winkel zwischen
90 und 270 Grad berechnen lassen.
Für Winkel kleiner -90 Grad und größer 270 Grad ergeben sich Sinus und Kosinus aus den
Beziehungen
und
;
Sinus und Kosinus sind also periodische Funktionen mit Periode 360 Grad.
Graph der Sinusfunktion
Graph der Kosinusfunktion
Wertebereich und spezielle Funktionswerte [Bearbeiten]
Zusammenhang zwischen Sinus und Kosinus [Bearbeiten]
(Satz des Pythagoras)
Insbesondere folgt daraus
und
. Diese Ungleichung gilt aber nur
für reelle Argumente α; für die über die Potenzreihe definierten komplexen Argumente
können Sinus und Kosinus beliebige Werte annehmen.
Verlauf des Sinus in den vier Quadranten [Bearbeiten]
In den vier Quadranten ist der Verlauf der Sinusfunktion folgendermaßen:
Quadran
t
Bogenma Bildmeng Monotoni Konvexitä
Punkttyp
ß
e
e
t
Gradmaß
0
Nullstelle,
Wendepunk
t
0
0 < x < π / positiv: 0
steigend
2
< sinx < 1
1.
Quadrant
π/2
1
Maximum
π / 2 < x < positiv: 0
fallend
π
< sinx < 1
2.
Quadrant
π
4.
Quadrant
konkav
Nullstelle,
Wendepunk
t
0
negativ: −
π < x < 3π
1 < sinx < fallend
/2
0
3.
Quadrant
konkav
3π / 2
−1
3π / 2 < x
< 2π
negativ: −
1 < sinx < steigend
0
konvex
Minimum
konvex
Für Argumente außerhalb dieses Bereiches erhält man den Wert des Sinus daraus, dass der
Sinus periodisch mit der Periode 360° (bzw. 2π rad) ist, d. h.
Außerdem gilt
.
Verlauf des Kosinus in den vier Quadranten [Bearbeiten]
Der Kosinus ist ein um 90° (bzw. π/2 rad) phasenverschobener Sinus, es gilt
.
.
In den vier Quadranten ist der Verlauf der Kosinusfunktion daher folgendermaßen:
Quadran
t
Gradmaß
Bogenma Bildmeng Monotoni Konvexitä
Punkttyp
ß
e
e
t
0
1.
Quadrant
0 < x < π / positiv: 0
fallend
2
< cosx < 1
π/2
2.
Quadrant
4.
Quadrant
Maximum
konkav
Nullstelle,
Wendepunk
t
0
negativ: −
π/2<x<
1 < cosx < fallend
π
0
π
3.
Quadrant
1
konvex
−1
negativ: −
π < x < 3π
1 < cosx < steigend
/2
0
3π / 2
0
3π / 2 < x
< 2π
positiv: 0
steigend
< cosx < 1
Minimum
konvex
Nullstelle,
Wendepunk
t
konkav
Für Argumente außerhalb dieses Bereiches erhält man den Wert des Kosinus daraus, dass der
Kosinus so wie der Sinus periodisch mit der Periode 360° (bzw. 2π rad) ist, d. h.
. Außerdem gilt
Wichtige Funktionswerte [Bearbeiten]
.
Winkel α
0π
π
Sinus
Kosinus
nicht definiert
Tangens
nicht definiert
Weitere mit Quadratwurzeln angebbare Funktionswerte [Bearbeiten]
Über die Berechnung der fünften Einheitswurzeln mittels einer quadratischen Gleichung
erhält man
Mit Hilfe der Additionstheoreme kann man viele weitere solche Ausdrücke berechnen:
erhält man aus
.
Aus
und
,
lassen sich dann z. B.
und dann rekursiv auch alle
berechnen.
Generell gilt, dass
und
zumindest dann explizit mit den Grundrechenarten und
Quadratwurzeln darstellbar sind, wenn der Winkel mit Zirkel und Lineal konstruierbar ist,
insbesondere also wenn
und die
für
ist
von der Gestalt
ist, wobei
,
Fermatsche Primzahlen sind [2]. In obigem Beispiel von
und der Nenner gleich
Umkehrfunktion [Bearbeiten]
Da sich zu einem gegebenen Wert
vierten Quadranten und zu einem gegebenen Wert
ein passender Winkel im ersten oder
ein passender Winkel
im ersten oder zweiten Quadranten konstruieren lässt, folgt aus diesen geometrischen
Überlegungen, dass die Funktionen
und
eine Umkehrfunktion besitzen. Diese Umkehrfunktionen
bzw.
werden Arkusfunktionen genannt. Der Name rührt daher, dass sich deren Wert nicht nur als
Winkel, sondern auch als Länge eines Kreisbogens (Arcus bedeutet Bogen) interpretieren
lässt; für diese Interpretation ist die Angabe des Wertebereichs im Bogenmaß
bzw.
üblich. Eine andere Interpretation des Wertes als doppelter Flächeninhalt des dazugehörigen
Kreissektors am Einheitskreis ist ebenfalls möglich; diese Interpretation ist insbesondere für
die Analgoie zwischen Kreis- und Hyperbelfunktionen nützlich.
Für die Arkusfunktionen gelten unter anderem folgende Formeln:
, denn für
gilt
, denn für
gilt
.
und
.
, denn für
und
gilt
.
, denn für
und
Stetigkeit [Bearbeiten]
Da die Sinusfunktion
gilt
.
und
und die Kosinusfunktion
monoton, surjektiv und invertierbar sind, folgt, dass sie in diesen Quadranten stetig sind. Da
die Funktionen in den anderen Quadranten lediglich gespiegelt bzw. periodisch fortgesetzt
sind, sind die Sinus- und Kosinusfunktion für alle reellen Argumente stetig.
Zusammenhang mit dem Skalarprodukt [Bearbeiten]
Der Kosinus steht in enger Beziehung mit dem Skalarprodukt zweier Vektoren
und
:
,
das Skalarprodukt ist also die Länge der Vektoren multipliziert mit dem Kosinus des
eingeschlossenen Winkels. In endlichdimensionalen Räumen lässt sich diese Beziehung aus
dem Kosinussatz ableiten. In abstrakten Vektorräumen mit innerem Produkt wird über diese
Beziehung der Winkel zwischen Vektoren definiert.
Additionstheoreme [Bearbeiten]
Aus dem Skalarprodukt lassen sich die sogenannten Additionstheoreme herleiten:
Die Vektoren
und
Winkel α − β ein; mit dem Skalarprodukt folgt also
der Länge 1 schließen den
.
Die Vektoren
und
den Winkel α + β ein; mit dem Skalarprodukt folgt also
der Länge 1 schließen
.
Aus
und
erhält man die Additionstheoreme für den Sinus:
sowie
.
Setzt man in diesen Beziehungen u = α + β und v = α − β (beziehungsweise
und
), so erhält man durch Addition bzw. Subtraktion je zweier
Additionstheoreme
,
,
und
.
Weitere Identitäten finden sich in der Formelsammlung Trigonometrie.
Ableitung (Differentiation) und Integration von Sinus und
Kosinus [Bearbeiten]
Differentiation [Bearbeiten]
Wird im Bogenmaß angegeben, so gilt für die Ableitung der Sinusfunktion [3]
Aus
und der Kettenregel erhält man die Ableitung des Kosinus:
und daraus die zweite Ableitung des Sinus:
.
Die dritte Ableitung ist daher
.
und die vierte Ableitung ist wieder die Sinusfunktion selbst:
.
In weiterer Folge erhält man daraus für die 4n + k-te Ableitung des Sinus
und für die 4n + k-te Ableitung des Kosinus
Wird der Winkel α in Grad gemessen, so kommt nach der Kettenregel bei jeder Ableitung ein
Faktor
dazu, also beispielsweise
. Um diese störenden
Faktoren zu vermeiden, wird in der Analysis der Winkel ausschließlich im Bogenmaß
angegeben; die Angabe von Winkel in Grad ist allerdings anschaulicher und daher bei
geometrischen Überlegungen zweckmäßiger.
Das Integral von Sinus und Cosinus lässt sich leicht mit der folgenden Skizze merken:
+Sinus
-Cosinus
+Cosinus
-Sinus
Man schreibt den +Sinus oben auf ein Blatt Papier und ergänzt auf der gegenüberliegenden
Seite -Sinus; man schreibt den +Cosinus rechts auf das Blatt Papier und ergänzt auf der
gegenüberliegenden Seite -Cosinus.
Liest man mit dem Uhrzeigersinn, kommt man bei der jeweiligen Ableitung aus; liest man
gegen den Uhrzeigersinn, kommt man beim jeweiligen Integral aus.
So entspricht z. B. die Ableitung von -Sinus dem -Cosinus. So entspricht z. B. das Integral
des -Sinus dem +Cosinus.
Integration [Bearbeiten]
Aus den Ergebnissen über die Ableitung ergibt sich unmittelbar die Stammfunktion von Sinus
und Kosinus im Bogenmaß:
Analytische Definition [Bearbeiten]
Obige Definitionen des Sinus und des Kosinus beinhalten geometrische Überlegungen.
Geometrie wird häufig naiv-intuitiv und nicht auf axiomatischer Basis behandelt. Sinus und
Kosinus spielen aber auch eine wichtige Rolle in der Analysis, in der ein viel formalerer
Zugang zweckmäßig ist. Daher sind die geometrischen Definitionen für die Analysis nicht
ausreichend, und es wird eine analytische Definition benötigt. Auf Basis einer streng
formalisierten Geometrie lässt sich zwar die Äquivalenz der geometrischen und der
analytischen Definition zeigen; auf Basis einer naiven Geometrie sind die geometrischen
Überlegungen allerdings lediglich als Heuristik zur Begründung der analytischen Definition
zu betrachten.
Die analytische Definition erlaubt zusätzlich die Erweiterung auf komplexe Argumente. Sinus
und Kosinus als komplexwertige Funktion aufgefasst sind holomorph und surjektiv.
Für die analytische Definition gibt es in der Literatur keinen einheitlichen Zugang; es sind
mehrere äquivalente Varianten verbreitet. In jeder dieser Varianten ist der Winkel im
Bogenmaß; bei Angabe des Winkels in Grad würden störende Faktoren dazukommen.
Definition als Taylorreihe [Bearbeiten]
Mit Hilfe der aus geometrischen Überlegungen berechneten Ableitung des Sinus gilt für die
4n + k-te Ableitung an der Stelle 0
Daraus ergibt sich folgende Taylorreihenentwicklung um x=0:
Für die aus geometrischen Überlegungen berechneten Ableitung des Kosinus gilt für die 4n +
k-te Ableitung an der Stelle 0
Daraus ergibt sich folgende Taylorreihenentwicklung um x=0:
Mit dem Quotientenkriterium lässt sich zeigen, dass diese Potenzreihen für jede komplexe
Zahl x absolut und in jeder beschränkten Teilmenge der komplexen Zahlen gleichmäßig
konvergieren. Diese unendlichen Reihen verallgemeinern also die Definition des Sinus und
des Kosinus von reellen auf komplexe Argumente. In der Analysis werden die Sinusfunktion
und die Kosinusfunktion häufig mittels dieser Reihenentwicklung definiert. Auch π wird dort
üblicherweise nicht geometrisch, sondern beispielsweise über diese Reihe und die Beziehung
als das Doppelte der kleinsten positiven Nullstelle der Kosinusfunktion
definiert.
Für kleine Werte zeigen diese Reihen ein sehr gutes Konvergenzverhalten. Zur numerischen
Berechnung kann man daher die Periodizität und Symmetrie der Funktionen ausnutzen und
den x-Wert bis auf den Bereich -π/4 bis π/4 reduzieren (siehe Reduktionsformel). Danach sind
für eine geforderte Genauigkeit nur noch wenige Glieder der Reihe zu berechnen. Das
Taylorpolynom der Kosinusfunktion bis zur vierten Potenz z.B. hat im Intervall [-π/4, π/4]
einen relativen Fehler von unter 0,05%. Im Artikel Taylor-Formel sind einige dieser so
genannten Taylorpolynome grafisch dargestellt und eine Näherungsformel mit
Genauigkeitsangabe angegeben. Zu beachten ist allerdings, dass die Teilsummen der
Taylorpolynome nicht die bestmögliche numerische Approximation darstellen; beispielsweise
in Abramowitz-Stegun finden sich Näherungspolynome mit noch kleinerem
Approximationsfehler.[4]
Beziehung zur Exponentialfunktion [Bearbeiten]
Die trigonometrischen Funktionen sind eng verbunden mit der Exponentialfunktion. Dieser
Ansatz führt zum einen Sinus und Kosinus auf nur eine Reihe zurück, und ist aus der
Eulerformel
.
motiviert. Für eine reelle Zahl
der komplexen Zahl
.
ist also
der Realteil und
Für beliebige komplexe Zahlen z definiert man dann
der Imaginärteil
und
Man kann aber auch den Sinus wie oben als Taylorreihe definieren und dann die
Übereinstimmung mit dieser Definition zeigen.
Ausgehend von dieser Definition lassen sich sehr leicht die Eigenschaften des Sinus und die
Additionstheoreme des Sinus und Kosinus nachweisen.
Definition über analytische Berechnung der Bogenlänge [Bearbeiten]
Die Definition des Sinus und Kosinus als Taylorreihe liefert keinen analytischen Beweis der
Differenzierbarkeit des Sinus und Kosinus, sondern setzt die Differenzierbarkeit letztlich
axiomatisch voraus. Die Definition mit Hilfe der Exponentialfunktion hat das selbe Problem,
versteckt es allerdings im Beweis der Eulerformel.
Ein echter analytischer Beweis der Differenzierbarkeit des Sinus und Kosinus erfordert, dass
die geometrische Definition des Sinus und Kosinus zuerst analytisch formalisiert wird. Dies
ist möglich, indem man den Einheitskreis
beispielsweise als
parametrisiert. Die Länge dieser Kurve wird auch als Bogenlänge bezeichnet und berechnet
sich als
Wie leicht zu zeigen ist, ist
ungerade, stetig, streng monoton wachsend und beschränkt.
Da die gesamte Bogenlänge dem Kreisumfang entspricht, folgt, dass das Supremum von
gleich
definiert.
ist;
wird bei dieser Vorgangsweise also analytisch als Supremum von
Die Funktion
ist auch differenzierbar:
.
Weil sie stetig und streng monoton wachsend ist, ist sie auch invertierbar, und für die
Umkehrfunktion
gilt
.
Mit Hilfe dieser Umkehrfunktion
lassen sich nun Sinus und Kosinus als - und Komponente von analytisch definieren:
sowie
.
Aus der Quotientenregel und der Kettenregel folgen dann
sowie
.
Bei dieser Definition des Sinus und Kosinus über die analytische Berechnung der Bogenlänge
werden die geometrischen Begriffe tatsächlich sauber formalisiert. Sie hat allerdings den
Nachteil, dass im didaktischen Aufbau der Analysis der Begriff der Bogenlänge erst sehr spät
formal eingeführt wird und daher Sinus und Kosinus erst relativ spät verwendet werden
können.
Definition als Lösung einer Funktionalgleichung [Bearbeiten]
Eine anderer analytischer Zugang ist, Sinus und Kosinus als Lösung einer
Funktionalgleichung zu definieren, die im Wesentlichen aus den Additionstheoremen besteht:
Gesucht ist ein Paar stetiger Funktionen
Gleichungen
, das für alle
die
und
erfüllt. Die Lösung definiert dann den Sinus, die Lösung den Kosinus. Um Eindeutigkeit
zu erreichen, sind einige Zusatzbedingungen zu erfüllen. In Heuser, Lehrbuch der Analysis,
Teil 1 wird zusätzlich gefordert, dass
eine ungerade Funktion,
eine gerade Funktion,
, und
gilt. Bei diesem Zugang wird offensichtlich die Differenzierbarkeit des Sinus vorausgesetzt;
wird in weiterer Folge analytisch als das doppelte der kleinsten positiven Nullstelle des
Kosinus definiert. Verwendet man den Zugang von Leopold Vietoris[5] und berechnet die
Ableitung des Sinus aus den Additionstheoremen, so ist es zweckmäßiger, auf geeignete
Weise analytisch (beispielsweise als Hälfte des Grenzwerts des Umfangs des dem
Einheitskreis engeschriebenen
-Ecks) zu definieren und dann die Differenzierbarkeit der
Lösung dieser Funktionalgleichung zu beweisen. Als Zusatzbedingung zu den
Additionstheoremen fordert man dann beispielsweise
,
, und
für alle
.
Unter den getroffenen Voraussetzungen ist die Eindeutigkeit der Lösung der
Funktionalgleichung relativ einfach zu zeigen; die geometrisch definierten Funktionen Sinus
und Kosinus lösen auch offensichtlich die Funktionalgleichung. Die Existenz einer Lösung
lässt sich analytisch beispielsweise nachweisen, indem man zeigt, dass die Taylorreihen von
Sinus und Kosinus oder eine andere der oben verwendeten analytischen Darstellungen von
Sinus und Kosinus die Funktionalgleichung tatsächlich lösen.
Produktentwicklung [Bearbeiten]
ist dabei im Bogenmaß zu nehmen.
Anwendungen [Bearbeiten]
Geometrische Anwendungen [Bearbeiten]
Skizze zum Beispiel
Mit der Definition des Sinus können auch im nicht rechtwinkligen Dreieck Größen, speziell
die Höhen, berechnet werden; ein Beispiel ist die Berechnung von hc im Dreieck DBC bei
gegebener Länge a und Winkel β:
Andere wichtige Anwendungen sind der Sinussatz und der Kosinussatz.
Fourierreihen [Bearbeiten]
Im Hilbertraum
der auf dem Intervall
bezüglich des Lebesgue-Maßes
quadratisch integrierbaren Funktionen bilden die Funktionen
ein vollständiges Orthogonalsystem, das sogenannte trigonometrische System. Daher lassen
sich alle Funktionen
als Fourierreihe
darstellen, wobei die Funktionenfolge
in der L2-Norm gegen
konvergiert.
Physikalische Anwendungen [Bearbeiten]
In der Physik werden Sinus- und Kosinusfunktion zur Beschreibung von Schwingungen
verwendet. Insbesondere lassen sich durch die oben erwähnten Fourierreihen beliebige
Signale als Summe von Sinus- und Kosinusfunktionen darstellen, siehe Fourieranalyse