STANDARDS zu Exponential- und Logarithmusfunktion

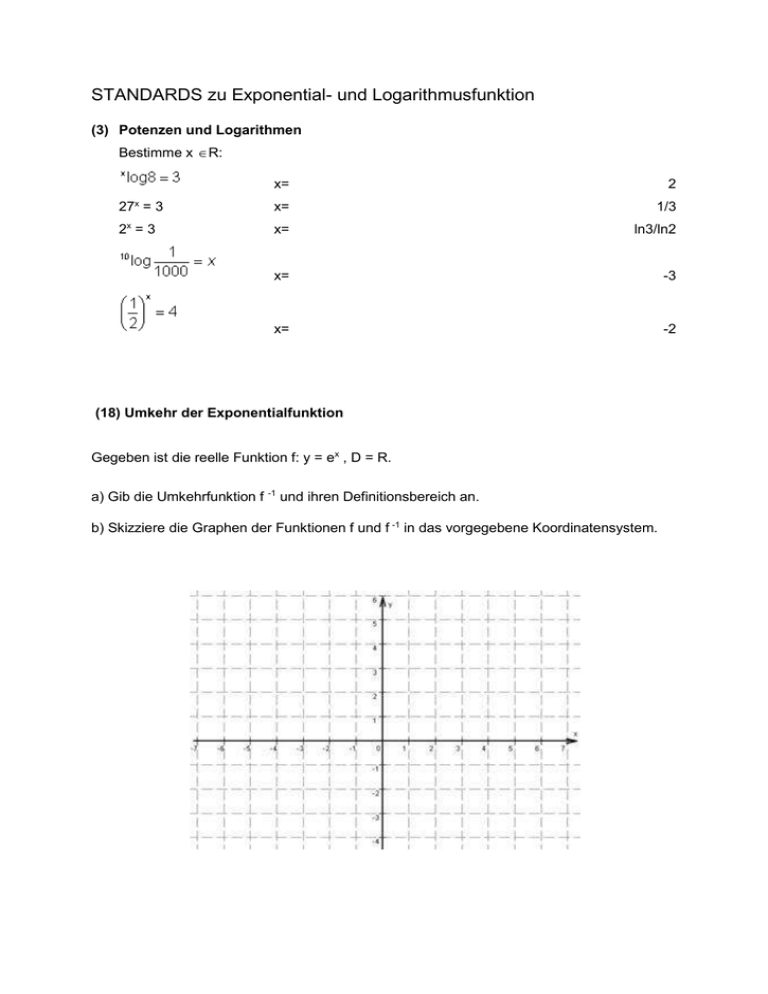
STANDARDS zu Exponential- und Logarithmusfunktion
(3) Potenzen und Logarithmen
Bestimme x  R:
x=
2
27x = 3
x=
1/3
2x = 3
x=
ln3/ln2
x=
-3
x=
-2
(18) Umkehr der Exponentialfunktion
Gegeben ist die reelle Funktion f: y = ex , D = R.
a) Gib die Umkehrfunktion f -1 und ihren Definitionsbereich an.
b) Skizziere die Graphen der Funktionen f und f -1 in das vorgegebene Koordinatensystem.
(21) Luftdruck
Der atmosphärische Luftdruck p(h) nimmt mit zunehmender Höhe h ab.
Es gilt das Gesetz
. p0: Luftdruck in Meereshöhe
p(h): Luftdruck in der Höhe h
k: Konstante
Der Luftdruck auf Meeresniveau (h = 0m) beträgt 1013 mbar, in 4000m Höhe nur
mehr 600 mbar.
a) Berechne den Luftdruck am Hochschwabgipfel (2277m).
852 mbar
b) In welcher Höhe beträgt der Luftdruck nur mehr die Hälfte des Drucks
verglichen mit in der Höhe h = 0m?
h = 5291 m
(22) Rekursives Modell
Gegeben ist das rekursive Funktionsmodell: N(t+1) = q.N(t)
a) Stelle die Funktionen für q=1,2 und q=0,8, sowie N(0)=1000 grafisch dar (Ausdruck oder
Skizze). Gib die dazugehörigen Wertetabellen im Intervall [0; 10] an.
b) Für welche Prozesse könnten solche Funktionen mathematische Modelle sein?
(26) Waldbestand
Der Holzbestand eines Waldes beträgt 7 000 m3. Ohne Schlägerung ist er in
10 Jahren auf ca. 9 000 m3 angewachsen.
Wie groß war der jährliche prozentuelle Zuwachs?
q = 1,0254499 … +2,5%
(29) Wachsen
Die Formel N(t) = N0 at mit a > 1 beschreibt ein exponentielles Wachstum.
Kreuze an, welche Aussagen richtig bzw. falsch sind.
richtig falsch
Die relative Zunahme ist in gleichen Zeitintervallen gleich groß.
Die absolute Zunahme ist in gleichen Zeitintervallen gleich groß.
Die relative Zunahme ist unabhängig von N0.
Die absolute Zunahme ist unabhängig von N0.
Die relative Zunahme ist abhängig von a.
Die absolute Zunahme ist abhängig von a.
(40) Medikamentenspiegel
Angenommen, innerhalb von 4 Stunden werden jeweils 25% eines Medikamentes vom
Körper abgebaut und ausgeschieden. Die wirksame Anfangsdosis beträgt 100 mg, alle
4 Stunden werden erneut 100 mg gegeben. Wie entwickelt sich im Lauf der Zeit der
Medikamentenspiegel im Körper?
a) Verwende eine rekursive Beschreibung des Sachverhaltes und stelle den zeitlichen
Verlauf des Medikamentenspiegels für die ersten zwanzig 4-Stunden-Intervalle grafisch
dar (es genügt, jeden zweiten oder dritten 4-Stunden-Intervallwert einzuzeichnen).
b) Mit welchem der folgenden vier Diagramme würde sich die Situation nach der
Stabilisierung des Medikamentenspiegels (also nach etwa 20 Intervallen) innerhalb
eines 4-Stunden-Intervalls am besten beschreiben lassen?
c) Ein Personenkreis diskutiert den zeitlichen Verlauf des Medikamentenspiegels im
Verlauf von mehreren aufeinanderfolgenden 4-Stunden-Intervallen.
Folgende Meinungen werden vertreten:
(i)
Im Lauf der Zeit steigt der Medikamentenspiegel ständig und gleichmäßig an.
(ii) Der Medikamentenspiegel bewegt sich zwischen zwei Werten hin und her, die
aber beide (nach einiger Zeit) konstant bleiben.
(iii) Der Medikamentenspiegel nähert sich einem Wert an, der dann konstant bleibt.
(iv) Der Medikamentenspiegel bleibt von Anfang an ziemlich konstant.
Welche Meinung ist mathematisch betrachtet richtig?
Lösungen: b) 4
c) ii
(41) Kettenlinie
Hängt man ein homogenes Seil ohne
Biegesteifigkeit an zwei Punkten auf, die sich in
gleicher Höhe befinden, so nimmt es die Gestalt
der sogenannten Kettenlinie an. Unter
bestimmten Voraussetzungen kann sie durch
die Gleichung
x
f(x) =
a (e a
2
e
 ax
)
beschrieben werden.
a)
Beweise die Symmetrie der Funktion.
b)
Begründe, warum der tiefste Punkt des Seils die Koordinaten T(0 / a) besitzt.
c)
Wie groß ist der Durchhang δ des Seils, wenn es an zwei 40 m voneinander
entfernten Punkten aufgehängt wird? (a = 100 m)
2m
(42) Wachstum (linear oder exponentiell)
Vom Graphen eines Wachstumsprozesses sind zwei Punkte bekannt: A(2|4), B(4|6).
a)
Gib die Gleichung der Funktion f(x) an, mit der der Wachstumsprozess beschrieben
werden kann, wenn lineares Wachstum angenommen wird.
b)
y = x+2
Gib die Gleichung der Funktion g(x) an, wenn exponentielles Wachstum
1
angenommen wird.
c)
3
ln( x)
y = 8 e2 2
3
Skizziere die Graphen der beiden Funktionen f und g im Intervall [0;6].
(50) Radioaktive Substanz
Ein radioaktives Präparat zerfällt so, dass die vorhandene Substanz nach jeweils 6 Tagen
auf zwei Drittel der ursprünglichen Menge zurückgeht. Zu Beginn der Messung sind 54 mg
vorhanden.
a)
Durch welche Funktionsart kann der Zerfallsprozess beschrieben werden?
b)
Gib die Termdarstellung der Funktion an.
c)
Wie viele Tage dauert es, bis ca. 1% der ursprünglichen Substanz übrig ist?
 
x
y = 54 32
68,1 d
(64) Halbwertszeit
Ein radioaktiver Stoff der Menge N0 zerfällt nach dem Gesetz N(t) = N0 · e-λt.
N(t) ist die zur Zeit t noch vorhandene Menge des radioaktiven Stoffes, λ ist eine für das
jeweilige Material typische Größe.
Unter der Halbwertszeit τ des Stoffes versteht man jene Zeitspanne, in der die Hälfte des
Materials zerfallen ist.
Begründe, warum die Zahl τ nicht von der ursprünglich vorhandenen Menge abhängt.
(73) Kapital
Jemand möchte auf einem Sparbuch € 7000 längerfristig anlegen.
Eine Sparkasse verspricht ihm, dass sein Kapital nach 10 Jahren bei gleichbleibender
Verzinsung auf € 10 871 angewachsen sein wird.
Wie groß wäre dann der Zinssatz, wenn die Kapitalertragssteuer (KESt) unberücksichtigt
bleibt?
4,5%