LK I Wachstumsmodelle 13

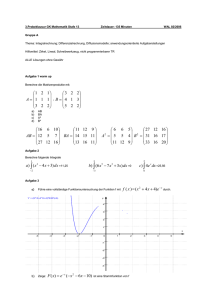
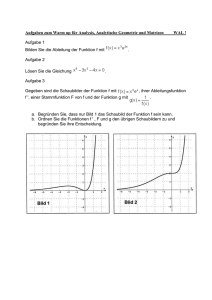
Christianeum
Mathematik
Wilms
Populationsmodelle (4)
LK II
5. 2. 2009
Langzeitentwicklung
Nach den bisher angestellten Betrachtungen ist deutlich geworden, dass die Langzeitentwicklung
einer Population allein von der Übergangsmatrix abhängt. Es stellt sich die Frage, ob und evtl. wie
sich die Übergangsmatrizen „klassifizieren“ lassen, so dass die Entwicklung der Population bereits
aus der Kenntnis der Übergangsmatrix heraus prognostiziert werden kann.
Aufgabe1
Untersuche rechnerisch die Entwicklung einer Population mit der Übergangsmatrix
 0,85
10 
 8,8 
0
0,03 


 
 
0,9 0,03  und den Zustandsvektoren v  10  bzw. w   8,8  .
M =  0


 
 
 0
10 
 8,8 
0,25 0,94 

 
 
Begründe:
 0,88 


M  v  10   0,93 


 1,19 


bzw.
 0,88 


M  w  8,8   0,93


 1,19 


.
Zeilensummenkriterium (Buch, S. 248)
Es sei kein Eintrag einer Übergangsmatrix negativ.
Mathe-INFO
Aufgabe2
(a)
Wenn alle Zeilensummen der Übergangsmatrix größer als 1 sind,
dann expandiert das durch die Übergangsmatrix beschriebene System.
(b)
Wenn alle Zeilensummen der Übergangsmatrix kleiner als 1 sind,
dann zerfällt das durch die Übergangsmatrix beschriebene System.
(c)
Wenn alle Zeilensummen der Übergangsmatrix 1 ergeben,
dann konvergiert das durch die Übergangsmatrix beschriebene System.
Ein System heißt konvergierend, wenn die Einträge in den Zustandsvektoren
sich immer mehr festen Werten (≠ 0 ) nähern.
Ein System heißt divergent, wenn die Entwicklung der Einträge in den
Zustandsvektoren nicht einheitlich verläuft.
Klassifiziere die folgenden Übergangsmatrizen. Stelle zumindest Vermutungen auf.
Überprüfe deine Vermutungen experimentell.
 0,2 0,8
 0,2 0,8
 0,2 0,8 0 
0 
0 






A =  0,3 0 0,6 
B =  0,3 0 0,7 
C =  0,3 0 0,8 






 1

 1

 1

0
0
0
0
0
0






Wir sehen, dass das Zeilensummenkriterium längst nicht immer anwendbar ist. Andererseits haben
wir auf dem Zettel Populationsmodelle (3) ein expandierendes System mit einem Wachstumsfaktor
beschrieben, der ein Eigenwert λ der Übergangsmatrix war mit λ > 1.
Unser Buch (S. 256 – 259) beschreibt einen Weg, wie man mit der Kenntnis der Eigenwerte einer
Matrix eine Aussage über die Entwicklung des Systems treffen kann.
->-> b.w.
Christianeum
Mathematik
Wilms
-2-
________________________________________________________________________________
Eigenwertkriterium (zunächst ohne Beweis)
Es sei L die Übergangsmatrix der Modellentwicklung einer Population.
Aufgabe3
(b)
Genau dann, wenn alle Eigenwerte der Übergangsmatrix vom Betrage her
kleiner als 1 sind, zerfällt das durch die Übergangsmatrix beschriebene
System.
(b)
Genau dann, wenn mindestens ein Eigenwert der Übergangsmatrix vom
Betrage her größer als 1 ist, expandiert das durch die Übergangsmatrix
beschriebene System.
(c)
Genau dann, wenn kein Eigenwert der Übergangsmatrix vom Betrage her
größer als 1 ist und mindestens ein Eigenwert 1 ist, konvergiert das durch die
Übergangsmatrix beschriebene System.
Wende das Eigenwertkriterium auf die Matrizen in der Aufgabe2 an.
Aufgabe4
Betrachtet wird eine Population der Weißbauchmuscheln in den Gewässern vor der Insel
Dickeoog. Diese Tiere durchleben drei gleich lange Phasen: jugendlich, erwachsen, alt. Die Anzahlen der
Exemplare in der jeweiligen Phase denke man sich in dieser Reihenfolge in einem Vektor notiert.
Im Rahmen von Modellrechnungen wird die folgende Leslie-Matrix verwendet:
 0, 2 1 0, 2 


L   0, 4 0
0 
 0 0,5 0 


(a)
Interpretiere jede der von Null verschiedenen Matrixkomponenten vor dem Hintergrund des
Sachkontextes.
(b)
Untersuche das Langzeitverhalten der Modellpopulation.
(c)
Aufgrund der starken Nachfrage nach der Delikatesse Weißbauchmuscheln gibt es Bemühungen,
deren Population zu stabilisieren oder gar zu vergrößern. Ein Weg ist die Reduzierung des
Schiffsverkehrs in den Küstengewässern vor Dickeoog. Diese Reduktion wirkt sich insbesondere auf
die Fruchtbarkeit der Altersgruppe der erwachsenen Muscheln aus. Deshalb soll jetzt die folgende
Matrix untersucht werden:
 0, 2 t 0, 2 


Lt   0, 4 0
0 
 0 0,5 0 


(t > 1)
Man nimmt an, dass es durch die Verminderung des Schiffverkehrs möglich ist, den Parameter t
maximal bis auf den Wert 3 zu vergrößern.
Untersuche, ob es im Modell gelingen kann, die Population langfristig zu stabilisieren. Falls dies
möglich ist, stelle die Populationsentwicklung für diesen Fall über 30 Zeitschritte hinweg (ausgehend
von den Startwerten 500 Jugendliche, 1000 Erwachsene, 2000 Alte) in dem beiliegenden
Koordinatensystem graphisch dar.
Untersuche auch, ob sogar eine Steigerung der Populationsgröße um 5% pro Zeitschritt möglich ist.
Falls diese Ziele (oder eines der beiden) erreichbar sind, bestimme jeweils auch die langfristige
prozentuale Verteilung der Individuen auf die drei Altersklassen.
Aufgabe5
Bearbeite im Buch die Aufgaben S. 251/1–6, S 252/7-8
________________________________________________________________________________
[email protected]