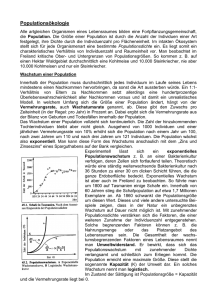
12 Lebenstafeln, Überlebenskurven und Populationswachstums

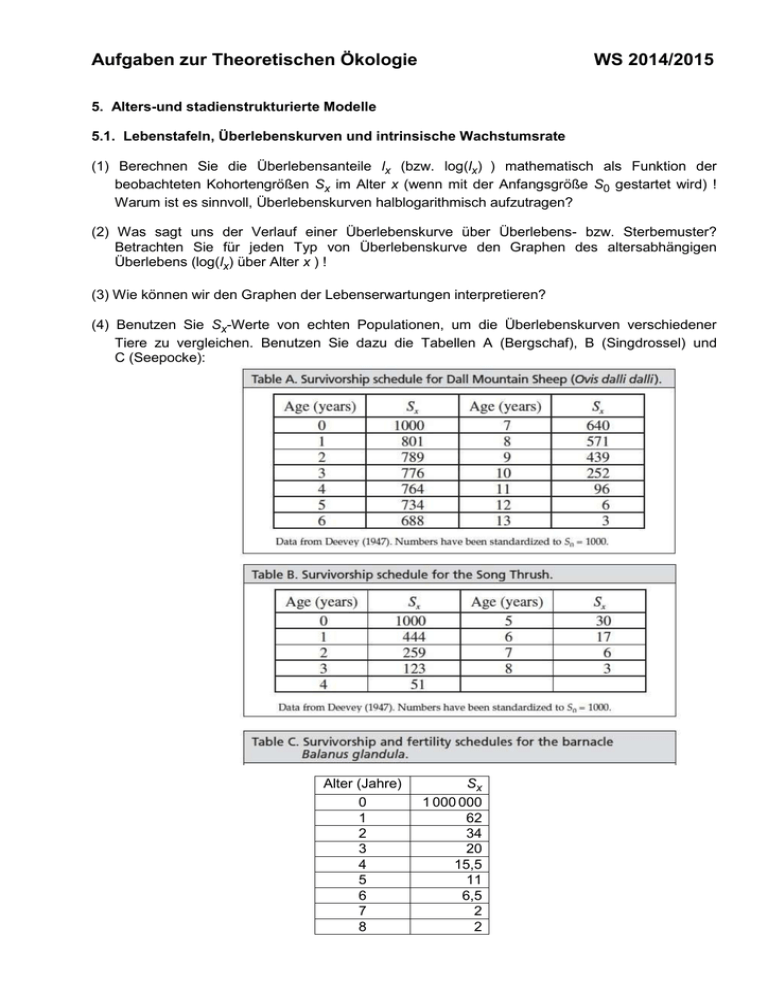
Aufgaben zur Theoretischen Ökologie
WS 2014/2015
5. Alters-und stadienstrukturierte Modelle
5.1. Lebenstafeln, Überlebenskurven und intrinsische Wachstumsrate
(1) Berechnen Sie die Überlebensanteile lx (bzw. log(lx) ) mathematisch als Funktion der
beobachteten Kohortengrößen Sx im Alter x (wenn mit der Anfangsgröße S0 gestartet wird) !
Warum ist es sinnvoll, Überlebenskurven halblogarithmisch aufzutragen?
(2) Was sagt uns der Verlauf einer Überlebenskurve über Überlebens- bzw. Sterbemuster?
Betrachten Sie für jeden Typ von Überlebenskurve den Graphen des altersabhängigen
Überlebens (log(lx) über Alter x ) !
(3) Wie können wir den Graphen der Lebenserwartungen interpretieren?
(4) Benutzen Sie Sx-Werte von echten Populationen, um die Überlebenskurven verschiedener
Tiere zu vergleichen. Benutzen Sie dazu die Tabellen A (Bergschaf), B (Singdrossel) und
C (Seepocke):
Alter (Jahre)
0
1
2
3
4
5
6
7
8
Sx
1 000 000
62
34
20
15,5
11
6,5
2
2
(5) Welchen Effekt hat eine Änderung (Verschiebung oder Dehnung) der altersspezifischen
Fekunditäten (Fruchtbarkeitsverläufe) auf R0 , G und r ?
(6) Welchen Effekt hat eine Änderung der altersspezif. Überlebensraten auf auf R0 , G und r ?
Testen Sie:
Alter (Jahre)
0
1
2
3
4
Sx
1000
500
250
125
0
Alter (Jahre)
0
1
2
3
4
Sx
1000
250
125
100
0
Von welchem Typ sind die Überlebenskurven? Vergleichen Sie die Ergebnisse !
5.2. Alterstrukturierte Matrixmodelle
(1) Untersuchen Sie den Graphen des Populationswachstums (in linearer Skalierung)! Welche
Form hat das Populationswachstum? Ist die Population wachsend, stabil oder abnehmend?
Wie ändert sich der zeitabhängige Wachstumsfaktor Rt mit der Zeit?
(2) Untersuchen Sie Ihr Populationswachstum in halblogarithmischer Darstellung und Ihre
tabellarischen Projektionen (Spalte G). An welchem Punkt der 25 Jahre umfassenden
Projektion ändert sich Rt nicht mehr (oder nur noch wenig) von Jahr zu Jahr? Wenn sich die
Rnicht mit der Zeit ändern, sind sie eine Schätzung der asymptotischen Wachstumsrate R*
(bzw. des Wachstumsfaktors er* der Eulerschen Gleichung). Wie groß ist R* für die gegebene
Population, und wie beeinflußt dies das Populationswachstum? Wie verändert sich R*, wenn
Sie die Einträge in der Leslie-Matrix ändern?
Bemerkung: Bei Rt bitte wenigstens 4 Nachkommastellen berücksichtigen.
(3) Setzen Sie die Parameter der Leslie-Matrix auf die ursprünglichen Werte zurück. Wie ist die
Zusammensetzung der Population (der Anteil der Individuen in den Alterklassen 1, 2, 3 und 4),
wenn die Population eine „stabile“ (d.h. stationäre !!) Verteilung erreicht hat?
(4) Welchen Einfluss hat die anfängliche anzahlmäßige Zusammensetzung auf Rt , R* und die
stabile Altersverteilung? Wie beeinflusst dies Rt und die Altersverteilung vor der Stabilisierung
der Altersverteilung? Verändern Sie die Startverteilung so, daß die Ausgangspopulation aus 75
Individuen in der ersten und je 1 Individuum in den verbleibenden Alterklassen besteht. Stellen
Sie Ihre Ergebnisse graphisch dar und interpretieren Sie diese!. Haben die Ergebnisse
Implikationen die für das Management (bzgl. Naturschutz)?
(5) Wir wollen nun annehmen, daß die Population aus Individuen bestehen möge, die über die
Altersklasse 4 hinaus weiterleben können (Interpretation: „die in Altersklasse 4 verbleiben“).
Angenommen, diese Individuen hätten dieselben Fertilitätsfunktionen (F) wie die vierte
Altersklasse und dazu 25% Wahrscheinlichkeit, jeweils ein weiteres Jahr zu überleben.
Zeichnen Sie das Übergangsdiagramm des Lebenszyklus, und justieren Sie eine veränderte
„Leslie“-Matrix so, daß sie diese älteren Individuen mit einschließt.