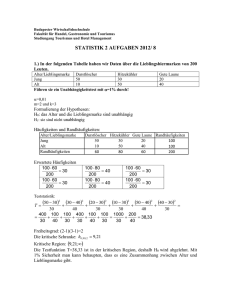
5. Veranstaltung

Einführung in die Software R: Unterstützung für Teilnehmer der
Veranstaltung „Statistische Methodenlehre 1“
5. Veranstaltung 05.12.2000
Unsere Funktion wuerfelsim sah zuletzt so aus (dabei habe ich zwei nicht mehr benötigte
Zeilen, die die horizontale Gerade betrafen herausgenommen.
wuerfelsim<-function(n=100,rel=T,...)
{
stich<-sample(1:6,size=n,replace=T)
hauf<-table(stich)
theo<-rep(n/6,6)
Titel<-“Absolute und erwartete Häufigkeiten“
legende<-c(“Abs. Häufigk.“,“Erw. Häufigk.“)
if(rel==T)
{hauf<-hauf/n
theo<-theo/n
Titel<-“Relative Häufigkeiten und Wahrscheinlichkeiten“
legende<-c(“Rel. Häufigk.“,“Wahrscheinlichkeiten“)
}
hoehe<-rbind(hauf,theo)
print(hoehe,digits=4)
barplot(hoehe,main=Titel,col=c(“red“,“blue“),beside=T,...)
abline(h=0)
mtext(paste(“Stichprobenumfang: n=“,n),font=2)
legend(locator(1),legend=legende,fill=c(“red“,“blue“))
}
Jetzt wollen wir die Funktion so abändern, dass nicht nur ein Würfel simuliert werden kann,
sondern eine beliebige diskrete Verteilung, d.h. wir wollen alle Möglichkeiten der Funktion
sample nutzen und dann mit barplot ein Balkendiagramm der relativen bzw. absoluten
Häufigkeiten zusammen mit den Wahrscheinlichkeiten bzw. erwarteten Häufigkeiten zeichnen.
Wir nennen die Funktion jetzt samplebar. Wir brauchen jetzt also weitere Argumente, um die
Grundgesamtheit und die Wahrscheinlichkeiten festzulegen. Nennen wir die Argumente grund
und wahr. Standardmäßig soll der Würfelwurf simuliert werden, also setzen wir grund=1:6
und alle Werte aus grund sollen, wenn nichts anderes vereinbart wird, mit gleicher
Wahrscheinlichkeit gezogen werden. Daher setzen wir wahr=rep(1,length(grund)), d.h.
die Zahl 1 wird so oft wiederholt, wie es der Länge des Vektors grund entspricht. Dies ist
jedoch keine Wahrscheinlichkeit. Daher wird im ersten Befehl unserer Funktion der Vektor wahr
normiert, indem ich jeden Wert des Vektors wahr durch sum(wahr), also durch die Summe
aller Werte in wahr teile.
In der nächsten Zeile setzen wir jetzt bei sample die Grundgesamtheit grund und die
Wahrscheinlichkeit wahr ein. Die theoretischen Werte ändern sich jetzt, d.h. die erwarteten
Häufigkeiten sind jetzt n*wahr (wenn wir die absoluten Häufigkeiten darstellen) und den
relativen Häufigkeiten entsprechen die Wahrscheinlichkeiten, die durch den Vektor wahr
gegeben sind.
samplebar<function(grund=1:6,n=100,wahr=rep(1,length(grund)),rel=T,...) #
HIER
{
wahr<-wahr/sum(wahr) # HIER
stich<-sample(grund,size=n,replace=T,prob=wahr) # HIER
hauf<-table(stich)
theo<-n*wahr # HIER
Titel<-“Absolute und erwartete Häufigkeiten“
legende<-c(“Abs. Häufigk.“,“Erw. Häufigk.“)
if(rel==T)
{hauf<-hauf/n
theo<-wahr # HIER
Titel<-“Relative Häufigkeiten und Wahrscheinlichkeiten“
legende<-c(“Rel. Häufigk.“,“Wahrscheinlichkeiten“)
}
hoehe<-rbind(hauf,theo)
print(hoehe,digits=4)
barplot(hoehe,main=Titel,col=c(“red“,“blue“),beside=T,...)
abline(h=0)
mtext(paste(“Stichprobenumfang: n=“,n),font=2)
legend(locator(1),legend=legende,fill=c(“red“,“blue“))
}
Wir wollen jetzt unsere Funktion ausprobieren, indem wir alle Argumente variieren. Wir
beobachten, dass sich die beobachteten absoluten Häufigkeiten auf die erwarteten Häufigkeiten
und die relativen Häufigkeiten auf die Wahrscheinlichkeiten einpendeln, wenn wir den
Stichprobenumfang immer weiter vergrößern.Vielleicht möchten wir die Höhe der einzelnen
Balken an die Balken schreiben. Dazu könnten wir die Funktion text verwenden. Dazu müssen
wir die Koordinaten angeben, wo der Text stehen soll. Als x-Koordinate möchten wir die Mitte
der Balken verwenden, als y-Koordianate die Höhe der Balken. Die Höhe der Balken steht in der
Variablen hoehe. Wie bekommen wir die Koordinaten der Mittelpunkte der Balken? Schauen
wir in die Hilfe zu barplot unter Value.
Dort erfahren wir, dass ein Vektor oder eine Matrix mit den Balkenmittelpunkten ausgegeben
wird. Probieren wir das an einem einfachen Beispiel aus. Wir verwenden die Daten der
Arbeitslosen und Sozialhilfeempfänger in Göttinger Bezirken, die wir schon in der vorigen
Veranstaltung benutzt hatten.
barplot(rbind(alos,sozi),beside=T,names=bezirk)
Mit diesem Befehl erhalten wir keine Ausgabe in der Console. Erst mit dem folgenden Befehl
werden diese Werte in dem Objekt mp gespeichert.
> mp<-barplot(rbind(alos,sozi),beside=T,names=bezirk)
> mp
[1,]
[2,]
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5
2.5 5.5 8.5 11.5 14.5 17.5 20.5 23.5
Wir wollen diese Graphik noch etwas verfeinern und dann die Werte an die Balken schreiben.
> title("Arbeitslose und Sozialhilfeempfänger in Göttinger
Bezirken")
> legend(locator(1),legend=c("Anteil Arbeitslose", "Anteil
Sozialhifeempfänger"), fill=c("red","yellow"))
> text(x=mp,y=rbind(alos,sozi),labels=rbind(alos,sozi))
Wir haben absichtlich die Namen der Argumente dazu geschrieben, obwohl es nicht nötig wäre,
da sie in der richtigen Reihenfolge stehen.
Jetzt wird der Text genau in den Balken geschrieben. Wir haben beim letzten Mal schon gesehen,
dass wir mit den Argumenten adj und pos die Position des Textes relativ zum Punkt
beeinflussen können. Mit pos=3 wird der Text oberhalb des Punktes geschrieben. Außerdem
wollen wir ihn fett und etwas größer. Daher:
>text(x=mp,y=rbind(alos,sozi),labels=rbind(alos,sozi),pos=3,font=
2,cex=1.3)
Wenn wir den Text in halber Balkenhöhe wollen, so verwenden wir den Befehl
>text(x=mp,y=rbind(alos,sozi)/2,labels=rbind(alos,sozi),
font=2,cex=1.3)
In der Hilfe zu text erfahren wir unter Details, dass wir den Text auch drehen können mit
dem graphischen Parameter srt. Versuchen wir also den Text nicht waagerecht, sondern
senkrecht in halber Höhe zu schreiben.
Aus der Hilfe zu text:
Schauen wir unter par in der Hilfe nach srt.
Die Drehung des Textes ist also in Grad einzugeben.
> mp<-barplot(rbind(alos,sozi),beside=T,names=bezirk)
> text(x=mp,y=rbind(alos,sozi)/2, labels=rbind(alos,sozi),
font=2, cex=1.3, srt=90)
Wir möchten den Text lieber anders gedreht, also setzen wir srt=270.
> mp<-barplot(rbind(alos,sozi),beside=T,names=bezirk)
> text(x=mp, y=rbind(alos,sozi)/2, labels=rbind(alos,sozi),
font=2, cex=1.3, srt=270)
Mit dieser Darstellung sind wir jetzt zufrieden und bauen eine entsprechende Änderung in unsere
Funktion samplebar ein. Wir haben noch eine Formatangabe für den Text eingefügt, um nicht
zu viele Nachkommastellen zu erhalten.
samplebar<function(grund=1:6,n=100,wahr=rep(1,length(grund)),rel=T,...)
{
wahr<-wahr/sum(wahr)
stich<-sample(grund,size=n,replace=T,prob=wahr)
hauf<-table(stich)
theo<-n*wahr
Titel<-“Absolute und erwartete Häufigkeiten“
legende<-c(“Abs. Häufigk.“,“Erw. Häufigk.“)
if(rel==T)
{hauf<-hauf/n
theo<-wahr
Titel<-“Relative Häufigkeiten und Wahrscheinlichkeiten“
legende<-c(“Rel. Häufigk.“,“Wahrscheinlichkeiten“)
}
hoehe<-rbind(hauf,theo)
print(hoehe,digits=4)
mp<-barplot(hoehe,main=Titel,col=c(“red“,“blue“),beside=T,...) #
HIER
abline(h=0)
mtext(paste(“Stichprobenumfang: n=“,n),font=2)
text(x=mp, y=hoehe/2, labels=format(hoehe, digits=2), font=2,
srt=270) # HIER
legend(locator(1),legend=legende,fill=c(“red“,“blue“))
}
Wir wollen diese Funktion jetzt noch einmal durchtesten. Es empfiehlt sich, zunächst mit den
Standardwerten zu beginnen.
Schließlich wollen wir die Funktion an folgender Grundgesamtheit betrachten. Die Datei
baltj93 enthält die Anzahl der Bewohner der Bundesrepublik Deutschland im Jahre 1993 in
den Altersjahren von 1 bis 95. Die Datei baltj93w enthält nur die weiblichen Bewohner. Die
Dateien galtj93 und galtj93w enthalten die entsprechenden Daten für die Stadt
Göttingen.
baltj93
[1] 718400 729500 742500 761000 734700 746600 713500 699700 664000
[10] 660600 664700 683400 682600 681500 642800 636500 641800 662100
[19] 659600 691000 718400 810400 908600 969700 1070300 1135600 1170000
[28] 1199200 1200300 1216400 1198800 1155500 1134300 1106600 1068600 1021300
[37] 1002500 973600 935700 923000 893000 902300 884600 909400 902800
[46] 851800 802700 731600 627500 820500 834500 816600 980100 1045900
[55] 1028800 968200 909400 889600 860600 805100 656600 656600 670500
[64] 709400 691300 692700 646800 634900 629400 583200 568100 584500
[73] 595500 570300 424300 272800 254800 269000 334800 405600 384600
[82] 360100 313100 287100 257400 222900 190100 157300 126100 103000
[91]
78800
62300
46200
34300
22200
> baltj93w
[1]
[11]
[21]
[31]
[41]
[51]
[61]
[71]
[81]
[91]
349800
323600
353700
575200
440700
408000
331300
357800
265900
60000
355900
332400
398000
555900
445600
398600
334800
368500
251500
48000
361300
332600
444200
548800
437100
480800
344200
381500
221000
35700
370300
332000
470400
534800
448400
514900
366800
370800
206500
26800
358700
313100
571400
516700
442600
507500
359800
277400
187100
17600
363300
308800
547800
493300
416200
479000
363100
180100
163500
346400
311300
563900
484700
392900
451000
353300
168600
140300
340600
321400
576200
471500
358100
443400
363700
180300
117600
323900
320400
573900
455400
308400
430600
374200
227500
93800
321200
339000
582600
452900
402800
404000
363600
279000
77500
> galtj93
[1] 1196 1207 1238 1193
[16] 947 908 954 1013
[31] 3249 2851 2811 2535
[46] 1424 1268 1204 1042
[61] 953 936 982 1043
[76] 463 496 585 695
[91] 190 136 110
77
1137
1403
2393
1406
1027
836
54
1188
1988
2099
1476
1047
773
1045
2807
2008
1317
1048
785
1050
3394
1911
1568
1002
664
990 972 978 1065 985
3853 4340 4466 4284 4136
1874 1755 1611 1546 1609
1663 1631 1517 1394 1393
1096 959 960 990 1010
596 544 479 373 359
957 935
3712 3482
1505 1510
1260 1227
1026 757
282 216
> galtj93w
[1] 546 621 614 564 565 568 515 491 462 459 462 506 498 486 481
[16] 470 437 491 501 804 1149 1544 1792 1932 2183 2184 1954 1883 1667 1594
[31] 1489 1265 1345 1179 1100 952 928 892 895 852 757 715 769 710 723
[46] 700 623 601 509 686 728 635 791 835 846 738 672 736 670 643
[61] 500 499 526 555 570 584 581 595 649 606 657 672 698 682 513
[76] 340 337 400 483 580 536 534 463 434 374 345 292 263 213 156
[91] 153 107
89
55
42
Als Grundgesamtheit grund verwenden wir die Zahlen von 1 bis 95. Für das Argument wahr
verwenden wir z.B. baltj93. Wir erinnern uns, dass dieser Vektor durch unsere Funktion
normiert wird.
samplebar(grund=1:95,wahr=baltj93,n=100000)
Wir sehen jetzt, dass unsere Ausgabe bei großer Grundgesamtheit und großem n einige Nachteile
hat. Wir wollen also den Text in die Balken nur wahlweise schreiben lassen und die Ausgabe des
Stichprobenumfangs formatieren.
samplebar<function(grund=1:6,n=100,wahr=rep(1,length(grund)),rel=T,
Text=T,...) # HIER
{
wahr<-wahr/sum(wahr)
stich<-sample(grund,size=n,replace=T,prob=wahr)
hauf<-table(stich)
theo<-n*wahr
Titel<-“Absolute und erwartete Häufigkeiten“
legende<-c(“Abs. Häufigk.“,“Erw. Häufigk.“)
if(rel==T)
{hauf<-hauf/n
theo<-wahr
Titel<-“Relative Häufigkeiten und Wahrscheinlichkeiten“
legende<-c(“Rel. Häufigk.“,“Wahrscheinlichkeiten“)
}
hoehe<-rbind(hauf,theo)
print(hoehe,digits=4)
mp<-barplot(hoehe,main=Titel,col=c(“red“,“blue“),beside=T,...)
abline(h=0)
mtext(paste(“Stichprobenumfang:
n=“,formatC(n,format=“f“,digits=0)),font=2) # HIER
if(Text==T) # HIER
{
text(x=mp, y=hoehe/2, labels=format(hoehe, digits=2), font=2,
srt=270) # HIER
}
legend(locator(1),legend=legende,fill=c(“red“,“blue“))
}
Wir probieren unsere Funktion jetzt aus:
samplebar(grund=1:95,wahr=baltj93,n=100000,Text=F)
Wir wollen die Arbeit an der Funktion samplebar jetzt beenden, jedoch noch die
Altersverteilungen mit der Funktion barplot in Gestalt einer Alterspyramide darstellen. Wir
hatten nur die Altersverteilung aller Bewohner und die der weiblichen Bewohner. Berechnen wir
uns also die Altersverteilung der männlichen Bevölkerung:
baltj93m<-baltj93-baltj93w
galtj93m<-galtj93-galtj93w
Die Dateien baltj93m und galtj93m enthalten also die Anzahlen der männlichen Bewohner
in der Bundesrepublik Deutschland bzw. in Göttingen im Jahre 1993.
> barplot(baltj93)
> barplot(baltj93,names=1:95)
> barplot(baltj93,names=1:95,col="red")
> barplot(baltj93m,names=1:95,col="red")
> barplot(baltj93w,names=1:95,col="red")
Wir wollen jetzt die Verteilung des Alters für Männer und Frauen gemeinsam sehen, dabei soll
eine Gruppe (Männer oder Frauen) nach unten abgetragen werden. Dabei ist es in R so, dass
negative Werte für das Argument height nach unten abgetragen werden. Wir wollen die
Balken direkt untereinander, nicht nebeneinander. Deshalb ist es naheliegend, zunächst zu
versuchen, das Argument beside=F zu setzen. Jetzt muss man verstehen, wie R in diesem Fall
rechnet. Ist beside=F gesetzt (es ist vorausgesetzt, dass height eine Matrix ist), so werden
die Teilbalken entsprechend den Werten in den Spalten der Matrix bei positiven Werten
übereinander gesetzt, d.h. zu dem Wert in der ersten Zeilen wird der Wert der zweiten Zeile
(gleiche Spalte) dazuaddiert. Folgende Eingabe liefert nicht das gewünschte Resultat:
> barplot(rbind(baltj93w,-baltj93m),names=1:95)
Richtig wäre:
> barplot(rbind(baltj93w,-baltj93),names=1:95)
Wir zeichnen noch eine horizontale Linie bei Null mit dem folgenden Befehl:
> abline(h=0,col=2)
Es gelingt jedoch nicht, die Balken in unterschiedlichen Farben darzustellen. Deshalb setzen wir
das Argument beside=T und versuchen dann mit dem Argument space den Abstand zu
regulieren.
> barplot(rbind(baltj93w,-baltj93m),col=c(2,3),beside=T)
Um besser zu sehen, was passiert, verwenden wir ein kleines künstliches Beispiel.
> barplot(rbind(1:6,-(6:1)),col=c(2,3),beside=T)
Jetzt werden die negativen Balken direkt rechts neben die Balken für die positiven Balken für 1:6
nach unten gezeichnet. Er muss also um eine Einheit zurückgesetzt werden. Standardmäßig gilt
space=c(0,1). Die erste Zahl steht für den Abstand innerhalb der Gruppen. Das gewünschte
Resultat erhalten wir mit:
> barplot(rbind(1:6,-(6:1)),col=c(2,3),beside=T,space=c(-1,1))
> barplot(rbind(baltj93w,-baltj93m),col=c(2,3),beside=T,space=c(1,1),names=1:95)
Um die Balken horizontal zu erhalten, setzen wir das Argument horiz=T.
barplot(rbind(baltj93w,-baltj93m),col=c(2,3),beside=T,space=c(1,1),names=1:95,horiz=T)
Wir teilen die Werte durch 1000, um eine angenehmere Beschriftung der x-Achse zu erhalten.
Wir beschriften die Graphik mit der Funktion mtext, die Text an den Rand (margin) schreibt.
Mit dem Argument adj bestimmen wir die Position des Textes.
> barplot(rbind(baltj93w,-baltj93m)/1000, col=c(2,3), beside=T,
space=c(-1,1), names=1:95, horiz=T)
> mtext(text="Männer",adj=0.25,col=3,cex=1.5)
> mtext(text="Frauen",adj=0.75,col=2,cex=1.5)
Wir wollen die Altersverteilung in der Bundesrepublik Deutschland vergleichen mit der
Altersverteilung in Göttingen und möchten beide Graphiken nebeneinander sehen. Dazu
verwenden wir den graphischen Parameter mfrow=c(1,2). Das bedeutet, dass unser
Graphikfenster in eine Zeile und 2 Spalten aufgeteilt wird, die sukzessive gefüllt werden (siehe
Hilfe zu par.
> par(mfrow=c(1,2))
> barplot(rbind(baltj93w,-baltj93m)/1000, col=c(2,3), beside=T,
space=c(-1,1), names=1:95, horiz=T)
> mtext(text="Männer",adj=0.25,col=3)
> mtext(text="Frauen",adj=0.75,col=2)
> title(main="Bundesrepublik")
> barplot(rbind(galtj93w,-galtj93m)/1000, col=c(2,3), beside=T,
space=c(-1,1), names=1:95, horiz=T)
> mtext(text="Männer",adj=0.25,col=3)
> mtext(text="Frauen",adj=0.75,col=2)
> title(main="Göttingen")