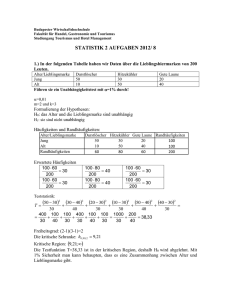
Einführung in die Software R: Unterstützung für Teilnehmer der

Einführung in die Software R: Unterstützung für Teilnehmer der
Veranstaltung „Statistische Methodenlehre 1“
3. Veranstaltung 14.11.2000
In der letzten Veranstaltung ging etwa der folgende Befehl nicht:
> plot(sin,-pi,2*pi,cex=2)
Mit dem Argument cex=2 wollten wir die Achsenbeschriftung vergrößern. Nicht alle
graphischen Parameter kann man innerhalb der Funktion plot verwenden. Folgende
Befehlsfolge wirkt:
> par(cex=2)
> plot(sin,-pi,2*pi)
Mit der Funktion par werden graphische Parameter vereinbart (siehe Hilfe) oder rufen Sie
> par()
auf, um einen Eindruck zu bekommen, welche Möglichkeiten es zur Gestaltung einer Graphik
gibt.
Wir wollten eine Funktion schreiben, um dieselben Eingaben nicht ständig wiederholen zu
müssen. Ganz einfache Funktionen können Sie in der R-Console schreiben. Für größere
Funktionen empfiehlt sich die Benutzung eines Editors. Wir schreiben zunächst einige kleinere
Funktionen in der R-Console.
xquadrat<-function(x)
{
xquadrat<-x*x
xquadrat}
Die Funktion xquadrat berechnet das Quadrat von x. Die letzte Zeile ist unbedingt nötig, um
eine Ausgabe zu erzielen.
> xquadrat(2)
[1] 4
> xquadrat(3)
[1] 9
> plot(xquadrat,-4,4) # Plottet die Funktion y=x2 von –4 bis 4
Wir wollen jetzt eine Funktion schreiben, die ein beliebiges Polynom zweiten Grades berechnet.
>polynom<-function(x=0,a=0,b=0,c=1)
{
y<-a+b*x+c*x^2
y
}
> polynom(2,2,-1,3)# Berechnet y=2-x+3x2 an der Stelle x=2
[1] 12
> polynom(-5:5,2,-1,3) # Berechnet y=2-x+3x2 für x=-5, -4, -3, ...,5
[1] 82 54 32 16
6
2
4 12 26 46 72
Wir wollen jetzt eine Funktion schreiben, die ein Polynom plottet. Innerhalb einer Funktion
können wir wohl selbstgeschriebene als auch in R implementierte Funktionen verwenden. Im
folgenden Beispiel verwenden wir polynom und plot. Wir wollen eine Funktion schreiben,
die für variable Koeffizienten a, b und c ein Polynom y=a+bx+cx2 berechnet und als Graphik in
einem x,y-Koordinatensystem darstellt. Wir schreiben diese Funktion mit einem Editor z.B. mit
Word oder Wordpad.
Wir geben der Funktion den Namen polyplot. Dies geschieht durch die übliche
Namenszuweisung mit dem Kleiner- und Minus-Zeichen. Auf der rechten Seite steht zunächst
function.
polyplot<-function
Damit wird vereinbart, dass polyplot eine Funktion sein soll. In runden Klammern werden
dann die Namen der Argumente vereinbart. Überlegen wir uns, welche Argumente diese Funktion
haben soll. Sie soll ein beliebiges Polynom zweiten Grades y=a+bx+cx2 berechnen und in einem
bestimmten Bereich zeichnen. Also brauchen wir als Argumente unserer Funktion zunächst die
Parameter des Polynoms, d.h.
polyplot<-function(a,b,c
Des weiteren müssen wir den Bereich festlegen, über dem das Polynom gezeichnet werden soll.
Wir verwenden ein Intervall. Das Polynom soll von der unteren Intervallgrenze bis zur oberen
Intervallgrenze gezeichnet werden, d.h. von und bis sind die weiteren Argumente unserer
Funktion. Die erste Zeile sieht also so aus:
polyplot<-function(a,b,c,von,bis)
Die Befehle, die diese Funktion ausführen soll, werden dann, eingeschlossen in geschweifte
Klammern, in die nächsten Zeilen geschrieben, d.h. das Grundgerüst unserer Funktion ist das
folgende:
polyplot<-function(a,b,c,von,bis)
{
}
Wir müssen jetzt die geschweiften Klammern füllen. Was soll unsere Funktion machen? Sie soll
schließlich unser Polynom zeichnen. Wir können leider nicht den Befehl
plot(function, from, to)
verwenden (z.B. hatten wir plot(log,1,10)) verwenden. Dies geht jedoch nicht mit der
Fumktion polynom, die wir gerade geschrieben haben, da sie noch von den Argumenten a, b
und c abhängt. Deshalb definieren wir uns, wie wir das in der ersten Veranstaltung getan haben,
eine Folge von x-Werten, für die wir dann als y-Wert den Wert des Polynoms berechnen. Die
Folge der x-Werte definieren wir mit dem Befehl seq, dieser Befehl hat die Argumente (siehe
Hilfe) from, to und length. Die Bedeutung dieser Argumente ist durch ihren Namen erklärt.
polyplot<-function(a,b,c,von,bis)
{
x<-seq(from=von, to=bis, length=1000)
}
Wir berechnen jetzt für diese x-Werte das Polynom y=a+bx+cx2. Dazu benutzen wir unsere
Funktion polynom, der wir die Argumente x, a, b und c übergeben.
polyplot<-function(a,b,c,von,bis)
{
x<-seq(from=von, to=bis, length=1000)
y<-polynom(x,a,b,c)
}
Jetzt schreiben wir noch den Plotbefehl in unsere Funktion.
polyplot<-function(a,b,c,von,bis)
{
x<-seq(from=von, to=bis, length=1000)
y<-polynom(x,a,b,c)
plot(x,y,type=”l”)
}
Die Funktion ist jetzt fertig. Sie ist zunächst in die R-Console zu kopieren, d.h sie ist in Word zu
markieren und zu kopieren und wird dann in R eingefügt. Geben Sie
polyplot
ein, um sich zu überzeugen, dass die Funktion in R jetzt vorhanden ist. Sie kann jetzt so
aufgerufen werden:
polyplot(a=0,b=1,c=2,von=-4,bis=5)
oder gleichwertig ohne Namen der Argumente:
polyplot(0,1,2,-4,5)
Die folgende Graphik zeigt das Ergebnis.
Wir haben bei der Defintion der Funktion polyplot in der Zeile
polyplot<-function(a,b,c,von,bis)
nur die Namen der Argumente geschrieben. Wir haben den Argumenten keine Standardwerte
zugewiesen, d.h. alle Argumente sind verlangte Argumente, müssen also bei jedem Aufruf der
Funktion angegeben werden. Standardwerte werden mit dem Gleichheitszeichen und einem
folgenden Wert zugewiesen. Durch die Zeile
polyplot<-function(a=0,b=0,c=1,von=-3,bis=3)
wird also a und b der Wert 0, c der Wert 1, von der Wert –3 und bis der Wert 3
zugwiesen. Folgendes ist also die endgültige Version unserer Funktion polyplot.
polyplot<-function(a=0,b=0,c=1,von=-3,bis=3)
{
x<-seq(from=von, to=bis, length=1000)
y<-polynom(x,a,b,c)
plot(x,y,type=”l”)
}
Bei Eingabe von
polyplot()
werden also die Standardwerte verwendet, d.h. es wird das Polynom y=x2 von –3 bis 3
gezeichnet.
polyplot(2,-1,3,-5,5) # Zeichnet y=2-x+3x2 von x=-5 bis x=5
Wir wollen unsere Graphik etwas verfeinern und beschriften, d.h. einige der graphischen
Parameter, die wir in der letzten Veranstaltung kennengelernt haben, verwenden, so soll z.B. die
Kurve rot und in Linienstärke 3 gezeichnet werden. Außerdem soll unsere Graphik einen Titel
und eine andere y-Achsenbeschriftung erhalten. Probieren wir die Eingabe (wir verwenden die
Defaultwerte für a, b, c, von und bis):
polyplot(main=”Normalparabel”,ylab=”f(x)”,col=”red”,lwd=4)
Wir erhalten die Fehlermeldung:
Error in polyplot(main = "Normalparabel", ylab = "f(x)", col =
"red", :
unused argument(s) (main ...)
Die graphischen Parameter stehen also nicht zur Verfügung. Um das zu erreichen, brauchen wir
nur in der Definitionszeile nach den Argumenten drei Punkte ... einzufügen. Das gleiche
machen wir beim Aufruf der Funktion plot. Damit können wir alle Argumente zu plot auch
in unserer Funktion polyplot verwenden.
polyplot<-function(a=0,b=0,c=1,von=-3,bis=3,...)
{
x<-seq(from=von, to=bis, length=1000)
y<-polynom(x,a,b,c)
plot(x,y,type=”l”,...)
}
Ein erneuter Aufruf von
polyplot(main=”Normalparabel”,ylab=”f(x)”,col=”red”,lwd=4)
ergibt die folgende Graphik:
Eine alternative Defintion unserer Funktion polyplot ist die folgende:
polyplot<-function(a=0,b=0,c=1,von=-3,bis=3,...)
{
polyx<-function(x)
{
polyx<-polynom(x,a,b,c)
}
plot(polyx,von,bis,...)
}
Hier haben wir innerhalb der Funktion polyplot eine Funktion polyx definiert durch die
Anweisungen innerhalb der folgenden geschweiften Klammern. Diese Funktion hat nur x als
Argument und übernimmt die Werte von a, b und c. Jetzt haben wir eine völlig festgelegte
Funktion (keine R-Funktion, sondern eine mathemaische Funktion, die für jedes x den
Funktionswert f(x) berechnet), die wir nach dem Muster
plot(function, from, to)
zeichnen können.
Wir hatten beim letzten Mal den Befehl
barplot(table(sample(6,size=1000,replace=T))/1000)
verwendet. Dabei wurde mit sample eine Stichprobe aus den ganzen Zahlen von 1 bis 6 der
Größe 1000 mit Zurücklegen gezogen. Mit table werden die Häufigkeiten für die Werte 1 bis
6 ausgezählt. Wir dividieren durch 1000 und berechnen damit die relativen Häufigkeiten. Die
Funktion barplot zeichnet ein Balkendiagramm. Das Ergebnis ist ähnlich wie das von
plot(table(sample(6,size=1000,replace=T))/1000,type="h")
Wir verwenden weiterhin die Funktion barplot, wollen die Graphik aber etwas verfeinern,
insbesondere den Stichprobenumfang als Argument eingeben können. Außerdem wollen wir
durch ein Argument entscheiden können, ob die relativen oder absoluten Häufigkeiten dargestellt
werden sollen. Schließlich soll auch die Verwendung graphischer Parameter möglich sein.
Nennen wir unsere Funktion wuerfelsim. Als Argumente verwenden wir n für die
Stichprobengröße und rel. Mit rel wollen wir festlegen, ob die relativen oder absoluten
Häufigkeiten dargestellt werden sollen. Damit hat rel eine ähnliche Funktion wie replace
in der Funktion sample. Es ist also eine logische Variable, die die Werte True und False
annehmen kann. Wir verwenden True als Defaultwert, d.h. zeichnen die relativen Häufigkeiten.
Das Grundgerüst unserer Funktion sieht also so aus:
wuerfelsim<-function(n=100,rel=T,...)
{
}
Jetzt füllen wir die Klammern, beginnen mit dem Ziehen der Stichprobe.
wuerfelsim<-function(n=100,rel=T,...)
{
stich<-sample(1:6,size=n,replace=T)
hauf<-table(stich)
hori<-n/6
Titel<-“Balkendiagramm der absoluten Häufigkeiten“
if(rel==T)
{hauf<-hauf/n
hori<-1/6
Titel<-“Balkendiagramm der relativen Häufigkeiten“
}
print(hauf)
barplot(hauf,main=Titel,...)
abline(h=0)
abline(h=hori,lwd=3,col=“blue“)
}
Wir haben nicht erklärt, was in den einzelnen Schritten getan wird. Wir wollen das als
Kommentare hinter die Befehle schreiben. Wichtige Funktionen sollten Sie stets mit
Kommentaren versehen, damit Sie Ihre Funktionen auch später noch verstehen.
wuerfelsim<-function(n=100,rel=T,...) # Definition der Funktion
{
stich<-sample(1:6,size=n,replace=T) # Ziehen der Stichprobe
hauf<-table(stich) # Auszählen der Häufigkeiten
hori<-n/6 # bei hori eine horizontale Linie
Titel<-“Balkendiagramm der absoluten Häufigkeiten“ # Titel
if(rel==T) # wenn rel Wahr ist, dann das folgende
{hauf<-hauf/n # relative Häufigkeiten
hori<-1/6 # Linie bei 1/6 statt 1/6
Titel<-“Balkendiagramm der relativen Häufigkeiten“ # Titel
}
print(hauf) # drucke Tabelle der Häufigkeiten
barplot(hauf,main=Titel,...) # zeichne barplot
abline(h=0) # zeichne x-Achse
abline(h=hori,lwd=3,col=“blue“) # ziehe Horizontale bei hori
}
Mit dem Befehl
wuerfelsim()
erhalten wir die Standardausgabe unserer Funktion, das Balkendiagramm der relativen
Häufigkeiten für n=100 Simulationen eines fairen Würfels. Da uns die Balken zu dicht sind,
können wir das Argument space von barplot verwenden, um den Abstand der Balken zu
regulieren.
wuerfelsim(space=2)
erzeugt größere Abstände zwischen den Balken. Mit
wuerfelsim(n=1000, rel=F, space=2)
wird ein Balkendiagramm der absoluten Häufigkeiten beim Stichprobenumfang n=1000
gezeichnet.
Wir möchten vielleicht noch Text in unsere Graphik schreiben. Vielleicht den
Stichprobenumfang vermerken. Die beiden folgenden Befehle schreiben den Text n=1000 an eine
mit Mausklick bestimmbare Position. Im zweiten Fall wird die Schrift größer.
> text(locator(1),"n=1000")
> text(locator(1),"n=1000",cex=2)
Beim nächsten Mal werden wir lernen, wie man solchen Text in Abhängigkeit vom Argument n
in die Graphik schreiben kann. Wir werden die Graphik noch etwas verfeinern.