Lösungen von Aufgaben 8

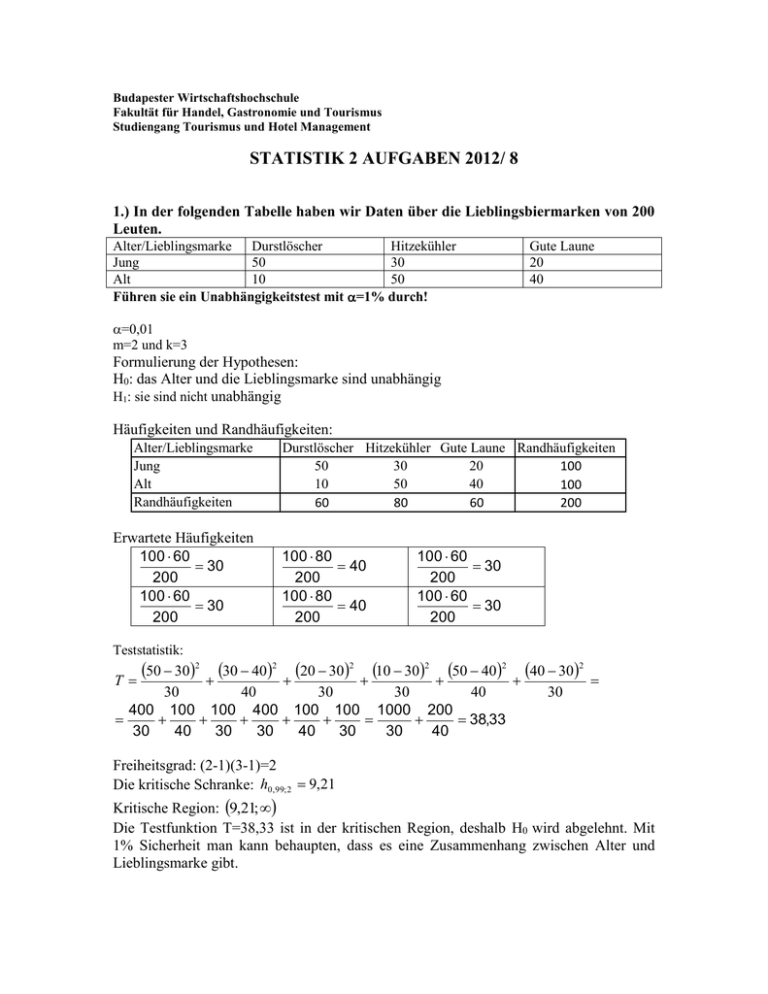
Budapester Wirtschaftshochschule
Fakultät für Handel, Gastronomie und Tourismus
Studiengang Tourismus und Hotel Management
STATISTIK 2 AUFGABEN 2012/ 8
1.) In der folgenden Tabelle haben wir Daten über die Lieblingsbiermarken von 200
Leuten.
Alter/Lieblingsmarke Durstlöscher
Hitzekühler
Jung
50
30
Alt
10
50
Führen sie ein Unabhängigkeitstest mit =1% durch!
Gute Laune
20
40
=0,01
m=2 und k=3
Formulierung der Hypothesen:
H0: das Alter und die Lieblingsmarke sind unabhängig
H1: sie sind nicht unabhängig
Häufigkeiten und Randhäufigkeiten:
Alter/Lieblingsmarke
Jung
Alt
Randhäufigkeiten
Erwartete Häufigkeiten
100  60
 30
200
100  60
 30
200
Durstlöscher Hitzekühler Gute Laune Randhäufigkeiten
50
30
20
100
10
50
40
100
60
80
60
200
100  80
 40
200
100  80
 40
200
100  60
 30
200
100  60
 30
200
Teststatistik:
T
50  302  30  402  20  302  10  302  50  402  40  302
30
40
30
30
40
400 100 100 400 100 100 1000 200








 38,33
30
40
30
30
40
30
30
40
Freiheitsgrad: (2-1)(3-1)=2
Die kritische Schranke: h0,99; 2  9,21
30

Kritische Region: 9,21; 
Die Testfunktion T=38,33 ist in der kritischen Region, deshalb H0 wird abgelehnt. Mit
1% Sicherheit man kann behaupten, dass es eine Zusammenhang zwischen Alter und
Lieblingsmarke gibt.
2.) Anlässlich der Fußballeuropameisterschaft möchte die Illustrierte "Neue Zeit" prüfen,
ob Fussball immer noch ein reiner "Männersport" ist. Die Leserinnen und Leser sind
aufgefordert in der Redaktion anzurufen und anzugeben, ob ihr Interesse "sehr
groß/gross", "mittelmässig" oder "klein/ nicht vorhanden" ist. Nach drei harten Tagen hat
die Praktikantin Frau Meyer 1182 Anrufen entgegengenommen und erstellt folgende
Tabelle:
Interesse Geschlecht
Frauen Männer
sehr gross/gross
95
320
mittelmässig
160
154
klein/ nicht vorhanden 155
298
Ist das Interesse an Fussball unabhängig vom Geschlecht? (Signifikanzniveau 5%)
=0,05
m=3 und k=2
Formulierung der Hypothesen:
H0: die Interesse und das Geschlecht sind unabhängig
H1: sie sind nicht unabhängig
Häufigkeiten und Randhäufigkeiten:
Interesse/Geschlecht
Sehr gross/gross
Mittelmässig
Klein/nicht vorhanden
Randhäufigkeiten
Erwartete Häufigkeiten
410  415
 144
1182
410  314
 108,9
1182
410  453
 157,1
1182
Teststatistik: T 
Männer
320
154
298
772
Frauen
95
160
155
410
Randhäufigkeiten
415
314
453
1182
772  415
 271
1182
772  314
 205,1
1182
772  453
 295,9
1182
95  1442  160  108,92  155  157,12  320  2712
144

108,9
154  205,12  298  295,92
205,1
Freiheitsgrad: (3-1)(2-1)=2
Die kritische Schranke: h0,95; 2  5,99
Kritische Region: 5,99; 
295,9
157,1
 62,3
271

Die Testfunktion T=62,3 ist in der kritischen Region, deshalb H0 wird abgelehnt. Mit 5%
Sicherheit man kann behaupten, dass es eine Zusammenhang zwischen Interesse an
Fussball und Geschlecht gibt.
3.) 20 Firmen wurden über ihren Jahreseinkommen (M Ft) befragt. Wir interessieren uns
für die Verteilung der Einkommen. Kann man bei =5% behaupten, dass die Einkommen
einer Normalverteilung mit dem Erwartungswert 100 M Ft und der Varianz 25 M Ft
folgen?
99
93
101
98
90
103
96
97
105
102
109
89
97
91
102
93
98
97
100
98
H0: das Einkommen der Firmen ist N(100,52)
H1: das Einkommen der Firmen ist nicht N(100,52)
n=20
=0,05
Sei X: das Einkommen einer Firma
Wir wissen, dass X~N(100,52)
Wir haben 20 Beobachtungen, also 4 Klassen kann man bilden. Es ist nicht Nötig, die
Quartile als Grenzpunkte zu wählen, eine mögliche Einteilung ist die folgende:
<95
95- b.u. 100 100- b.u. 105 105Häufigkeiten
5
8
5
2
Erwartete Häufigkeiten 0,1587*20= 0,3413*20= 0,3413*20= 0,1587*20=3,17
3,17
6,83
6,83
 X  100 95  100 
P( X  95)  P

   1  1  1  1  0,8413  0,1587
5
5


1
 95  100 X  100 100  100 
P(95  X  100)  P


  0   1   0,1587  0,3413
5
5
5
2


P(100  X  105)  P(105  X  100)  0,3413
P(105  X )  P( X  95)  0,1587
Teststatistik:
(5  3,17) 2 (8  6,83) 2 (5  6,83) 2 (2  3,17) 2
T



 2,18
3,17
6,83
6,83
3,17
Kein Parameter war geschätzt, so der Freiheitsgrad ist 4-1=3.
Die kritische Schranke: h0,95;3  7,81
Kritische Region: 7,81; 
Die Testfunktion T=2,18 ist nicht in der kritischen Region, deshalb H0 wird nicht
abgelehnt. Mit 5% Sicherheit man kann behaupten, dass das Einkommen der Firmen
N(100,52) ist.
4.) Wir haben 100 vermutlich normalverteilte Zufallszahlen wie folgendes klassifiziert.
Intervall
0-bis unter 0,25
0,25-bis unter 0,5
0,5-bis unter 0,75
Häufigkeit
28
22
19
Können wir die Nullhypothese (Normalverteilung) bei =10% verwerfen?
0,75-bis unter 1
31
n=100
=0,1
Klassenmitten: 0,125
x
ˆ 
0,375
0,625
0,875
28  0,125  22  0,375  19  0,625  31  0,875
 0,5075
100
28  (0,125  0,5075) 2  ...  31  (0,875  0,5075) 2
 0,3
100  1
Also wir können die Werte runden und N(0,5;0,32) anpassen. Die erwartete Häufigkeiten
(vergessen wir es nicht, dass man alle reelle Zahlen einteilen soll):
Intervall
bis unter 0,25 0,25-bis unter 0,5
0,5-bis unter 0,75
0,75Wahrscheinlichkeit
0,2033
0,2967
0,2967
0,2033
Erwartete Häufigkeit
20,33
29,67
29,67
20,33
 X  0,5 0,25  0,5 
 5
P( X  0,25)  P

      1  0,83  1  0,7967  0,2033
0,3 
 6
 0,3
Teststatistik:
(28  20,33) 2 (22  29,67) 2 (19  29,67) 2 (31  20,33) 2
T



 14,31
20,33
29,67
29,67
20,33
Wir haben 2 Parameter geschätzt, so der Freiheitsgrad ist 4-1-2=1.
Die kritische Schranke: h0,9;1  2,71
Kritische Region: 2,71; 
Die Testfunktion T=14,31 ist in der kritischen Region, deshalb H0 wird abgelehnt. Mit
10% Sicherheit man kann behaupten, dass die Daten nicht Normalverteilt sind.