Konzentration I

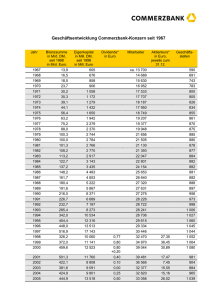
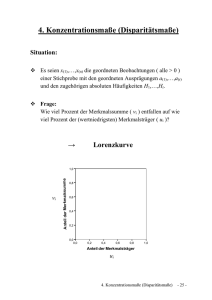
6. Konzentration
6.1 Konzentrationsbegriff
Konzentration im wirtschaftlichen Sinne:
 Ballung von Verfügungsmacht bei einer oder wenigen Wirtschafts-
einheiten (Anzahlaspekt),
 Existenz erheblicher Größenunterschiede (Disparität).
Beispiel 6.1:
 Sind in einem Markt nur wenige Anbieter vorhanden, dann liegt eine
Konzentration vor (Anzahlaspekt).
 Auch bei vielen Anbietern würde man von einer Konzentration
sprechen, wenn die Umsatzanteile der Unternehmen in den
Größenklassen sehr unterschiedlich sind (Disparität).

Abbildung 6.1: Relative und absolute Konzentration
Konzentrationsmaße
absolut
relativ
Messung des Anzahlaspekts
Messung der Größenunterschiede
(Disparität)
Konzentrationsmessung:
- Verteilung der Merkmalssumme auf die Merkmalsträger,
- Abgrenzung des relevanten Marktes (Voraussetzung)
Extremsituationen:
1. Egalitäre Verteilung („Gleichverteilung“):
Situation der minimalen Konzentration:
Jeder Merkmalsträger den gleichen Merkmalsbetrag und damit auch den
gleichen Merkmalsanteil aufweist.
2. Vollkommene Ungleichheit:
Situation der maximalen Konzentration:
Ein Merkmalsträger vereinigt die gesamte Merkmalssumme auf sich,
während die übrigen statistischen Einheiten "Nullträger" sind.
Abbildung 6.2: Konzentrationsmaße
Konzentrationsmaße
absolut
relativ
Konzentrationsraten
Lorenzkurve
Konzentrationskurve
Gini-Koeffizient
Herfindahl-Index
Exponentialindex
6.2 Konzentrationsraten und Konzentrationskurve
Konzentrationsraten: Maße der absoluten Konzentration
 Messung der Wettbewerbsintensität und Konzentrationstendenzen in
der Wirtschaft
Gesetz gegen Wettbewerbsbeschränkungen (GWB)
§19 Abs. 3: kritische Konzentrationsraten (Vermutung einer
marktbeherrschenden Stellung)
Tabelle 6.1: Marktbeherrschende Stellung nach § 19 GWB
 Anzahl der
Unternehmen…
1
 3 oder weniger
 5 oder weniger
 … mit einer Konzentrationsrate
von mind…
 1/3
 1/2
 2/3
Bestimmung von Konzentrationsraten
Konzentrationsmerkmals X (Umsatz, Absatz, Beschäftigte, Börsenwert
etc.) in Form von Einzelbeobachtungen
Merkmalsbeträge: x1 , x 2 , , x n .
Geordnete Reihe (in absteigender Reihenfolge): x
(1)
 x (2)   x (n )
Merkmalsanteil des i-ten Merkmalsträgers:
(6.1)
x (i )
ci 
S
Merkmalssumme:
n
(6.2)
n
S   x i   x (i ) .
i 1
i 1
Konzentrationsraten (kumulierten Merkmalsanteile):
i
(6.3)
Ci   c j Ci 1  ci .
j1
Die Konzentrationsrate Ci gibt an, welchen Merkmalsanteil die i "größten" Unternehmen auf sich vereinigen.
Eigenschaft (ohne „Nullträger“):
(6.4)
0  C1  C 2    C n  1
Konzentrationskurve:
Verbindungslinie der Punkte 0,0, 1, C1 , 2, C 2 ,  ) (=Polygonzug) in
einem kartesischem Koordinatensystem
Abbildung 6.3: Konzentrationskurve
Ci
C3=1
C2
C1
0
1
2
3
i
Minimale Konzentration:
Alle Merkmalsträger haben den gleichen Merkmalsbetrag xi und den
gleichen Merkmalsanteil ci: ci 
1
, i=1,2,…,n
n
Konzentrationskurve: Gerade mit Steigung 1/n
Maximale Konzentration:
Ein Merkmalsträger hält den gesamten Merkmalsbetrag (100% des
Merkmalsbetrags); übrige Merkmalsträger sind „Nullträger“
Merkmalsanteile: c1 = 1, c2 = c3 = …, cn = 0
Abbildung 6.4: Konzentrationskurve bei minimaler und maximaler
Konzentration
Ci
Ci
C3=1
1
C2=2/3
C1=1/3
0
1
2
a) minimale Konzentration (n = 3)
3 i
0
1
2
3 i
b) maximale Konzentration (n = 3)
Eine empirsch ermittelte Konzentrationskurve liegt stets zwischen den
beiden Extremzuständen. Je weiter die Kurve von der sich bei minimaler
Konzentration ergebenden Geraden abweicht, desto stärker ist die
Konzentration ausgeprägt.
Darstellung der Konzentrationskurve bei einer großen Anzahl von
Merkmalsträgern:
a) nur aus Konzentrationsraten der „größten“ Merkmalsträgern oder
b) wie a), jedoch Vervollständigung durch eine unterbrochene Verbindungslinie
Beispiel 6.2a:
In einer Branche treten 10 Unternehmen als Anbieter auf. Die beiden
Großunternehmen erzielen einen Jahresumsatz in Höhe von 250 Mill. €
und 200 Mill. €, während die Umsätze der drei mittelständischen
Unternehmen 45 Mill. €, 50 Mill. € und 40 Mill. € betragen. Die kleineren
Unternehmen erreichen dagegen zusammen nur einen Umsatz von
45 Mill. €.
Merkmalssumme der zehn Unternehmen:
10
S   x i  250  200  45  50  40  45  630 Mill. € .
i 1
Geordnete Reihe (geordneten Umsätze) der fünf größten Unternehmen:
x 1  250, x 2  200, x 3  50, x 4  45, x 5  40,
Merkmalsanteile (= Marktanteile):
x (1) 250
x (2) 200
c1 

 0,397 ; c 2 

 0,317 ;
S
630
S
630
x (3)
50
x ( 4)
45
c3 

 0,079 , c 4 

 0,071;
S
630
S
630
x (5)
40
c5 

 0,063
S
630
Konzentrationsraten:
C1
C2
C3
C4
C5
 c1  0,397 ,
 C1  c 2  0,397  0,317  0,714 ,
 C 2  c 3  0,714  0,079  0,793 ,
 C 3  c 4  0,793  0,071  0,864 ,
 C 4  c 5  0,864  0,063  0,927
Vermutung einer marktbeherrschenden Stellung nach § 19 GWB:
C1  0,397  1 / 3 , ebenfalls C 3  0,793  0,5 und C 5  0,927  2 / 3
Konzentrationskurve (mit unterbrochener Verbindungslinie):
Ci
(10;1)
1
(4;0,864)
(5;0,927)
(3;0,793)
0,75
(2;0,714)
0,5
(1;0,397)
0,25
0
1
2
3
4
5
6
7
8
9
10 i

Beispiel 6.2b:
Nehmen wir an, für die kleineren Unternehmen lägen auch Umsatzzahlen vor:
10 Mill. € , 5 Mill € , 20 Mill. € , 8 Mill. € und 2 Mill. € .
Vollständige geordnete Reihe,
x 1  250, x 2  200, x 3  50, x 4  45, x 5  40,
x 6  20, x 7   10, x 8  8, x 9  5, x 10  2,
Merkmalsanteile:
c6
c9
x (6) 20


 0,032,
S
630
x (9 )
5


 0,008,
S
630
x (7) 10
c7 

 0,016,
S
630
x (10)
2
c10 

 0,003
S
630
x (8)
8
c8 

 0,013,
S
630
Konzentrationsraten:
 C5  c6  0,927  0,032  0,959 ,
 C6  c7  0,959  0,016  0,975 ,
 C7  c8  0,975  0,013  0,988 ,
 C8  c9  0,988  0,008  0,996 ,
 C9  c10  0,996  0,003  1.
C6
C7
C8
C9
C10
Vollständige Konzentrationskurve:
Ci
1
(10;1)
(8;0,988)
(6;0,959)
(4;0,864)
(3;0,793)
(9;0,996)
(5;0,927) (7;0,975)
0,75
(2;0,714)
0,5
(1;0,397)
0,25
0
1
2
3
4
5
6
7
8
9
10 i
Vergleich beider Konzenrationskurven:
Ausmaß der Konzentration ist entscheidend durch die großen und
mittleren Unternehmen geprägt.

6.3 Herfindahl-Index
Konzentrationsraten:
- statischer Einblick in die Konzentration auf einem Markt,
- Vergleiche von Konzentrationen schwierig (Konzentrationskurven
können sich schneiden),
Herfindahl-Index: globale Maßzahl der abs. Konzentration
n
(6.5)
K H   c i2 .
i 1
Summe der quadrierten Merkmalsanteile c i
Approximativer Herfindahl-Index (falls die Merkmalsbeträge nur für n1
bedeutendsten Merkmalsträger vorliegen):
n1
(6.6)
K ' H   c i2
i 1
Darstellung als gewogenes arithmetisches Mittel
n
(6.7)
K H   c i  g i mit g i  ci
i 1
Gewichtung der Merkmalsanteile mit sich selbst
Wertebereich des Herfindahl-Index
Minimale Konzentration (ci = 1/n für alle i):
n 2
n  1 2 n 1
1
1
K H   ci      
 n
 (untere Schranke)
2
n2 n
i 1
i 1 n 
i 1 n
Maximale Konzentration (c1 = 1, c2 = c3 = …, cn = 0):
n 2
K H   c i  12  0 2    0 2  1 (obere Schranke).
i 1
Der Herfindahl-Index K H liegt im Intervall 1/n  K H  1 . Je höher sein
Wert, desto stärker ist die Konzentration ausgeprägt.
Interpretation von KH unter Bezug zu den US-Fusionsrichtlinien:
Tabelle 6.2: US-Fusionsrichtlinien
Konzentrationsgrad
Niedrig
Mittelhoch
Hoch
1968
C 4  0,5
0,5  C 4  0,7
C 4  0,7
1982
K H  0,1
0,1  K H  0,18
K H  0,18
Beispiel 6.3:
Unter Verwendung der fünf größten Unternehmen lässt sich der
Herfindahl-Index näherungsweise mit Formel (6.6) bestimmen:
n1  5
K ' H   c i2  0,397 2  0,317 2  0,0792  0,0712  0,0632
i 1
 0,1576  0,1005  0,0062  0,0050  0,0040  0,273 .
Wenn alle Merkmalsanteile bekannt sind, würde man aber den exakten
Koeffizienten mit Formel (6.5) ermitteln. Sein genauer Wert
unterscheidet sich von der näherungsweisen Berechnung nur auf der
dritten Nachkommastelle:
10 2
K H   ci  0,3972  0,3172  0,0792  0,0712  0,0632  0,0322
i 1
2
2
2
2
 0,016  0,013  0,008  0,003  0,1576  0,1005  0,0062
 0,0050  0,0040  0,0010  0,0003  0,0002  0,0001  0,0000
 0,275 .
Die geringsten fünf Merkmalsanteile, deren Wert noch quadriert wird,
sind nämlich kleiner oder gleich 0,032. Nach den US-Fusionsrichtlinien
von 1982 ist die vorliegende Konzentration als "hoch" zu bewerten
( K H  0,275  0,18 ).

Beziehung zwischen Herfindahl-Index und dem Variationskoeffizienten v:
(6.8)
v2  1
KH 
n
Anzahlaspekt:
K H nimmt zu, wenn die Anzahl der Merkmalsträger (n) sinkt
Disparität:
K H nimmt zu, wenn die relative Streuung des Konzentrationsmerkmals
steigt
Als Maß der absoluten Konzentration fängt der Herfindahl-Index Aspekte
der relativen Konzentration mit ein.
Unterschiedliche Auswirkungen von
relative und absolute Konzentration:
Konzentrationsvorgängen
auf
z.B. Konzentration durch Fusion von Unternehmen
Fusionen vergrößern die absolute Konzentration, nicht notwendig jedoch
auch die Disparität
Auswirkung einer Fusion auf KH:
Fusion zweier Unternehmen i und h mit den Markanteilen ci und ch
vor der Fusion:
nach der Fusion:
Gesamtbeitrag der beiden
Unternehmen i und h zu KH:
Gesamtbeitrag der beiden
Unternehmen i und h zu KH:
ci2  c 2h
(ci  c h ) 2  ci2  2ci c h  c 2h
Resultat: KH steigt ceteris paribus nach der Fusion der beiden
Unternehmen um den Betrag 2ci c h an.
Herleitung der Formel (6.8):
Wir setzen die Gleichungen (6.1) und (6.2) in die Berechnungsformel des
Herfindahl-Indexes (6.5) ein:

i  2

x 
.
K H   ci2 
 x i 


Mit x
i 2  x 2 und ( x )2  (n  x)2  n 2  x 2 erhält man
i
i
2
2
x
x i 
KH  
n2  x2

i .
2 2
n x
2
2
und nach Erweiterung mit  nx  nx ( 0)
KH 
Aufgrund
x i2  nx 2  nx 2
2
n x
des
2
.
Varianzverschiebungssatzes,
s2 
1 2
x i  x 2 ,
n
gilt
ns 2  x i2  nx 2 , was eine Vereinfachung des Zählers mit sich bringt:
KH 
ns 2  nx 2
2
n x
2
.
2
Dividiert man nun den Zähler und Nenner durch n  x , erhält man
2 2
K H 
s
x 1
n
und mit der Formel für den Variationskoeffizienten v  s x schließlich
Gleichung (6.8):
(s x ) 2  1 v 2  1
KH 

.
n
n
Beispiel 6.4:
Auf einem Markt für Spezialmaschinen sind vier Unternehmen tätig, von
denen jedes einen Absatz von 20 Stück erzielt. Wie verändert sich der
Herfindahl-Index, wenn jeweils zwei Unternehmen fusionieren?
Aus der folgenden Tabelle geht hervor, dass die Streuungen vor und
nach der Fusion null sind. Durch die Fusion wird hier also nicht die
Disparität berührt. Der Anstieg des Herfindahl-Indexes ist damit
ausschließlich auf den Anzahlaspekt zurückzuführen.
vor der Fusion
 Arithmetisches Mittel:
1 4
1
x    x i  (20  20  20  20)  20
4 i 1
4
 Varianz:
1 4
s 2    x i  x 2
4 i 1
nach der Fusion
 Arithmetisches Mittel:
1 2
1
x    x i  (40  40)  40
2 i 1
2
 Varianz:
1 2
s 2    x i  x 2
2 i 1

(20  20) 2  (20  20) 2 ]  0
 Variationskoeffizient:
 Variationskoeffizient:
v
s
0
v 
0
x 20
 Herfindahl-Index:
2
v 1 0 1
KH 

 0,25
n
4

1
  40  402  40  402  0
2
1
 [(20  20) 2  (20  20) 2 
4
s
0

0
x 40
 Herfindahl-Index:
2
KH 
v 1 0 1

 0,5
n
2

Beispiel 6.5:
Vergleichen wir zwei Märkte, auf denen zwei Unternehmen konkurrieren.
Die Marktanteile beim Umsatz liegen bei 0,60 und 0,40 sowie 0,70 und
0,30. Der höhere Herfindahl-Index auf dem zweiten Markt wird hier
aufgrund der gleichen Anzahl von Unternehmen allein durch den
Disparitätsaspekt bedingt:
2
2
2
2
 Markt 1: K H   c i  0,6  0,4  0,52
i 1
2 2
2
2
 Markt 2: K H   c i  0,7  0,3  0,58 .
i 1

6.4 Rosenbluth-Index
Der Rosenbluth-Index KR misst das Ausmaß
Konzentration mit Bezug auf die Konzentrationskurve.
der
absoluten
Der Rosenbluth-Index ist durch die Fläche A (s. Abbildung) oberhalb der
Konzentrations-kurve K (=Dekonzentrationsfläche) innerhalb des
Rechtecks 0BCD bestimmt.
Abbildung: Konzentrationskurve und Dekonzentrationsfläche
Ci
1
D
C
A3
C2
A2
C1
A
F
K
E
A1
B
0
1
2
n=3
i
Fläche der Dekonzentration:
Je größer die Fläche A ist, desto geringer ist die absolute Konzentration.
Da wir nicht die Dekonzentration, sondern die Konzentration messen, ist
der Rosenbluth-Index als inverse Funktion der Fläche A definiert:
(6.9)
KR = (2A)-1
Die Definition (6.9) stellt sicher, dass KR, Intervall (0; 1] liegt:
KR  0: fehlende Konzentration (Dekonzentration)
KR = 1/n: minimale Konzentration
KR = 1: maximale Konzentration
Abbildung: Dekonzentrationsfläche A
Ci
1
D
C
A3
C2
F
A
A2
C1
K
E
A1
B
0
1
2
n=3
g
g h Höhe)
h, g Grundseite,
A1: Dreiecksfläche
h, g Grundseite,
2 (FD =
 Fläche A1: Dreiecksfläche (FD =
 Fläche
2
c
0 1
A1 = 1 1 =
c1 = 0,5c1
2
2
 Fläche A2: Trapezfläche (FT =
i
h Höhe)
(wegen c1 = C1)
gG
h, g kleine Grundseite, G große
2
Grundseite, h Höhe)
A2 =
1 2
c2 = 1,5c2
2
(wegen c2 = C1 - C2)
 Fläche A3: Trapezfläche
A2 =
23
c3 = 2,5c3
2
(wegen c3 = C2 - C3)
 allgemein: Fläche Ai: Trapezfläche
Ai =
(i - 1)  i
2i - 1
ci =
ci
2
2
(wegen ci = Ci-1 – Ci)
Fläche A (straffierte Fläche oberhalb der Konzentrationskurve K):
n
(6.10)
n 2i  1
1 n
A   Ai  
 c i   (2i  1)  c i
2
2 i 1
i 1
i 1
n
1 n
1 n
1
  2  i  ci   ci   i  ci 
2 i 1
2 i 1
2
 i 1
1
 Minimale Konzentration
Abbildung: Dekonzentrationsfläche bei minimaler Konzentration
Ci
1
D
C
A
C2
K
C1
B
0
1
2
n=3
i
Minimale Konzentration (= maximale Dekonzentrationsfläche):
Dreiecksfläche 0CD: Amax =
1
n
n =
2
2
 Maximale Konzentration
Abbildung: Dekonzentrationsfläche bei maximaler Konzentration
Ci
1
D
E
C
A
K
B
0
1
2
n=3
i
Maximale Konzentration (minimale Dekonzentrationsfläche):
Dreiecksfläche 0ED: Amin =
1
2
 Dekonzentrationsfläche und Rosenbluth-Index
Fläche A als Maß der Dekonzentration:
Je größer (kleiner) die Fläche A, desto niedriger (größer) die
Konzentration
Wertebereich der Dekonzentrationsfläche A:
1
n
A
2
2
Übergang zu einem Konzentrationsmaß  reziproker Wert 1/A
Wertebereich von A-1: 2  A
-1

2
2
A2
oder
n
n
Damit das Konzentrationsmaß zwischen 0 und 1 liegt (Normierung) liegt,
verwendet man nicht den Kehrwert der Fläche A, 1/A, sondern den
reziproken Wert der doppelten Fläche A. Das sich auf diese Weise
ergebende Konzentrationsmaß ist der in (6.9) definierte RosenbluthIndex KR.
Eine Rechenformel für den Rosenbluth-Index erhält man aus der
Flächenberechnung (6.10):
(6.11)
KR 
1
n
2  i  ci  1
i 1
Beispiel 6.2c:
Der Rosenbluth-Index soll für die Branche berechnet werden, in der 10
Unternehmen miteinander konkurrieren. Die Merkmalsanteile (=
Marktanteile) ci sind zur Darstellung der Konzentrationskurve ermittelt
worden.
Zunächst berechnen wir die im Nenner der Formel (6.11) stehende
Summe in einer Arbeitstabelle:
i
1
2
3
4
5
6
7
8
9
10

ci
0,397
0,317
0,079
0,071
0,063
0,032
0,016
0,013
0,008
0,003
ici
0,397
0,634
0,237
0,284
0,315
0,192
0,112
0,104
0,072
0,030
2,377
KR 
1
10
2  i  ci  1

1
2  2,377  1
i 1

1
 0,266
3,754