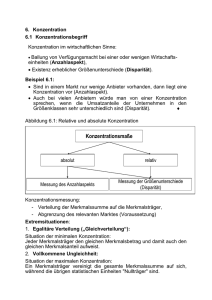
Beispiele aus dem täglichen Leben

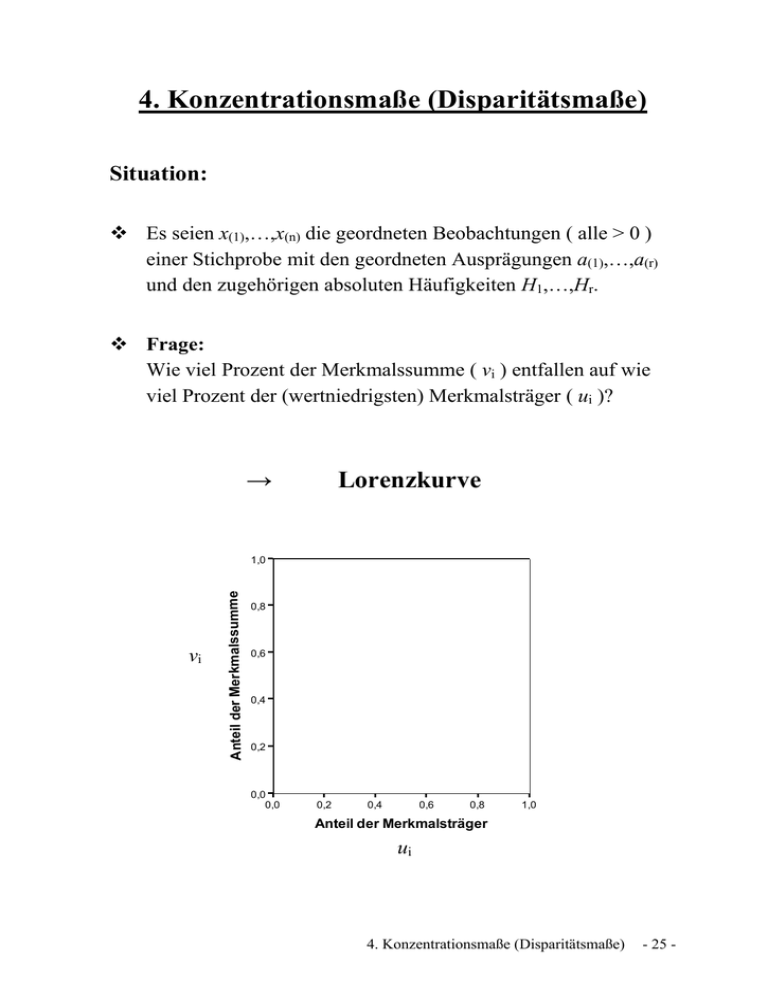
4. Konzentrationsmaße (Disparitätsmaße)
Situation:
 Es seien x(1),…,x(n) die geordneten Beobachtungen ( alle > 0 )
einer Stichprobe mit den geordneten Ausprägungen a(1),…,a(r)
und den zugehörigen absoluten Häufigkeiten H1,…,Hr.
 Frage:
Wie viel Prozent der Merkmalssumme ( vi ) entfallen auf wie
viel Prozent der (wertniedrigsten) Merkmalsträger ( ui )?
→
Lorenzkurve
vi
Anteil der Merkm alssumme
1,0
0,8
0,6
0,4
0,2
0,0
0,0
0,2
0,4
0,6
0,8
1,0
Anteil der Merkmalsträger
ui
4. Konzentrationsmaße (Disparitätsmaße)
- 25 -
 Beispiel: 5-maliges Würfeln, n = 5
0,0
1,0
x(j)
ui
vi
1
1
2
2
4
1/5 = 0,2
2/5 = 0,4
3/5 = 0,6
4/5 = 0,8
1
1/10 = 0,1
2/10 = 0,2
4/10 = 0,4
6/10 = 0,6
1
Anteil der Merkm alssumme
gemäß (I.)
0,8
1,0

0,6

0,4

0,2

0,6
0,4
0,2
0,1

0,0
0,0
∑ = 10
0,2
0,4
0,6
0,8
1,0
Anteil der Merkmalsträger
 Oder einfacher gemäß (II.) (Arbeitstabelle):
a(j)
Hj
ui
a(j) Hj
vi
1
2
4
2
2
1
2/5 = 0,4
4/5 = 0,8
1
2
4
4
2/10 = 0,2
6/10 = 0,6
1
∑ = 5 ( = n)
∑ = 10
0,0
1,0
Anteil der Merkm alssumme
1,0
0,8

0,6
0,6
0,4

0,2
0,2

0,0
0,0
0,2
0,4
0,6
0,8
1,0
Anteil der Merkmalsträger
4. Konzentrationsmaße (Disparitätsmaße)
- 26 -
Extremfälle:
 Keine Konzentration:
 Alle Merkmalsträger haben den gleichen Anteil an der
Merkmalssumme, d.h. auf α∙100% der Untersuchungseinheiten entfallen α∙100% der Merkmalssumme (0 ≤ α ≤ 1).
 Beispiel: Auf 10%, 20%,…,100% der befragten Haushalte
entfallen 10%, 20%,…,100% des angegebenen Vermögens.
 Die Lorenzkurve ist die Diagonale.
 Vollständige Konzentration:
 Ein Merkmalsträger vereinigt auf sich die gesamte
Merkmalssumme; alle übrigen haben keinen Anteil.
 Beispiel: Ein Haushalt verfügt über das gesamte
angegebene Vermögen. Alle anderen haben nix.
 Die Lorenzkurve verläuft bis zum Punkt ((n-1)/n, 0) auf der
Abszisse (x-Achse) und steigt dann fast senkrecht auf bis
zum Punkt (1, 1).
 Damit ist offensichtlich:
 Die Lorenzkurve ist eine graphische Darstellung für die
Ungleichheit der Verteilung.
 Je näher die Lorenzkurve an der Diagonalen liegt, um so
geringer ist die Konzentration, je weiter sie sich davon
entfernt, um so größer ist die Konzentration.
4. Konzentrationsmaße (Disparitätsmaße)
- 27 -
Beispiel: Anzahl der Beschäftigten in kleinen
Handwerksbetrieben, Vergleich zweier Regionen
 Merkmalsträger: Handwerksbetriebe
 Merkmal:
Anzahl der Beschäftigten
Altenkirchen
Wittgenstein
Anzahl der
Beschäftigten a(j)
Anzahl der
Betriebe Hj
Anzahl der
Beschäftigten a(j)
Anzahl der
Betriebe Hj
1
2
3
30
40
30
1
2
3
120
40
40
∑ = 100
∑ = 200
 Arbeitstabellen:
Altenkirchen
a(j)
Hj
ui
a(j) Hj
vi
1
2
3
30
40
30
30/100 = 0,3
70/100 = 0,7
1
30
80
90
30/200 = 0,15
110/200 = 0,55
1
∑ = 100
∑ = 200
Wittgenstein
a(j)
Hj
ui
a(j) Hj
vi
1
2
3
120
40
40
120/200 = 0,6
160/200 = 0,8
1
120
80
120
120/320 = 0,375
200/320 = 0,625
1
∑ = 200
∑ = 320
4. Konzentrationsmaße (Disparitätsmaße)
- 28 -
Altenkirchen
a(j)
Hj
ui
a(j) Hj
vi
1
2
3
30
40
30
30/100 = 0,3
70/100 = 0,7
1
30
80
90
30/200 = 0,15
110/200 = 0,55
1
∑ = 100
∑ = 200
Wittgenstein
a(j)
Hj
ui
a(j) Hj
vi
1
2
3
120
40
40
120/200 = 0,6
160/200 = 0,8
1
120
80
120
120/320 = 0,375
200/320 = 0,625
1
∑ = 200
∑ = 320
1,0
0,0


1,0
Region
Anteil der Beschäftigten
0,9

Altenkirchen

Wittgenstein
0,8
0,6
0,7
0,6

0,6
1,0

0,0
0,5
0,4

0,4
0,3
0,2

0,2
0,1


0,0
0,0 0,1
0,2
0,3
0,4
0,5 0,6
0,7
0,8
0,9
1,0
Anteil der Handwerksbetriebe
Frage:
In welcher Region ist die Konzentration (Ungleichheit der
Verteilung) größer?
Gesucht: Maß für die Ungleichheit der Verteilung.
4. Konzentrationsmaße (Disparitätsmaße)
- 29 -