FORMELSAMMLUNG STATISTIK - Fakultät WiSo Uni Hamburg

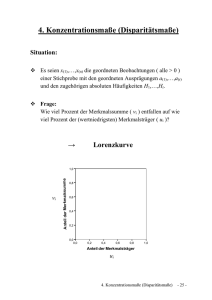
Statistik I / B. Ziegler
Formelsammlung
FORMELSAMMLUNG STATISTIK (I)
Statistische Formeln, Definitionen und Erläuterungen
A
qualitatives Merkmal
ai
Merkmalsausprägung
X
quantitatives Merkmal
xi
Merkmalswert
N
Anzahl der statistischen Einheiten in der Grundgesamtheit
n
Stichprobenumfang
hi
absolute Häufigkeit von xi (alternativ: ni)
fi
relative Häufigkeit von xi (alternativ: ni/n)
Hi
kumulierte absolute Häufigkeit
Fi
kumulierte relative Häufigkeit
xu
i
xo
i
Untergrenze der i-ten Klasse
∆xi
Breite der i-ten Klasse: ∆xi = xio - xu
i
x*
i
Mitte der i-ten Klasse: xi* =
k
Anzahl der Klassen
Obergrenze der i-ten Klasse
xio + xui
2
F( xu
) kumulierte relative Häufigkeit an der Untergrenze der Klasse i
i
F( xio ) kumulierte relative Häufigkeit an der Obergrenze der Klasse i
x
arithmetisches Mittel (alternativ: µ)
Z
Zentralwert (Median)
D
Häufigster Wert (dichtester Wert, Modus bzw. Modalwert)
xp
Prozentpunkt
F(x)
Anteil der Merkmalswerte X < x
Statistik I / B. Ziegler
1.
Histogramm
Histogramm
Die Häufigkeitsverteilung quantitativ-stetiger Merkmale wird als Histogramm
dargestellt. Bei konstanter Klassenbreite ∆xi sind die Rechteckhöhen proportional
zu den relativen (oder absoluten) Klassenhäufigkeiten.
Bei ungleichen Klassenbreiten ermittelt man die Rechteckhöhen, indem die
relativen (oder absoluten) Klassenhäufigkeiten fi (bzw hi) durch die jeweiligen
Klassenbreiten ∆xi dividiert werden:
fi
∆xi
di =
Dadurch wird gewährleistet, daß die relative (bzw. absolute) Häufigkeit einer
Klasse gleich der Rechteckfläche über dieser Klasse ist.
2.
Verteilungsfunktion (Summenhäufigkeitsfunktion) quantitativ-stetiger
Merkmale
F(x i ) = f (x < x i )
Berechnung von Anteilswerten innerhalb einer Klasse
x−x
F (x ) = F (x ) +
∆x
u
i
u
i
⋅ fi
i
Das Konzept der p-Quantile
xp = x +
u
i
( ) ⋅ ∆x
F(x p ) − F x iu
fi
i
2
Statistik I / B. Ziegler
3.
Mittelwerte
Mittelwerte (auch als Lageparameter bezeichnet)
Mittelwerte sind statistische Maßzahlen, die die durchschnittliche Lage ("Mitte")
der Merkmalswerte einer Häufigkeitsverteilung wiedergeben. Eine sinnvolle
Berechnung ist nur bei eingipfeligen Verteilungen möglich.
3.1.
Das arithmetische Mittel
x ist ein rechentypischer Mittelwert, d.h. jeder Merkmalswert xi beeinflußt seinen
Wert. x gibt an, welchen Merkmalswert jede statistische Einheit (Merkmalsträger)
haben würde, wenn die gesamte Merkmalssumme gleichmäßig auf alle statistischen
Einheiten verteilt wäre (Ersatzwert).
a) Ungruppierte Daten
N
∑x
x = i=1
i
=
N
1 N
⋅ xi
N
∑
i=1
b) Gruppierte Daten
k
∑ xi ⋅ hi
x = i=1
N
=
k
∑ xi ⋅ fi
i=1
bei Klassenbildung
k
∑ xi* ⋅ hi
x = i=1
N
=
k
∑ xi* ⋅ fi
i=1
3
Statistik I / B. Ziegler
3.2.
Mittelwerte
Der Zentralwert (Median)
Werden alle statistischen Einheiten nach der Größe ihres Merkmalswertes geordnet,
so ist der Zentralwert (Z) der Wert der mittleren statistischen Einheit, d.h. 50
Prozent aller statistischen Einheiten haben einen Merkmalswert kleiner oder gleich
dem Zentralwert und 50 Prozent haben einen Merkmalswert größer oder gleich dem
Zentralwert. Der Median ist somit der 50-Prozentpunkt.
a) Ungruppierte Daten
Z = x N+1
bei N = ungerade
2
(x N + x N )
bei N = gerade
2
Z=
2
+1
2
b) Klassifizierte Daten
Zunächst: Aufsuchen der Klasse i in der
Fi = 0,5 (Einfallsklasse von Z)
Z = xui +
( ) ⋅x
(
F( x ) − F( x )
0,5 − F xui
0
i
u
i
0
i
)
− xiu = xui +
( ) ⋅ ∆x
0,5 − F xui
fi
i
Anmerkung:
Wird die "Trennung" zwischen dem oberen und dem unteren Abschnitt der
Häufigkeitsverteilung nicht im Verhältnis 1 : 1 (wie beim Zentralwert), sondern im
Verhältnis 1 : 3 bzw. 3 : 1 vollzogen, so spricht man vom Quartil 1 (= 25Prozentpunkt) bzw. Quartil 3 (=75-Prozentpunkt).
Die entsprechenden Formeln für klassifizierte Daten lauten:
Suche die Klasse, in der Fi = 0,25 (bzw. 0,75) wird
3.3.
Q1 =
xui
Q3 =
xui
+
+
( ) ⋅ ∆x
0,25 − F xui
fi
i
( ) ⋅ ∆x
bzw.
0,75 − F xui
fi
i
Der häufigste Wert, der auch als dichtester Wert oder Modus bezeichnet wird, ist
der Merkmalswert mit der größten absoluten bzw relativen Häufigkeit.
D = xi mit i aus hmax
bzw. fimax
i
Bei klassifizierten Daten wird als häufigster Wert die Klassenmitte xi* der Klasse
mit der größten absoluten bzw. relativen Häufigkeit bestimmt unter der Annahme
konstanter Klassenbreiten. Im Falle ungleicher Klassenbreiten wird die
max
Klassenmitte der Klasse mit der größten Häufigkeitsdichte (di ) genommen.
4
Statistik I / B. Ziegler
3.4.
Mittelwerte
Geometrisches Mittel
a) Ungruppierte Daten
G = N x 1 ⋅ x 2 ⋅ x 3 ....x N
bzw.
log G =
1 N
⋅ ∑ log x i
N i =1
b) Gruppierte Daten
h
G = N x1 1 ⋅ x 2
h2
h
⋅ x 3 3 ....x k
hk
bzw.
1 k
log G = ⋅ ∑ h i log x i
N i =1
3.5.
Formale Eigenschaften der Mittelwerte
Der Zentralwert besitzt die formale Eigenschaft, daß die Summe der absoluten
Abweichungen der Merkmalswerte vom Zentralwert geringer ist als von
irgendeinem anderen Wert:
N
∑
i=1
x i - Z = min.
Im Gegensatz zum Zentralwert gelten für das arithmetische Mittel folgende formale
Eigenschaften:
a) die Summe der Abweichungen der Merkmalswerte vom arithmetischen Mittel ist
Null:
N
∑ (x
i
- x) = 0
i=1
b) die Summe der quadrierten Abweichungen der Merkmalswerte von x ist kleiner
als von jedem anderen Wert:
N
∑ (x
i
- x)
2
= min.
i=1
Relation zwischen den Mittelwerten:
D = Z = x symmetrische Verteilung
D > Z > x rechtssteile Verteilung
D < Z < x linkssteile Verteilung
5
Statistik I / B. Ziegler
Streuungsmaße
4.
Streuungsmaße
Streuungsmaße lassen erkennen, ob sich die Merkmalswerte eng um einen
Mittelwert gruppieren oder stark streuen. Sie messen somit die Abweichungen der
einzelnen Merkmalswerte von ihrem Mittelwert.
4.1.
Spannweite
Die Spannweite (R) ist die Differenz zwischen dem größten und dem kleinsten
Merkmalswert einer Verteilung:
R = xmax
- xmin
i
i
Bei klassifizierten Daten lassen sich entsprechend die Klassengrenzen der
Randklassen verwenden.
4.2.
Mittlere (bzw. durchschnittliche) absolute Abweichung
Die mittlere absolute Abweichung (d) ist das arithmetische Mittel der absoluten
Abstände der Merkmalswerte von einem Mittelwert (meist x zuweilen aber auch
Z)
a) Ungruppierte Daten
N
d=
∑x
- x
i
i=1
=
N
N
1
⋅
N
∑x
1
⋅
N
∑x -Z
- x
i
i=1
N
d=
∑x
- Z
i
i=1
=
N
N
i
i=1
b) Gruppierte Daten
k
d=
∑x
- x ⋅ hi
N
k
d=
i
i =1
∑
i=1
x
*
i - x ⋅ hi
N
k
=
∑x
i
- x ⋅ fi
i=1
k
=
∑ xi*
- x ⋅ fi
i=1
Entsprechendes gilt, wenn für x der Zentralwert eingesetzt wird.
6
Statistik I / B. Ziegler
Streuungsmaße
4.3.
Varianz und Standardabweichung
der
Die Varianz und die daraus hergeleitete Standardabweichung sind die
gebräuchlichsten Streuungsmaße.
Die Varianz (σ2) ist die durchschnittliche Abweichung der quadrierten Abstände
Merkmalswerte vom arithmetischen Mittel.
a) Ungruppierte Daten
N
σ2=
∑ (x
i=1
- x)
i
2
1
⋅
N
=
N
1
⋅
N
σ= σ 2 =
N
∑ (x
i
N
∑ (x
- x)
i
2
i=1
- x)
2
i=1
b) Gruppierte Daten
k
∑ (x
σ2 =
- x) ⋅ h i
2
i
i=1
=
N
k
∑  xi*
σ2 =
i =1
k
∑ (x
- x) ⋅ f i
2
i
i=1
2
- x ⋅ hi
N
k
=
∑  xi*
i =1
2
- x ⋅ fi
Die jeweilige Standardabweichung σ ist die (positive) Quadratwurzel der Varianz.
4.4.
Mittlerer Quartilsabstand
MQ =
4.5.
Q3 - Q1
2
Variationskoeffizient
Mit dem Variationskoeffizienten soll die Streuung einer Häufigkeitsverteilung
unabhängig von der absoluten Größe der Merkmalswerte charakterisiert werden. Er
ist ein relatives Streuungsmaß und wird als Quotient aus Standardabweichung und
arithmetischem Mittel berechnet:
V=
σ
x
bzw. V =
σ
x
⋅ 100
7
Statistik I / B. Ziegler
5.
Momente und Schiefe / Konzentrationsmaße
Momente und Schiefe
Das dritte Moment um das arithmetische Mittel wird als Maßzahl für die Schiefe
einer Häufigkeitsverteilung verwendet. Die Schiefe gibt an, wie stark die
Häufigkeitsverteilung von der Symmetrie abweicht.
Das dritte Moment gibt die durchschnittliche dritte Potenz der Abweichungen der
Merkmalswerte vom arithmetischen Mittel an:
a) Ungruppierte Daten
1
⋅
m3 ( x ) =
N
∑ (x i
x) 3
b) Klassifizierte Daten
m3 ( x ) =
Interpretation
m3 ( x ) > 0
m3 ( x ) < 0
6.
k
1 k *
⋅ ∑ ( x − x ) 3 ⋅ h i = ∑ (x*i − x ) 3 ⋅ f i
N i=1 i
i=1
rechtsschiefe Verteilung
linksschiefe Verteilung
Konzentrationsmaße
Konzentrationsmaße messen die Aufteilung einer gesamten Merkmalssumme auf
die einzelnen statistischen Einheiten. In der Konzentrationsmessung werden die
statistischen Einheiten auch als Merkmalsträger bezeichnet.
Je nach Betrachtungsweise wird zwischen absoluter und relativer Konzentration
unterschieden. Der Unterschied besteht darin, daß von absoluter Konzentration
gesprochen wird, wenn ein Großteil der Merkmalssumme auf eine kleine Zahl von
Merkmalsträgern entfällt, von relativer Konzentration, wenn ein Großteil der
Merkmalssumme auf einen kleinen Anteil der Merkmalsträger fällt.
Konzentrationskoeffizient (concentration ratio)
Der Konzentrationskoeffizient (Konzentrationsrate, Konzentrationsziffer oder
Konzentrationsgrad) ist ein weit verbreitetes Maß zur Messung der absoluten
Konzentration.
Gegeben sei eine Anzahl von N Merkmalsträgern (z. B. Unternehmen) mit dem
Merkmal xi (z. B. Umsatz), wobei gilt:
x1 ≤ x 2 ≤ K ≤ x N
8
Statistik I / B. Ziegler
Konzentrationsmaße
Der Konzentrationskoeffizient CRa für a = 2, 3, 4, 5, 6, 10 oder 100 (je nach
Fragestellung) wird definiert als:
N
∑ xi
i = N − a +1
N
CRa =
∑ xi
i =1
Soll beispielsweise der Anteil der drei umsatzstärksten Unternehmen einer Branche
N
oder eines Marktes am Gesamtumsatz ( ∑ xi ) ermittelt werden, so gilt für CR3 bei
i =1
N=10:
10
CR3 =
∑ xi
i =10−3+1
10
∑ xi
i =1
Herfindahl-Index (Hirschman-Index)
Eine weitere Maßzahl der absoluten Konzentration ist der Herfindahl-Index (auch
als Hirschman-Index bezeichnet), der definiert wird als:
N
H = ∑ pi2
i =1
wobei pi = Anteil des Merkmalsträgers i an der gesamten Merkmalssumme.
1
≤ H ≤1
N
Maximale Konzentration liegt dann vor, wenn H = 1 ist (ein Merkmalsträger
vereinigt die gesamte Merkmalssumme auf sich); bei minimaler Konzentration ist
H=
1
N
(alle Merkmalsträger haben den gleichen Anteil an der Merkmalssumme).
9
Statistik I / B. Ziegler
Konzentrationsmaße
Zwischen dem Herfindahl-Index und dem Variationskoeffizienten
(s. Streuungsmaße) besteht folgender Zusammenhang:
H=
(
)
1
⋅ V2 + 1
N
Lorenzkurve und Gini-Koeffizient
Zur Messung der relativen Konzentration wird die Lorenzkurve herangezogen. In
einem quadratischen Schaubild werden auf der Abszisse die kumulierten Anteile
der Merkmalsträger abgetragen, auf der Ordinate die zugehörigen kumulierten
Anteile der Merkmalssumme. Der Streckenzug, der die entsprechenden Punkte –
vom Nullpunkt beginnend – miteinander verbindet, wird als Lorenzkurve
(Konzentrationskurve) bezeichnet.
Der Gini-Koeffizient G ist ein Maß für die Fläche zwischen der Gleichverteilungsgeraden und der Lorenzkurve:
G=
Fläche zwischen der Lorenzkurve und der Gleichverteilungsgeraden
Fläche des Dreiecks unter der Gleichverteilungsgeraden
Zur Berechnung kann folgende Formel verwendet werden:
k
G = 1 − ∑ (MS i −1 + MS i ) ⋅ f i
i =1
mit MS0 = 0
Es gilt: 0 ≤ G ≤ 1.
Bei G = 0 besteht Gleichverteilung, bei G = 1 vollständige Konzentration.
10