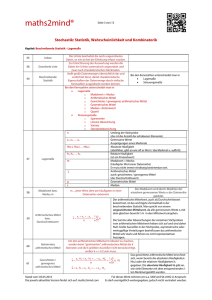
Deskriptive Statistik – Auswertung durch

DeskriptiveStatistik–AuswertungdurchInformationsreduktion
Gliederung
Ø GrundbegriffederDatenerhebung
• Total-/Stichprobenerhebung,qualitatives/quantitativesMerkmal
• EinteilungderDaten(Skalierung,stetiges/diskretesMerkmal,Klassierung)
Ø AuswertungsmethodenfüreindimensionalesDatenmaterial
• Häufigkeitsverteilungen(absolute/relativeHäufigkeiten,Darstellungsformen)
• Lageparameter(Modalwert,Median,arithmetisches/geometrischesMittel)
• Streuungsparameter(Spannweite,Standardabweichung,mittlerequadratische
Abweichung)
• Konzentrationsmaße(Lorenzkurve,Gini-Koeffizient)
2.Kapitel:GrundbegriffederDatenerhebung
TotalerhebungàerfasstGrundgesamtheitvollständig,anderenfallsStrichprobenerhebung
BestandsmassenàMassenderDatenerhebungbeziehensichaufbestimmtenZeitpunkt
BewegungsmassenàbeziehensichaufZeitperiode
QuantitativesMerkmalàMerkmalsausprägungensindZahlen
QualitativesMerkmalàMerkmalsausprägungensindverbaleAusdrücke
àkönnenquantifiziertwerden(AusdruckbekommtZahlzugeordnet)
EinteilungderDatendurchSkalierung
àerfasstwirdSachlogikdernummerischenMerkmalsausprägungen
Nominalskala
Ordinalskala
Kardinalskala
•Merkmalsausprägungen
werdenlediglichdurch
Zuordnung derZahlen
unterschieden (injektive
Abbildung)
•Beispiel:PkwFarbtonzuordnung bei
Herstellung-->grün:117
•Merkmalsausprägungen
könneninRangordnung
gebrachtwerden,welche
Zahlenwiderspiegeln
•Beispiel:Schulnote
•zusätzlichbestimmbar, in
welchemAusmaßsichje2
Merkmalsausprägungen
unterscheiden
•Beispiel:Kopfumfang einer
Person
EinteilungderDatennachMerkmalsart
Klassierung
StetigesMerkmal
DiskretesMerkmal
Behandlungals
quasistetigesMerkmal
BeistetigenMerkmalenkönnenfürzweiMerkmalsaus
prägungenauchalleanderen
Zwischenwerterealisiertwerden.
StetigeMerkmalekönneninKlassen
eingeteiltwerdenàwerdendann
wiediskreteMerkmalebehandelt
Beispiel:ErhebungsbögenfürEinkommen
Ausprägungendiskreter
Merkmalewerdendurch
diskreteZahlenmengen
gebildet.
WenneindiskretesMerkmal
sehrvieleAusprägungenan-
nimmt,behandeltmaneswie
einstetigesMerkmal
Kapitel3.1:Häufigkeitsverteilung
=ZuordnungvonHäufigkeitenzuMerkmalsausprägungena1,…,akausderUrliste;nach
Größegeordnet:a1<a2<…<ak
1) absoluteHäufigkeitvonaj=h(aj);AnzahlderMerkmalswerteinderUrliste,diemit
Ausprägungajübereinstimmen(natürlichepositiveZahl;festerNullpunktundfeste
ganzzahligeEinheiten…Werteabsolut,d.h.unveränderlich)
2) relativeHäufigkeitvonaj=f(aj)=1/n*h(aj);AnteilderElementeeinerMengemit
bestimmterMerkmalsausprägung(Bruchzahlzwischen0bis1)
Darstellungsformen:
a) Häufigkeitstabelle(un-/klassierteDaten)
b) Stabdiagramm(Säulen-)–Koordinatensystem(aj,h(aj)),LotaufAbszisse
(Merkmalsachse)
c) Kreissektorendiagramm–Sektorflächen(unddamitauchdieWinkel)proportionalzu
Häufigkeitenwählen!
d) Histogramm–klassierteDaten,MerkmalsachseinKlassen(Intervalle)einteilen(10
Klassenbeinca.100,13Klassenbeinca.1000,16Klassenbeinca.10.000),
Klassengrenzenäquidistantwählen:HöhederRechteckeproportionalzur
Klassenhäufigkeit
Häufigkeitspolygon–Streckenzug,derdieExtremdatenbzw.Mittenalleroberen
Rechteckseitenverbindet
Kapitel3.2:Lageparameter
Ø KomprimiertDatenmaterialaufeineeinzigeZahlàdamitrepräsentativ,mussWahlauf
geeignetenLageparameterfallen
Modalwert:kennzeichnetAusprägungen,diediegrößteHäufigkeitaufweisen
Median:50%allerMerkmalswertekleiner/50%allerMerkmalswertegrößerodergleich
Quelle:http://www.mathebibel.de/median
ArithmetischesMittel:Durchschnittswert
Quelle:http://www.mathebibel.de/arithmetisches-mittel
àbeiklassiertenDatenàKlassenmitte&relativeKlassenhäufigkeitbeimRechnenverwenden
àwennMerkmalswertez.B.Wachstumsfaktoren,Aufzinsungsfaktoren
àgeometrischesMittel
Quelle:http://www.mathebibel.de/geometrisches-mittel
AusgewählteEigenschaftenvonLageparametern:
1)
Skalierung
nominal
Lageparameter
Modalwert
ordinal
Median
kardinal
arithmetischesMittel
oder
geometrischesMittel
àGegenbeispiel:häufigsteSchuhgröße(eigentlichkardinal)fürProduktionsentscheidung
àErmittlungderModalwerte
2)
Mediangegenüber„Ausreißern“robusteralsarithmetisches/geometrischesMittel
3)(lineareTransformationvonxi)à
4)BeiErrechnungdesarithm.MittelsvondisjunktenMassenMjgilt:
nj:=AnzahlderElementevonMj
n:=Anzahld.ElementGesamtmasseM
(Bamberg,Baur&Krapp,2011,S.18)
5)LageparameterbesitzenOptimalitätseigenschaften
àminimieren(fiktiven/realen)Schaden
Ø arithm./geom.MittelminimiertQuadratsumme
Ø MedianminimiertBetragsumme
Ø ModalwertminimiertSumme
Kapitel3.3:Streuungsparameter
Voraussetzung:kardinalskalierteBeobachtungswertex1,…,xn
a) Spannweite:Differenzzw.kleinstemundgrößtemBeobachtungswert
(„ausreißerempfindlich“)
b) DurchschnittlicheAbweichungvoneinemLageparameter:arithmet.Mitteder
AbständeallerBeobachtungswertevomLageparameter
c) MittlerequadratischeAbweichung:arithmet.MittelderquadriertenAbstände
allerBeobachtungswertevomarithmet.Mittel
d) Standardabweichung:positiveWurzelausdermittlerenquadratischen
Abweichung
e) Variationskoeffizient:QuotientausStandardabweichungundarithmet.Mittel
(maßstabsunabhängig,intuitiv:„Variabilität“,häufigeAngabein%)
Kapitel3.4:Konzentrationsmaße
Ø Offenlegungbzw.VerhinderungvonKonzentrationstendenzen(zeigtUngerechtigkeiten
inderVerteilungauf)
Ø wichtigstesgrafischesMittel:
Lorenzkurve
Ø Punkte(uk,vk)&Punkt(0,0)werdeninKoordinatensystemeingetragen
Ø ukàsummiertenAnteile
o wirderrechnetmituk=k/n(n:=AnzahlderMerkmalsträger)
o Wertfürx-Achse
Ø vkàAnteilederMerkmalssumme
o Wertfüry-Achse
o Zähler:bisherigeSummebiszumk-tenPunkt
Nenner:gesamteMerkmalssumme
Gini–Koeffizient:
Ø stelltInfosausLorenzkurveineinereinzigenZahldar
Ø liegtimIntervall[0,1]
Ø wirdwiefolgterrechnet:
Quelle:http://www.crashkurs-statistik.de/gini-koeffizient/
Ø normierteGini-KoeffizientenG*
o QuotientvonG/Gmax,wobeiGmax=(n-1)/n
o wirdwiefolgterrechnet:
Ø weitereKonzentrationsmaße
o Konzentrationskoeffizient:spiegeltwider,welchenAnteilderMerkmalssummedieggrößtenMerkmalsträgeraufsichvereinigen
o Herfindahl-Index:überdierelativenMerkmalswerte(Klassierung)definierte
Konzentrationsmaß