Feldlinienbild zweier Punktladungen

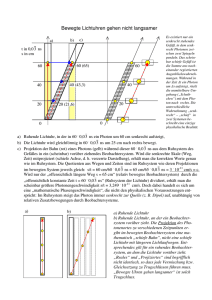
Feldlinienbild zweier Punktladungen
Nebenstehende Abbildung zeigt das
Feld zweier ungleich geladener
Punktladungen QL (links) und QR
(rechts).
a)
Begründen Sie, weshalb es auf
der Verbindungslinie zwischen
den Ladungen keinen Punkt
gibt, in dem die resultierenden
Feldstärke den Wert Null
annimmt.
b)
Warum können sich elektrische
Feldlinien nie schneiden?
c)
Entscheiden und begründen Sie jeweils ob es auf der Verbindungslinie zwischen den
Ladungen Punkte gibt, in denen die resultierende Feldstärke den Wert Null annimmt,
wenn
i)
QL und QR im Vorzeichen und im Betrag übereinstimmen,
ii)
QL und QR im Vorzeichen aber nicht im Betrag übereinstimmen,
iii)
QL und QR weder im Vorzeichen noch im Betrag übereinstimmen.
Die Ladung QL trage dem Betrag nach eine doppelt so große Ladung wie QR .
Zeichnen Sie die entsprechenden Feldlinienbilder, wenn beide Ladungen gleiches
bzw. ungleiches Vorzeichen tragen.
d)
Aufgabenbeispiel: Energie und Potential im homogenen elektrischen Feld
Die folgende Abbildung zeigt fünf äquidistante Äquipotentiallinien im elektrischen Feld eines
Plattenkondensators.
+ 100 V
0
A
B
1
C
2
D
3
4
a) Geben Sie die Potentiale 0 bis 4 an.
Eine negative Probeladung q1 = - 4,0  10-19 C werde im dargestellten elektrischen Feld
verschoben. Geben Sie die Änderung der potentiellen Energie an
b) bei Verschiebung von C nach D;
c) bei Verschiebung von D nach C;
d) bei Verschiebung von A nach B;
e) bei Verschiebung von D nach A;
f) bei Verschiebung von D nach B.
Entscheiden und begründen Sie, ob die Aussage richtig oder falsch ist:
g) Bei Verwendung einer positiven Probeladung q2 = +4,0  10-19 C ändert sich bei den
Ergebnissen von b) bis f) lediglich das Vorzeichen.
h) Bei Verwendung einer positiven Probeladung q2 = +4,0  10-19 C ändert sich bei den
angegebenen Potentialen 0 bis 4 das Vorzeichen.
Feld zweier Punktladungen
In einem Koordinatensystem (1 LE = 1 cm) seien zwei Punktladungen gegeben. Die eine
befinde sich im Punkt L(0 | 0) und trage die Ladung QL  1,0  10 11 C , die andere im Punkt
R(4 | 0) mit einer Ladung von QR  1,0  1011 C . Die Längen im Koordinatensystem
entsprechen den tatsächlichen Längen.
a)
Berechnen Sie die Kraft, die die Ladung QL auf die positive Probeladung
q  1,0  10 13 C in den Punkten A(2/0), B(2/2) und C(4/-4) ausübt. Wiederholen Sie
die Berechnung für die Ladung QR.
b)
Bestimmen Sie mit Hilfe der Pfeiladdition die Kraft und die Richtung die die
Probeladung an den Orten A, B, C erfährt und beurteilen Sie, inwieweit Sie in
Aufgabe a) ihr Feldlinienbild richtig gezeichnet haben. Geben Sie den
Umrechnungsfaktor an, den Sie bei der Erstellung der Kraftpfeile verwendet haben.
Nehmen Sie gegebenenfalls Korrekturen vor.
c)
Nennen Sie weitere Punkte, an denen eine Probeladung denselben Betrag der Kraft
erfährt, wie im Punkt C und zeichnen Sie diese in das Koordinatensystem ein.
Rechtfertigen Sie ihre Entscheidung.
d)
Erstellen Sie ein Feldlinienbild unter Verwendung der bisherigen Informationen.
Vergleichen Sie das Ergebnis mit einer geeigneten Simulation auf einem Rechner.
Äquipotenziallinien
Nebenstehende Abbildung zeigt den
Feldlinienverlauf zweier Punktladungen.
a)
Entscheiden Sie, ob es sich um zwei
gleichnamige oder ungleichnamige
Ladungen handelt und tragen Sie die
Vorzeichenverteilung der Ladungen
ein. Beachten Sie die Richtung der
Feldlinien.
b)
Geben Sie verschiedene Kriterien an,
denen Äquipotentiallinien bei
gegebenem Feldlinienverlauf gerecht
werden müssen.
c)
Tragen Sie den Verlauf der Äquipotentiallinien in die nebenstehende Zeichnung ein.
Globaler elektrischer Kreislauf in der Atmosphäre (aus Grundkursabitur 2009,
modifiziert)
Man stellt sich vor, dass in der
Atmosphäre ein globaler elektrischer
Kreislauf
existiert.
Die
Ladungstrennung in den Wolken bildet
die „Batterie“ dieses Stromkreises.
Durch diese Ladungstrennung wird die
sogenannte mittlere Atmosphäre, eine
Schicht in rund 40 km Höhe, positiv
aufgeladen,
so
dass
zwischen
mittlerer Atmosphäre und Erdboden
eine Spannung von U = 400 kV
herrscht.
Sowohl
die
mittlere
Atmosphäre als auch der Erdboden können als leitend angesehen werden. In
Schönwetterregionen bilden positiv geladene Ionen einen ständigen Stromfluss von der
Atmosphäre zum Erdboden, in Gewitterregionen wird durch Blitze der Stromkreis
geschlossen. Die weltweit beobachtbaren Ströme in Schönwetterregionen können zu einem
Gesamtstrom der Stärke I = 1,3 kA zusammengefasst werden. Ohne anhaltende
Ladungstrennung wäre bei Annahme eines konstanten Stromes I die mittlere Atmosphäre
nach 14 Minuten entladen.
a)
Berechnen Sie die Gesamtladung Q der mittleren Atmosphäre.
[zur Kontrolle: Q  1,1  10 6 C ]
b)
Trotz des Stroms kann man die Schönwetterregion als Kondensator mit der mittleren
Atmosphäre und dem Erdboden als Kondensatorplatten auffassen. Berechnen Sie
unter Annahme eines homogenen elektrischen Felds den Betrag der Kraft Fel auf ein
einfach positiv geladenes Ion in der Schönwetterregion.
c)
Zeigen Sie durch eine Abschätzung, dass der Betrag der Energie, die im elektrischen
Feld der Schönwetterregion gespeichert ist, in der Größenordnung 10 11 J liegt.
d)
Nehmen Sie an, man könnte diese Energie in einem Kraftwerk im Dauerbetrieb
nutzbar machen. Welche Leistung hätte das Kraftwerk? Wäre es sinnvoll, diese
Ressource als „Energiequelle der Zukunft“ zu nutzen? Begründung!
e)
Ein Normblitz transportiert in etwa eine Ladung von 70 C. Berechnen Sie, wie viele
Normblitze es durchschnittlich pro Sekunde weltweit geben muss, damit der globale
Kreislauf aufrecht erhalten werden kann.
f)
Schätzen Sie ab, wie lange ein Blitz dauert, wenn der Entladestrom im Mittel 140 kA
beträgt.
Arbeitsblatt zur quantitativen Bestimmung der Zeitdilatation am Beispiel der bewegten
Lichtuhr
Während in der Newton’schen Mechanik die Zeit eine absolute Größe darstellt und in allen
Systemen in gleicher Weise dahinfließt, ist dies bei der Einstein’schen Relativitätstheorie
nicht der Fall. Dort gelten die beiden bereits bekannten Postulate, die experimentell vielfach
untermauert sind:
1. Alle Inertialsysteme (unbeschleunigte Bezugssysteme) sind gleichberechtigt, d. h. die
physikalischen Gesetze haben in allen Inertialsystemen exakt die gleiche Form. (Ein
Inertialsystem ist beispielsweise eine durch den Weltraum schwebende Rakete mit
ausgeschalteten Triebwerken, doch auch die Erdoberfläche oder ein mit konstanter
Geschwindigkeit fahrender Zug können näherungsweise als Inertialsysteme betrachtet
werden, solange man nicht die vertikale Bewegungsrichtung betrachtet)
2. Die Lichtgeschwindigkeit c hat in allen Inertialsystemen exakt den gleichen Wert
c = 300 000 km/s (genauer Wert c = 299792458 m/s).
Dies hat einige erstaunliche – ebenfalls bereits bekannte – Konsequenzen. So registriert ein
Beobachter, dass in einem relativ zu ihm bewegten Bezugssystem die Zeit langsamer
vergeht. Beispielsweise misst ein Beobachter B’ in einem schnellen Zug für einen Vorgang
dort eine kleinere Zeit, als der - sich am Bahnsteig befindende - Beobachter B dafür ermittelt.
Dies kann man dem Modell einer Lichtuhr nachvollziehen:
Eine Lichtuhr (ein zylindrisches
Gefäß, an dessen Boden Licht
ausgesandt wird und an dessen
Deckel die Ankunft des Lichts
registriert wird; die dazu benötigte
Zeit wird gemessen) der Höhe h
befinde sich in einem Zug, der sich
mit konstanter Geschwindigkeit v
bewegt.
Aus
Sicht
eines
mitreisenden
Beobachters
B’
wandert das Licht senkrecht nach
oben. Der mitbewegte Beobachter
B’ misst die Zeitspanne t’, die das
Licht benötigt, um vom unteren
Ende der Lichtuhr zum oberen zu
gelangen.
B’
B’
h
v
l
B
Aufgabe 1:
Begründen Sie, dass für B’ gilt h = c t’ (I) und berechnen Sie, wie lange es aus Sicht des
mitbewegten Beobachters B’ dauert, bis das Licht eine Lichtuhr der Höhe h = 300,0 m
durchläuft.
(zur Kontrolle t’ = 1,000 µs)
Ein am Bahnsteig stehender Beobachter B, der die Lichtuhr im Zug mit der Geschwindigkeit
v an sich vorbeisausen sieht, beobachtet, wie das Licht entlang der Hypotenuse s eines
rechtwinkligen Dreiecks wandert. Denn während sich das Licht nach oben bewegt, fährt der
Zug um die Strecke l = v t (II) weiter, wenn t aus seiner Sicht das Zeitintervall ist, welches
das Licht benötigt, um vom unteren zum oberen Ende der Lichtuhr zu gelangen.
Aufgabe 2:
Begründen Sie, dass für B der Zusammenhang s = c t (III) gilt und leiten Sie daraus die
Bedingung
1
t 
t  (IV)
 v2 
1  2 
 c 
her.
Hinweis: Berechnen Sie zuerst die Hypothenuse s des rechtwinkligen Dreiecks mit Hilfe des
Satzes von Pythagoras. Setzen Sie das Ergebnis in (III) ein.
Aufgabe 3
Die Formel (IV) besagt, dass Beobachter B’ für denselben Prozess in seinem Zug eine
kleinere Zeit misst, als Beobachter B, der den Prozess vom Bahnsteig aus betrachtet.
Diskutieren Sie, wie man zu dieser Aussage kommt.
Relativistische Effekte zeigen sich nur bei sehr hohen Geschwindigkeiten. Nehmen Sie
deshalb für die nächste Aufgabe an, dass der Zug sehr schnell mit v = 40 000 km/s (also
eine Erdumrundung pro Sekunde) fährt.
Aufgabe 4
Zeigen Sie, dass für den am Bahnsteig ruhenden Beobachter B das Licht vom Boden zum
Deckel der Lichtuhr nicht 1,000 µs, sondern 1,009 µs benötigt. Begründen Sie warum B mit
Fug und Recht behaupten kann: „Die bewegte Uhr im Zug geht langsamer“.
Aufgabe 5
Welche bemerkenswerten Konsequenzen haben Ihre Ergebnisse im Bezug auf den Begriff
der Gleichzeitigkeit? Diskutieren Sie den Fall, dass sich B und B’ darüber einig sind, dass
das Licht zum gleichen Zeitpunkt das untere Ende der Lichtuhr verlässt.
Aufgabe 6
Nehmen Sie nun an, dass auch der Beobachter B am Bahnsteig eine Lichtuhr aufgebaut hat
und diskutieren Sie die Frage, für welchen Beobachter diese Uhr nun langsamer geht.
Bedenken Sie dabei, dass man Zug und Bahnsteig gleichermaßen als Inertialsysteme
betrachten kann. Informieren Sie sich im Schulbuch oder im Netz über das
Zwillingsparadoxon.
Lebensdauer von Myonen
Myonen entstehen in ca. 10 km Höhe durch Reaktionen der kosmischen Strahlung mit Atomkernen
und Molekülen der Atmosphäre. Ruhende Myonen haben eine mittlere Lebensdauer von ca.
  2, 2 s und eine Geschwindigkeit von ca. v  0,9998c .
a)
b)
c)
d)
Berechnen Sie klassisch, wie weit ein Myon fliegen kann, bevor es im Mittel
zerfällt.Tatsächlich können Myonen auf der Erdoberfläche nachgewiesen werden. Dieses
Ergebnis steht im Widerspruch zu a). Dieser kann aber mit einer relativistischen Betrachtung
des Problems aufgelöst werden.
Ein Beobachter B’ fliege mit den Myonen Richtung Erde mit. In seinem Bezugssystem ruhen
die Myonen und er misst daher eine mittlere Lebensdauer von  '  2, 2s . Für einen
Beobachter B auf der Erde bewegt sich B’ aber mit sehr hoher Geschwindigkeit. B sieht, wie
die Uhr von B’ eine Zeit von 2, 2 s anzeigt. Berechnen Sie die Zeit, die demnach Beobachter
B für die mittlere Lebensdauer der Myonen gemessen hat.
Berechnen Sie nun, welche Strecke ein Myon innerhalb seiner mittleren Lebensdauer aus
Sicht von B zurücklegen kann. Kann es die Erdeoberfläche erreichen?
Auch aus der Sicht von B’ erreichen die Myonen die Erdoberfläche! Wie sieht seine Rechnung
aus?
Ringbeschleuniger HERA
Im Ringbeschleuniger HERA (Hadron-Elektron-Ring-Anlage) werden Protonen beschleunigt,
bis sie eine kinetische Energie von ca. 900 GeV besitzen.
a)
Berechnen Sie die Geschwindigkeit dieser Elektronen mit der bekannten Formel
m
Ekin  v 2 . Nehmen Sie Stellung zu ihrem Ergebnis. Wie lässt sich der vermeintliche
2
Widerspruch auflösen?
b)
Berechnen Sie die Masse, die ein Elektron mit oben genannter Energie besitzt.
c)
Ermitteln Sie die tatsächliche Geschwindigkeit dieser Elektronen.