Prof
Werbung

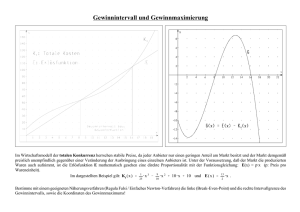
Prof. Dr. Rainer Marggraf WS 2007/08 Vorlesung Volkswirtschaftslehre Übungsfragen 11. Kostenminimierung 11.1 Nadine verkauft benutzerfreundliche Software. Die Produktionsfunktion ihres Unternehmens lautet f(x1, x2) = x1 + 2x2, wobei x1 die Menge an ungelernter Arbeit und x2 die Menge an gelernter Arbeit ist, die sie beschäftigt. a) Zeichnen Sie eine Produktionsisoquante, die jene Inputkombinationen zeigt, die 20 Outputeinheiten erzeugen. – Zeichnen Sie noch eine Isoquante, die Inputkombinationen darstellt, die 40 Outputeinheiten erzeugen. b) Wenn Nadine nur ungelernte Arbeiter einsetzte, wie viele ungelernte Arbeiter würde sie dann brauchen, um y Outputeinheiten zu erzeugen? c) Wenn Nadine nur gelernte Arbeiter einsetzte, wie viele gelernte Arbeiter würde sie dann brauchen, um y Outputeinheiten zu erzeugen? d) Wie kann Nadine 20 Outputeinheiten am billigsten herstellen, wenn sie sich den Faktorpreisen (1, 1) gegenübersieht? x1 = ........................., x2 =............................. e) Wie kann Nadine 20 Outputeinheiten am billigsten herstellen, wenn sie sich den Faktorpreisen (1, 3) gegenübersieht? x1 = ........................., x2 =............................. 11.2 Ein Unternehmen verwendet Arbeit und Maschinen, um einen Output gemäß der Produktionsfunktion f(L, M) = 4L1/2M1/2 zu erzeugen, wobei L die Zahl der verwendeten Arbeitseinheiten und M die Zahl der eingesetzten Maschinen ist. Arbeit kostet € 40 je Einheit, die Kosten des Einsatzes einer Maschine sind € 10. a) Zeichnen Sie zwei Isokostenlinien für dieses Unternehmen, welche jene Kombinationen von Arbeit und Maschinen abbilden, die einmal Gesamtkosten von € 200 und ein andermal Gesamtkosten € 400 verursachen. Wie groß ist die Steigung dieser beiden Isokostengeraden? b) Angenommen das Unternehmen möchte seinen Output so billig wie möglich erzeugen. Suchen Sie die Anzahl an Maschinen, die es je Arbeiter einsetzen würde. 11.3 Die Mensa einer Universität bereitet eigenartige Mahlzeiten mit nur einem Input zu. Die Produktionsfunktion der Mensa lautet f(x) = x2, wobei x die verwendete Inputmenge und f(x) die Anzahl der erzeugten Mahlzeiten darstellen. a) Wie viele Inputeinheiten benötigt man zur Herstellung von 144 Mahlzeiten? – Wie hoch sind die Kosten der 144 Mahlzeiten, wenn der Input je Einheit w kostet? b) Wie viele Inputeinheiten benötigt man zur Herstellung von y Mahlzeiten? – Wie hoch sind die Kosten von y Mahlzeiten, wenn der Input je Einheit w kostet? c) Wie hoch sind die Durchschnittskosten von y Mahlzeiten, wenn der Input je Einheit w kostet? AC(w, y) = ............................................ 12. Kostenkurven 12.1 Herr Otto Karr, der Besitzer von Ottos Autos, verkauft Autos. Otto kauft Autos für € c je Stück, er hat keine anderen Kosten. a) Wie hoch sind seine Gesamtkosten, wenn er 10 Autos verkauft? – Wenn er 20 Autos verkauft? – Schreiben Sie die Gleichung für Ottos Gesamtkosten unter der Annahme an, daß er y Autos verkauft: TC(y) = .................................................. b) Wie lautet Ottos Durchschnittskostenfunktion? AC(y) = ............................................. Für jedes zusätzliche Auto, das er verkauft, steigen seine Kosten um ....................... Schreiben Sie Ottos Grenzkostenfunktion an: MC(y) = .............................................. c) Zeichnen Sie in eine Grafik Ottos Durchschnitts- und Grenzkostenkurven für c = 20 ein. d) Angenommen Otto muß € b pro Jahr für die Produktion von abscheulichen FernsehWerbefilmen zahlen. Ottos Gesamtkostenkurve lautet nun: TC(y) = .........................., seine Durchschnittskostenkurve ist AC(y) = ............................................ und seine Grenzkostenkurve ist MC(y) = .................................................. e) Zeichnen Sie Ottos Durchschnittskostenkurve für b = € 100 in die Grafik ein. 12.2 Ottos Bruder, Karl Karr, repariert Autos. In jüngster Zeit hatte Karl wenig zu tun, er entschloß sich daher zu einer Analyse seiner Kostensituation. Es stellte sich heraus, daß die Gesamtkosten für die Reparatur von s Autos TC(s) = 2s2 + 10 sind. Dann wurde Karl jedoch von seiner Kostenanalyse wieder abgelenkt ... und jetzt sind Sie dran. Vervollständigen Sie bitte: a) Karls gesamte variable Kosten: .................................................................... b) Gesamte Fixkosten: ....................................................................................... c) Durchschnittliche variable Kosten: ................................................................ d) Durchschnittliche Fixkosten: ........................................................................... e) Grenzkosten: .................................................................................................... 12.3 Ein dritter Bruder, Rex Karr, besitzt einen Schrottplatz. Rex kennt nur zwei Arten, um Autos zu zerstören. Erstens kann er eine hydraulische Presse kaufen, die pro Jahr € 200 kostet, er muß dann für jedes zerstörte Auto € 1 aufwenden; zweitens könnte er einen Bagger um € 10 pro Jahr kaufen und dann dem letzten der Karr-Brüder, Schippe, € 5 für das Einbaggern eines Autos zahlen. a) Schreiben Sie die Gesamtkostenfunktionen beider Methoden an, wobei y der Output pro Jahr ist: TC1(y) = .................................... und TC2(y) = .................................... b) Die erste Methode hat die Durchschnittskostenfunktion AC1(y) = ............................. und die Grenzkostenfunktion ist MC1(y) = ......................................, für die zweite Methode sind diese Funktionen AC2(y) = ...................... und MC2(y) = ...................... c) Welche Methode sollte Rex verwenden, wenn er pro Jahr 40 Autos abwrackt? – Und wenn er 50 Autos abwrackt? – Ab welcher Zahl von Autos lohnt es sich für Rex, die hydraulische Presse zu kaufen?