Lineare Funktionen

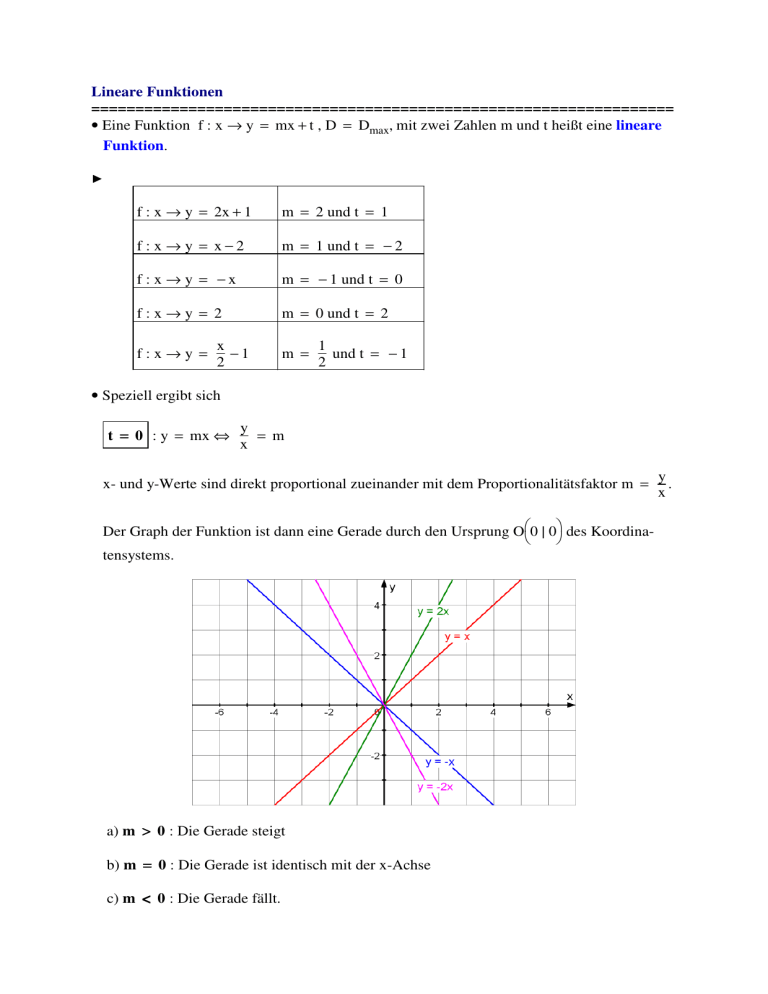
Lineare Funktionen
==================================================================
• Eine Funktion f : x → y = mx + t , D = Dmax, mit zwei Zahlen m und t heißt eine lineare
Funktion.
²
f : x → y = 2x + 1
m = 2 und t = 1
f: x → y = x−2
m = 1 und t = − 2
f : x → y = −x
m = − 1 und t = 0
f:x→y = 2
m = 0 und t = 2
f:x→y =
x
−1
2
m =
1
und t = − 1
2
• Speziell ergibt sich
t = 0 : y = mx ⇔
y
= m
x
x- und y-Werte sind direkt proportional zueinander mit dem Proportionalitätsfaktor m =
Der Graph der Funktion ist dann eine Gerade durch den Ursprung O0 | 0 des Koordina

tensystems.
a) m > 0 : Die Gerade steigt
b) m = 0 : Die Gerade ist identisch mit der x-Achse
c) m < 0 : Die Gerade fällt.
y
.
x
m heißt auch Steigungsfaktor der Geraden.
t≠0
Der Graph der Funktion f : x → y = mx + t
ist dann eine zum Graphen der Funktion f : x → y = mx
parallele Gerade durch den Punkt Sy0 | t
 
²
• heißt y-Abschnitt der Geraden.
• Den Steigungsfaktor m einer Geraden kann man mit Hilfe eines Steigungsdreiecks dem
Schaubild der Geraden entnehmen
Bb1 | b2


b2 − a2
Aa1 | a2


b1 − a1
Sind Aa1 | a2 und Bb1 | b2 die auf der Gerade liegenden Eckpunkte des Steigungsdrei



ecks, dann ist
m =
b 2 − a2
∆y
=
∆x
b 1 − a1
∆y = b2 − a2 ist gleich der Zu- oder Abnahme der y-Werte bei einer Zunahme oder Abnahme der x-Werte um ∆x = b1 − a1.
² Für die Gleichung der Geraden durch die Punkte A1 | − 2 und B4 | 2 ergibt sich




m =
4
4
. Also hat Gleichung der Geraden die Form y = x + t.
3
3
Da der Punkt A auf der Geraden liegt, muss sich beim Einsetzen der x-Koordinate des
Punktes seine y-Koordinate ergeben. Also
−2 =
4
⋅1 + t
3
⇒
t = −
10
3
10
4
x−
3
3
___________________________________________________________________________
und damit ergibt sich für die Gerade AB die Gleichung y =
Aufgaben
___________________________________________________________________________
1. Bestimme die Funktionsgleichung einer linearen Funktion mit der Wertetabelle
a)
x
y
−3
2
5
4
b)
x
y
−3
7
2
−3
12
x
−7
13
13
y
-----------------------------------------------------------------------------------------------------------------2. Bestimme die Funktionsgleichung einer linearen Funktion deren Graph
c)
a) durch die 2 Punkte P1 | 1 und Q − 3 | 6 geht.




b) durch die 2 Punkte P − 12 | − 12 und Q0 | 12.




c) den y-Abschnitt t = 2 hat und durch den Punkt P7 | 4 geht.


d) die Steigung m = 2 hat durch den Punkt P − 2 | 5 geht.


-----------------------------------------------------------------------------------------------------------------3. Bestimme die Nullstellen der folgenden linearen Funktionen
1
3
b) f : x → y = − 2x
1
x−5
5
d) f : x → y = − 1
a) f : x → y = 3x −
c) f : x → y = −
2
2
1
x+
e) f : x → − x +
5
3
2
-----------------------------------------------------------------------------------------------------------------4. Bestimme graphisch und rechnerisch die Koordinaten des Schnittpunkts der Graphen der
beiden Funktionen
d) f : x → y =
a) f1 : x → y = −
3
1
x + 3 und f2 : x = x − 2
4
2
4
2
x + 3 und f2 : x = x + 1
9
3
-----------------------------------------------------------------------------------------------------------------b) f1 : x → y =
5.Die Punkte ( − 16) und B(63) sind Elemente der Geraden g. Die Gerade h geht durch den
3
Punkt C(12) und hat die Steigung .
4
a) Ermittle graphisch die Koordinaten des Schnittpunktes S von g und h !
b) Stelle die Gleichungen von g und h auf und berechne die Koordinaten von S !
-----------------------------------------------------------------------------------------------------------------6.Gib die Funktionsgleichungen der Geraden g und h an
und berechne die Koordinaten ihres Schnittpunktes S !
-----------------------------------------------------------------------------------------------------------------12
7
7 Wie lautet die Gleichung der Parallelen zu y = x −
durch den Punkt (18 − 23) ?
3
5
----------------------------------------------------------------------------------------------------------------8 Untersuche rechnerisch, ob die drei Punkte A( − 64), B(5 − 3) und C( − 75,5) auf einer
Geraden liegen.
-----------------------------------------------------------------------------------------------------------------9 Die Punkte P(42), Q(1v), R(u13) liegen auf einer Geraden.
Wie groß sind u und v ?
-----------------------------------------------------------------------------------------------------------------10. Bestimme die Gleichungen der eingezeichneten
Geraden.
___________________________________________________________________________