Vorwort

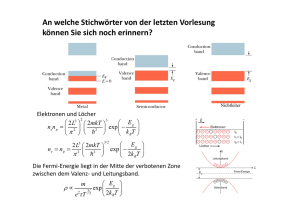
75900629
166
5/14/2016
Die atomaren Potentiale, die in der Figur eingezeichnet sind (grünen Linien) zeigen den
Fall starker Überlappung. Die Summe der Atom-Potentiale ist durch die blauen Linien
dargestellt. Im Fall von Überlappung sind  n (r) keine Eigenfunktionen mehr. Zum
Hamiltonoperator Hˆ (r) für das ungestörte Atom bei r  0 muss ein Störpotential
at
U (r ) addiert werden, das durch die periodische Anordnung aller Atome erzeugt wird
Hˆ cr (r)  Hˆ at (r)  U (r)
(rote Linien in Figur) und etwas verschieden sein kann von der simplen Addition der
Atompotentiale Vat (r  R) . Trivialerweise gilt, dass die atomaren Wellenfunktionen
 (r) überall dort die Schrödingergleichung mit Hˆ (r) erfüllen, wo U (r )
n
cr
verschwindet. Als Lösung für Hˆ cr (r) setzen wir deshalb eine Linearkombination von
Wellenfunktionen an
nk (r )   c kR n (r  R ) .
R
Da Hˆ cr (r) periodisch ist, müssen nk (r ) Blochwellen sein, das heisst
nk (r  R )  nk (r )e ik R .
Man kann zeigen (Ashcroft and Mermin, p. 178), dass
nk (r )   e ik R n (r  R)
R
eine Lösung von Hˆ cr (r) ist. Aufgrund der periodischen Randbedingungen kann die
Wellenzahl k in der 1. Brillouinzone N Werte annehmen.
In einer 1. Näherung nehmen wir an, dass überall dort, wo das Potential nicht Null ist, die
Wellenfunktion nk (r ) genügend klein ist, damit man Störungstheorie 1. Ordnung
anwenden kann. Aufgrund des Störpotentials U (r ) werden die Wellenfunktionen n (r )
durch neue Funktionen  kn (r ) ersetzt und man erhält
 nk (r )   bn n (r  R ) .
R
Für die Energieniveaus erhält man durch Einsetzen der 0ten-Näherung nk (r ) in 1.
Näherung für die Energieeigenwerte die Gleichung
Hˆ cr (r)nk (r)  ( Hˆ at (r)  U (r))nk (r)  En (k )nk (r) .
75900629
167
5/14/2016
Durch Multiplikation von links mit dem Atomorbital  n* (r ) und Integration über das
Grundgebiet erhält man

*
n
Hˆ nk dr   n*Unk dr  En (k ) n* nk (k )dr .
at
Für das 1. Integral ergibt sich
A   n* Hˆ nk dr  E nat  n* nk dr  E nat  n* (r ) e ik R n (r  R ) .
at
R
Daraus folgt


ik R
A  E nat 1   e ik R  n* (r ) n (r  R)dr   E nat (1   e  (R)) .
R 0
 R 0

Für das 2. Integral findet man
B   n* (r)U (r) n (r)dr   e
ik R
R 0

*
n
(r)U (r) n (r  R)dr      e ikR (R) .
R 0
Für das 3. Integral folgt trivialerweise
C  En (k ) e
ik R
R

C  E n (k )(1   e
*
n
ik R
(r) n (r  R)dr  En (k )(1   e ikR  n* (r) n (r  R))
R 0
 (R))
R 0
Zusammengenommen gilt A  B  C und man erhält für die Energiedispersion die
Funktion
E n (k )  E nat 
   e ik  R  ( R )
R 0
1   e ik  R  ( R )
.
R 0
Mit den Abkürzungen für die Integrale:
 (R )   n* (r ) n (r  R )dr ,

   n* (r )U (r ) n (r )dr
 (R )    n* (r )U (r ) n (r  R )dr .
(  ist unabhängig von R),
75900629
168
5/14/2016
Schwache Überlappung: Das Überlappintegral  (R ) ist <<1 für nächste Nachbarn. Für
weiter entfernte Nachbarn ist  (R ) völlig vernachlässigbar, da die Wellenfunktionen
exponentiell abnehmen. Deshalb kann man den Nenner vernachlässigen und man erhält
E n (k )  E nat     e ik R  (R) ,
NN
wobei NN = nächste Nachbarn bedeutet. Wenn die Gitterperiode a   geht, geht
E n (k )  E nat . Da nur der letzte Term von k abhängt, wird die Breite des Energiebandes
umso grösser, je stärker die Orbitale benachbarter Atome überlappen.
Beispiel: s-Band eines kfz-Gitters:
Die 12 nächsten Nachbarn sind an den Positionen a2 (1,1,0) a2 (0,1,1) a2 (1,0,1) . Da
die s-Funktionen kugelsymmetrisch sind (hängen nur von r ab), sind die Integrale  und
 für jedes benachbarte Atom äquivalent, sodas man  (R)   0 setzen kann. Damit
erhält man für die Energie

E n (k )  E n    4 0 cos( 12 k x a) cos( 12 k y a)  cos( 12 k y a) cos( 12 k z a)  cos( 12 k z a) cos( 12 k x a)
,
wobei a die Kante der flächenzentrierten Elementarzelle bedeutet. Für eine Diskussion
dieser Bänder siehe Übungsserie 20, Aufgabe 1.
Aufgrund der Tatsache, dass der Kristall stabil ist, muss U (r )  0 sein. Damit sind die
Konstanten  und  0 positiv, was einer Erniedrigung der Energie E n (k ) in Bezug auf
En entspricht. Man sieht sofort, dass mit zunehmendem Überlapp die Bandbreite W
zunimmt: W  16 0 entlang [100] und W  12 0 entlang [111].
Die Berechnung von p-Bändern ist wegen der (2l  1) - fachen Entartung der Bänder
bezüglich der Quantenzahl l viel schwieriger. Siehe zum Beispiel “Electronic Structure
and the Properties of Solids” by Walter A. Harrison (1979).

75900629
169
5/14/2016
5. Halbleiter
Halbleiter sind Festkörper mit einem Bandgap der Grössenordnung 1 eV. Die elektrische
Leitfähigkeit bei 300 K liegt zwischen denen eines Metalls und eines Isolators:
10 12    1  -1cm -1 . Sie kann durch geziehlte Zugabe von Fremdatomen (Dotierung)
über viele Grössenordnungen variiert werden.
Beispiele:
Ge, Si, GaAs, AlGaAs, GaP, GaN, InSb, InP, ZnSe, Polyazetylen
Fast alle Halbleiterbauelemente bestehen aus Silizium. Si wird aus Quarzsand und Kohle
hergestellt:
1. SiO2+2CSi+2CO:
Reinheit ca. 98%
2. Destillation mit
Trichlorsilanprozess:
Si+3Cl+HSiHCl3
SiHCl3+H2Si+3HCl
(Rohsilizium)
3. Czochralski-Ziehverfahren: ca. 10
cm/Stunde
Grösse der gezogenen Kristalle: 2 m lang,
bis 30 cm Durchmesser (Wacker,
Burghausen). Si hat Diamantstruktur mit
der Gitterkonstanten a  5.431 Å.
Für Ge ( a  5.658 Å ) wird ein ähnliches
Herstellungsverfahren verwendet. Der
erste Transistor wurde mit Ge gebaut.
Weitere Anwendungen von Halbleitern:



Optoelektronik: III-V Halbleiter
wie GaAs ( a  5.654 Å ) and
AlGaAs
Laser: InP, InGaAsP (   1.55 Å)
Blaue Leuchtdioden: ZnSe
75900629
170
5/14/2016
5.1. Bandstruktur
Wir haben bereits einige Aspekte der Bandstruktur von Ge, Si und GaAs im
Zusammenhang mit optischen (direkten/indirekten) Übergängen und Fermiflächen
(Zyklotronresonanz) diskutiert. Pro Elementarzelle sind zwei Atome vorhanden. Die vier
Valenzbänder sind voll besetzt mit 4 (Si: 3s23p2, Ge: 4s24p2) beziehungsweise 3 + 5
(GaAs) Elektronen. Die Bandbreite der Valenzelektronen in Si beträgt ca. 12 eV und die
indirekte Bandlücke ca. 1.1 V.
schwere
Löcher

Split-off
Band
leichte
Löcher
schwere
Löcher
Valenzbänder
W = 12 eV
leichte
Löcher
L

[111]
X
[100]
Wichtig für die elektronischen Eigenschaften sind die Zustandsdichten und Massen an
den Bandkanten. In deren Nähe kann die Dispersionsrelation durch Parabolas angenähert
werden:

Löcher:

Elektronen:
 k x2 k y2 k z2 




 m* m* m* 
y
z 
 x
2
2  k 2 ky k 2 
E L (k )  E L   x*  *  z*  .
2  m x m y m z 
2
EV (k )  EV 
2
Die Massen sind hier als positive Grössen definiert.
75900629
171
5/14/2016
Im Beispiel von Si hat man:

leichte Löcher: grosse Krümmung: pp-Bindung; starke, bindende
Wechselwirkung  grosse Bandbreite

schwere Löcher: kleine Krümmung: pp-Bindung; schwächere Wechselwirkung

split-off Band: entsteht aus dem Band schwerer Löcher wegen der Spin-Bahn
Kopplung,  hängt von der Stärke der Kopplung ab. Merke: p-Bänder haben
l  1 . Je grösser die Kernladungszahl Z ist, desto grösser  (in Si: 44 meV, in
Ge: 290 meV):   Z 2 . In Si sind das schwere Löcher Band und das splitt-off
Band kaum unterscheidbar.
L
+Ze

Kreisstrom
erzeugt durch e-
Elektronen im Leitungsband: Wir haben gesehen, dass die Fermifläche durch
sechs Ellipsoide gegeben ist, die für die relevanten Zustände innerhalb der 1.
Brillouinzone liegt. Das Minimum liegt nicht beim -Punkt.
In der folgenden Diskussion gehen wir von isotropen, effektiven Massen und setzen
m*  (m*x m*y m*z )1 / 3 . Wir vernachlässigen auch das Vorhandensein mehrerer Bänder.
5.2. Eigenhalbleiter (intrinsic semiconductor)
In der folgenden Figur sind die relevanten Energien zur Berechnung der
Ladungsträgerkonzentration eingezeichnet. Wir haben willkürlich die Oberkante des
Valenzbands als Energienullpunkt EL  0 gewählt. Es ist üblich, auf der Abszisse
symbolisiert den Ort der Ladungsträger (= Wellenpaket) anzudeuten.
75900629
172
5/14/2016
E
EL
Eg
EF
EV
0
x
Für die Eigenwertdichte im Leitungsband erhält man:
 2me* 


 L (E) 
(2 ) 2   2 
1
3/ 2
E  EL .
Die Fermifunktion ist gegeben durch
1
Fe ( E ) 
e
E 
k BT
.
1
Die Eigenwertdichte im Valenzband ist gegeben durch:
 2me* 


V ( E ) 
(2 ) 2   2 
1
3/ 2
EV  E .
Die Fermifunktion für die Löcher lautet (Wahrscheinlichkeit für “kein” Elektron)
1
F p ( E )  1  Fe ( E )  1 
e
E 
k BT
1

1
.
 E
e
k BT
1
Somit erhalten wir für die Anzahl der Leitungselektronen pro Volumeneinheit
 2me* 


n
(2 ) 2   2 
2
2/3 

E  Eg
Eg
1
e
( E   ) / k BT
1
dE
und für die Löcher
 2m*p 


p
(2 ) 2   2 
2
2/3
0


E
1
e
(   E ) / k BT
1
dE .
75900629
173
5/14/2016
Die folgende Figur zeigt  i (E ) , Fi (E ) und die Verteilungsfunktion (violet) für
Elektronen und Löcher bei endlicher Temperatur.
2.0
Besetzungswahrscheinlichkeiten
Zustandsdichten
1.5
e(E)
F(E), ()
p(E)
1.0
Fe(E)
Fp(E)
0.5
0.0
EV
EL
File Halbleiter.opj
Energy
Da bei Raumtemperatur die Bandlücke E g  k B T ist, kann die 1 im Nenner der
Fermifunktion vernachlässigt werden ( Boltzmannfunktion) und man erhält für die
Anzahl der Ladungsträger
 2me* 


n
(2 ) 2   2 
2
3/ 2 

E  Eg e
(   E ) / k BT
Eg
 m*k T 
dE  2 e B2 
 2 
3/ 2
e
(   E g ) / k BT
und
 2m*p 


p
(2 ) 2   2 
2
3/ 2


 Ee
( E   ) / k BT
Eg
 m*p k BT 

dE  2
 2 2 


3/ 2
e   / k BT .
Für einen perfekt reinen Kristall stammen alle Elektronen im Leitungsband aus dem
Valenzband, i.e. der Kristall ist neutral. Also muss gelten
n p.
.
Daraus folgt:
n  me* 
1 
p  m*p 
3/ 2
e
( 2   E g ) / k BT


Eg
2

m*
3
k BT ln *p .
4
me
75900629
174
5/14/2016
E
EL
me < mp
me = mp
me < mp
EV
Eg
EF
0
T
Für gleiche Massen liegt E F in der Mitte zwischen Valenz- und Leitungsband. Sonst
wird E F bei endlicher Temperatur in Richtung des Bands mit der leichteren Masse
verschoben. Vergleiche dieses Verhalten mit dem Gas von entarteten Teilchen bei dem
E F , oder genauer  , mit zunehmender Temperatur abnimmt. Beachte, dass in der
Diskussion von Halbleitern oft nicht zwischen dem chemischen Potential  und E F
unterschieden wird.
 m* k T 
Weiter erhalten wir mit N e  2 e B2 
 2 
3/ 2
 m *p k BT 

und N p  2
 2 2 


3/ 2
3
n  np  4(m m )
2
i
*
e
* 3/ 2
p
 k BT   Eg /(k BT )
 N e N p e ( EL  EV ) / k BT .

 e
2
 2 
Dieser Ausdruck entspricht dem Massenwirkungsgesetz. ni nennt man die intrinsische
Ladungsträgerdichte. Zusammen mit ni  n  p folgt hieraus für die Konzentration der
Ladungsträger des Eigenhalbleiters (RT: N eSi  2.8  1019 cm 3 , N pSi  1.04  1019 cm 3 )
ni  n  p  N e N p e
 E g /( 2 k BT )
Beachte, dass die Dichten n und p unabhängig von E F sind.
Beispiele für Energielücken bei Raumtemperatur:
Material
E g (eV)
ni (cm-3)
Ge
Si
GaAs
Diamant (kein Halbleiter!)
0.67
1.12
1.43
5.4
2.4  1013
1.45  1010
1.79  10 6
Isolator
Für die Leitfähigkeit haben wir jetzt sowohl den Beitrag von Elektronen als auch von
Löchern zu berücksichtigen:
75900629
175
5/14/2016
2
ne 2 e pe  p
 E /( 2 k T )
 

e g B .
*
*
me
mp
Dabei haben wir beachtet, dass die Relaxationszeiten   v 1 w 1  T 3 / 2 ( w ist die
Stosswahrscheinlichkeit ) mit zunehmender Temperatur abnehmen:


mv 2
nicht-entartetes Gas:
 k BT , v  T 1 / 2
2
Phononenstreuung für T   : w  T
und den Faktor T 3 / 2 im Ausdruck für n kompensieren. Die Leitfähigkeit ist damit im
wesentlichen bestimmt durch die Ladungsträgerkonzentration n . Die folgende Figur
illustriert schön die exponentielle Zunahme von  mit der Temperatur (nach F. J. Morin
and J. P. Maita, Phys. Rev. 94, 1525 (1954)). Wie man sieht, tritt bei tiefen Temperaturen
ein anderer Mechanismus für die Stromleitung ein: Die Störstellenleitung, die wir im
folgenden Abschnitt behandeln.
-1
-1
Conductivity  ( cm )
Temperature (K)
StörstellenLeitung
Germanium
1/T (K-1)
5.3. Dotierte Halbleiter (doped semiconductors)
Die Störstellenleitung hängt sehr stark von der Reinheit des Halbleiters ab. Deshalb hat es
sehr lange gedauert, bis die Leitfähigkeit  von Ge und Si verstanden wurden. Man kann
75900629
176
5/14/2016
 nur gezielt verändern, wenn das Ausgangsmaterial rein genug ist. Dazu waren
Entwicklungen nötig auf dem Gebiet der Reinststoff-Forschung

Kristallzucht, Zonenschmelzen, Ausfällen, Isotopentrennung etc.
und der Nachweismethoden:




chemische Analyse:  1%
Spektralanalyse: bis 0.1 ppm
Massenspektroskopie
Neutronenaktivierung.
Betrachten wir, was passiert, wenn wir 4-wertiges Si (3s23p3) oder Ge mit 5-wertigem
Phosphor (3s23p2) dotieren. Es zeigt sich, dass das P ein Si ersetzt und nicht auf einen
Zwischengitterplatz geht. Es beteiligen sich also 4 Elektronen des Phosphor an der
kovalenten Bindung mit sogenannten sp3 Orbitalen.
Si
e-: antibindend
+
P
Die an der Bindung beteiligten Elektronen von P befinden sich im Valenzband. Das
antibindende, 5. Elektron hat eine höhere Energie. Es bleibt schwach gebunden zum
positiv geladenen Ion, wie ein Elektron in einem Wasserstoffatom (Bethe 1941).
Anhand des Modells eines Wasserstoffatoms kann die Ionisationsenergie des Elektrons
abgeschätzt werden. Aufgrund der dielektrischen Eigenschaften von Si ist die
Coulombwechselwirkung um  abgeschwächt. Weiter muss für die Masse des Elektrons
die effektive Masse der Leitungselektronen eingesetzt werden. Damit erhält man für die
Energieniveaus
E Dn  
me* e 4
m*e 1
1

13
.
6
eV
.
me ε 2
2(40 ) 2 n 2
Für Si ist me* / me  0.3 und   11.7 . Daraus folgt, dass die Ionisationsenergie des
Elektrons E D  30 meV beträgt. Dies entspricht einer Temperatur von k BT  400 K. Das