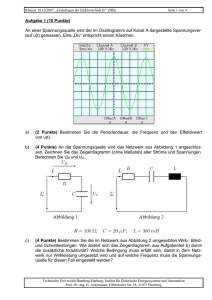
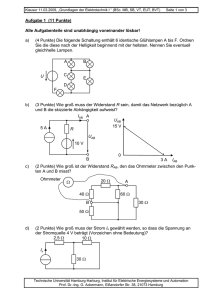
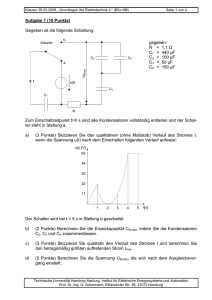
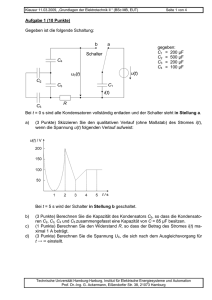
Eds 0 ⋅ = G G

Vorlesung "Grundlagen der Elektrotechnik II"
SS 2010
Wichtigste Punkte der Vorlesung am 07.04.10
1 ⋅ Q = 1⋅ Q
E
=
Punktladungen:
εo ⋅ εr 4π ⋅ r 2 ε A
εo
εr
(als Spezialfall "Kugel" aus allgemeinerem Gesetz)
= 8,85 ⋅10-12 As/Vm
allg. Dielektrizitätskonst.
= 1
Vakuum, Gase
rel. Dielektrizitätskonst.
= 2...6 Isolierstoffe;
= 80
Wasser
elektr. Feld:
bG
Feldlinienbild:
G
Uab = ∫ E ⋅ ds
a
wegunabhängig
G G
v∫ E ⋅ ds = 0
⇒ Potenzialfeld
E-Linien:
• kreuzen/verzweigen nicht
• Enden in Ladungen (+→ -)
• Dichte = Feldstärke
• ⊥ zu Leiteroberflächen
(Äquipotenzialflächen)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung "Grundlagen der Elektrotechnik II"
SS 2010
Wichtigste Punkte der Vorlesung am 14.04.10
Kapazität: C
Ladung, die bei
vorgegebener Spannung
aufgenommen werden kann:
a
C=Q/U
bG G
Uab = ∫ E ⋅ ds
b
a
Einheiten: 1
As
= 1F
V
1 mF = 10-3
1 µF = 10-6
1 nF = 10-9
1 pF = 10-12
F
F
F
F
parallele Platten (Plattenkondensator):
Elektrische Eigenschaften:
i = C⋅
u=
du
dt
1
⋅ ∫ i ⋅ dt
C
C = ε⋅A
d
⇒ Spannung kann
sich nicht
sprunghaft ändern
Parallelschaltung
Reihenschaltung
Cp = C1 + C2
CR =
C1 ⋅ C2
C1 + C2
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung "Grundlagen der Elektrotechnik II"
SS 2010
Wichtigste Punkte der Vorlesung am 21.04.10
gespeicherte Energie:
2
1
2 1 Q
W = ⋅C⋅ U = ⋅
2
2 C
Kraft zwischen parallelen Platten
F = 1 ⋅ε⋅ E2 ⋅ A
2
Berechnung der Kraft aus Energieänderung:
- z. B. virtuelle Verschiebung
- Systemgrenze beachten!
Anwendungsbeispiele:
- Füllstandssensor leitende Flüssigkeit
- Füllstandssensor nicht-leitende Flüssigkeit
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung "Grundlagen der Elektrotechnik II"
SS 2010
Wichtigste Punkte der Vorlesung am 28.04.10
magnetisches Feld
rechtswendig um Strom:
("Schraubenregel")
magnetische Feldstärke
H
A/m
magnetische Flussdichte
B = µ⋅H Vs/m2
µ = µ0⋅µr
µ0 = 0,4⋅π⋅10-6 Vs/Am Permeabilität des Vakuums
µr = 1
meiste Materialien
µr bis 106
ferromagnetische Materialien
(Fe, Ni, Co + Legierungen)
Kraft auf stromdurchflossenen Leiter
F ⊥ I,
F⊥B
F = I⋅B ⋅L
Durchflutungssatz:
G G
∫ H ⋅ ds = ∑ I = Θ
Mit Durchflutungssatz kann die
Feldstärke ausgerechnet werden,
wenn der Feldverlauf bekannt ist.
ds
I1
I2
I3
I4
Technische Universität Hamburg-Harburg, Institut für Elektrische Energieanlagen und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorferstr. 38, 21073 Hamburg
Vorlesung "Grundlagen der Elektrotechnik II"
SS 2010
Wichtigste Punkte der Vorlesung am 05.05.10
ferromagnetische Stoffe
ur >> 1
(ur ≈103...105)
Eisen, Stahl, Nickel, Kobalt, Legierungen daraus
Bei praktischen Anwendungen:
Durchflutung für Luftspalt >> Durchflutung für Eisenkreis
an Grenzflächen in der Luft:
Feldlinien parallel oder senkrecht zum Eisen
G G
magnetischer Fluß: Φ = ∫ B⋅ dA
oft:
Φ ↔ A !!
Φ=B⋅A
„Dichte der B-Linien“
„Anzahl der B-Linien“
Analogie
magnetisch
elektrisch
I
Φ
U
Θ
R = U/I
Rm = Θ/Φ
A
A
⋅ρ
R
=
Rm =
A
Aµ
Σ I = 0 (Knoten)
Σ Φ = 0 (Knoten)
Σ U = 0 (Masche)
Σ Θ = 0 (Masche)
Alle Regeln zur Berechnung von
Netzwerken gelten
Technische Universität Hamburg-Harburg, Institut für Elektrische Energieanlagen und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorferstr. 38, 21073 Hamburg
Vorlesung „Grundlagen der Elektrotechnik II“
SS 2010
Wichtigste Punkte der Vorlesung am 12.05.10
→
→
magnetischer Fluß: Φ = ∫ B• d A
A
Φ erfordert Angabe „welche Fläche“
Eisen:
Sättigung
µr >> 1
Bsätt = 1,5…2,5 T
Hysterese
(übertrieben
dargestellt)
B
Neukurve
H
Induktion
U=
• •
dΦ
, Φ durch Fläche der Schleife
dt
•
•
µ , H, A → Φ → u
Richtung: Wirkung versucht, Ursache zu bremsen
(Lenz`sche Regel)
Gegeninduktivität
Selbstinduktivität
Φ 2 (i1 )
Φ (i )
= M21 = 1 2
i1
i2
Φ (i )
L1 = 1 1
i1
M21 =
Zwei gekoppelte Spulen
d i1
dt
di
u1(i2) = M12 ⋅ 2 usw.
dt
u1(i1) = L ⋅
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation,
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung „Grundlagen der Elektrotechnik II“
SS 2010
Wichtigste Punkte der Vorlesung am 19.05.10
n
2
L= n
Rm
Energie, Energiedichte, Kraft
1
W = L · I2
2
dW
1
=
B2
dV 2 ⋅ µ
F
1
· B2
=
A 2µ o
A
B
idealer Transformator
bei zeitlich veränderlichen Größen („Wechselstrom“):
µFe → ∞, keine Streuung:
U1 n1 I 2
=
=
U 2 n 2 I1
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation,
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung „Grundlagen der Elektrotechnik II“
SS 2010
Wichtigste Punkte der Vorlesung am 09.06.2010
4wertiges Si, Ge im
Gitter
Dotierung
5wertig
Dotierung
3wertig
Keine freien Ladungsträger
→ keine Leitfähigkeit
Leitfähigkeit durch
Elektronen
„Leitfähigkeit durch Löcher“
(= fehlende Elektronen)
pn-Übergang:
Durchlassrichtung: Ladungsträger + ,-rekombinieren zu
Paaren
Sperrrichtung:
Paare müssten zerrissen werden
Diodenkennlinie:
Anwendungsbeispiele:
U
1.0A
I
Schaltzeichen
der Diode mit
Bezugspfeilen
I
0.5A
0.5
-1000V
-20mA
-40mA
1.0V
UD US
o Einweggleichrichter
o Zweiweggleichrichter
o mit Glättung
o Stabilisierung mit ZenerDiode
U
1) Durchbruch zerstörend
2) Zener-Durchbruch
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation,
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung „Grundlagen der Elektrotechnik II“
SS 2010
Wichtigste Punkte der Vorlesung am 16.06.2010
C
Transistor
- 3 Schichten npn oder pnp
- dünne Basis
- C-B Diode leitfähig durch
E-Ladungsträger, die in B
keinen Partner finden
n
Β
p
n
E
IC
IC
IB
U
Sättigung
CE
IB
U
BE
IE
≈UD
Schalter
Verstärker
UCE
IC = B ⋅ IB
B : Stromverstärkung
50 … 1.000
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation,
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung „Grundlagen der Elektrotechnik II“
SS 2010
Wichtigste Punkte der Vorlesung am 23.06.2010
Operationsverstärker
Ua = V0 (U+ - U_ )
- (UB - U∆) < Ua < (UB - U∆)
U∆ ≈ 1...2V
V0 → ∞
Gegenkopplung
Ausgangssignal wird mit negativem Vorzeichen auf
Eingang zurückgeleitet
→ Verstärkung nur von Rückkopplungsbauelementen
bestimmt
„Rezept“ zur Berechnung
Gilt wenn: - Gegenkopplung (Weg Ua → U_)
- Ua nicht in Begrenzung
1: U+ = U_ (wegen V0 → ∞)
2: i+ = i_ = 0
Dann Maschen/Knotengleichungen
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation,
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung „Grundlagen der Elektrotechnik II“
SS 2010
Wichtigste Punkte der Vorlesung am 30.06.10
„Rezept“ zur Berechnung bei Gegenkopplung
Gilt wenn: - Gegenkopplung (VZ-Wechsel im
Kreis)
- UA nicht in Begrenzung
1: U+ = U- (wegen V0 → ∞)
2: i+ = i- = 0
Dann Maschen/Knotengleichungen
(Bei nichtlinearen Elementen ggf. Fallunterscheidung)
Mitkopplung
Einsatz als Vergleicher (Komparator) mit
Hysterese
Fallunterscheidung:
UA = Umax
UA = - Umax
Mit „Rezept“ Umschaltpunkte berechnen.
Beispiele Operationsverstärker
- Anwendung: Mit- u. Gegenkopplung (Motor n =
const.)
Feldeffekttransistor (FET, MOSFET)
Verdrängung der Ladungsträger, Einschnürung der leitenden
Bahn.
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation,
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung „Grundlagen der Elektrotechnik II“
SS 2010
Wichtigste Punkte der Vorlesung am 07.07.2010
Thyristor:
Schalter:
Einschalten: iG > 0, uAK > 0
Ausschalten: iA < 0
Gesteuerter Gleichrichter
io
4
a
1
L
uo
u X = uR
1-3
u
i
L=0
2-4
1-3
t
3
2
uX
uR
R
uo
L ∞
uX
uR
u
Die mittlere Spannung kann
durch den Zündwinkel eingestellt werden.
t
uo
uo
Zündwinkel α
Dimmer: Mit Triac, Stromfluss in beide Richtungen
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation,
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg
Vorlesung "Grundlagen der Elektrotechnik II"
SS 2010
Wichtigste Punkte der Vorlesung am 14.07.2010
Beispiele:
− Gleichrichter für Drehstrom
− Hochsetzstelle
− Feldmessung Hochspannungsfreileitung (s. separates
Dokument)
Technische Universität Hamburg-Harburg, Institut für Elektrische Energiesysteme und Automation
Prof. Dr.-Ing. G. Ackermann, Eißendorfer Str. 38, 21073 Hamburg