Stetige Zufallsvariablen und Wahrscheinlichkeitsverteilungen

Für eine stetige Zufallsvariable X in einem Intervall [ a ; b ] kann X jeden beliebigen Wert
annehmen. Die Wahrscheinlichkeiten werden in diesem Fall nicht mehr wie bei einer
diskreten Zufallsvariable auf nur bestimmte Punkte xk konzentriert, sondern sind
kontinuierlich im Intervall a X b verteilt. Für einen xk-Wert einer diskreten
Zufallsvariable liefert die Wahrscheinlichkeitsfunktion f ( xk ) die Wahrscheinlichkeit
P ( X = xk ) oder in einem bestimmten Intervall [ a ; b ] ist die Wahrscheinlichkeit
P ( a X b ) die Summe der jeweiligen Wahrscheinlichkeiten für die verschiedenen xk Werte in diesem Intervall. Dagegen für eine stetige Zufallsvariable sind die x-Werte in
einem Intervall [ a ; b ] so viele, dass sie nicht mehr abzählbar sind und folglich deren
Wahrscheinlichkeiten auch nicht aufsummiert werden können. Somit wird die
Wahrscheinlichkeit einer stetigen Zufallsvariable in einem Intervall mit Hilfe der
Wahrscheinlichkeitsdichte oder Dichtefunktion f ( x ) angegeben. Die Wahrscheinlichkeit
in einem Intervall a X b wird durch die Fläche unterhalb der Dichtefunktion in diesem
Intervall repräsentiert.
Aus der Serienproduktion zur Herstellung von Autobatterien wurde eine Stichprobe vom
Umfang N = 40 entnommen. Die Messungen der Lebensdauer X (in Jahren) der Batterien
ergab die folgende Tabelle für Häufigkeitsverteilung:
j
K
1
2
3
4
5
6
7
d
j
[ 1,5
[ 2,0
[ 2,5
[ 3,0
[ 3,5
[ 4,0
[ 4,5
;
;
;
;
;
;
;
2,0 )
2,5 )
3,0 )
3,5 )
4,0 )
4,5 )
5,0 )
j
0,5
0,5
0,5
0,5
0,5
0,5
0,5
mj
1,75
2,25
2,75
3,25
3,75
4,25
4,75
hj
2
1
4
15
10
5
3
fj
f
0,05
0,025
0,1
0,375
0,25
0,125
0,075
*
j
f
:=
d
Fj
j
j
0,1
0,05
0,2
0,75
0,5
0,25
0,15
0,05
0.075
0,175
0,55
0,8
0,925
1
Zeichnen Sie
ein Histogramm der relativen Häufigkeiten.
ein Dichtehistogramm der Klassendichten der relativen Häufigkeiten und ein
Häufigkeitspolygon
ein geglättetes relatives Häufigkeitspolygon
Wie groß ist die Wahrscheinlichkeit dafür, dass eine zufällig aus der Produktion
entnommene Batterie eine Lebensdauer zwischen 3,5 bis 4,5 Jahre hat?
1
j
0,375
0,250
0,125
Klassendichte der relative Häufigkeiten
0
1,75 2,25 2,75 3,25 3,75 4,25 4,75
1,5
5
Lebensdauer [Jahre]
Klassendichte der relative Häufigkeiten
Relative Häufigkeiten
f
0,75
0,50
0,25
0
1,25 1,75 2,25 2,75 3,25 3,75 4,25 4,75 5,25
1,5
5
Lebensdauer [Jahre]
Die Wahrscheinlichkeit, dass eine zufällig
entnommene Batterie eine Lebensdauer
zwischen 3,5 bis 4,5 Jahre hat, ist der
Flächeninhalt des 5. und 6. Rechteckes, d.h.
0,5⋅0,5 + 0,5⋅0,25 = 0,375 oder die Fläche
unterhalb des Häufigkeitspolygons oder
näherungsweise die gefärbte Fläche unterhalb
der Glockenkurve des geglätteten
Häufigkeitspolygons (Dichtefunktion).
0,75
0,50
0,25
1,75
0
f *j
2,25 2,75 3,25 3,75 4,25 4,75
Lebensdauer [Jahre]
Zeichnen Sie für Daten des vorigen Beispiels
ein kumulatives relatives Häufigkeitspolygon (die empirische Verteilungsfunktion)
ein geglättetes kumulatives relatives Häufigkeitspolygon.
Wie groß ist die Wahrscheinlichkeit dafür, dass eine zufällig aus der Produktion
entnommene Batterie eine Lebensdauer weniger als 3,5 Jahre hat?
Häufigkeiten
Fj
!
#
"
Kumulierte Relative Häufigkeiten
1,0
0,75
0,50
0,25
0
1,5
2,0
2,5
3,0
3,5
4,0
4,5
5,0
Lebensdauer [Jahre]
"
Lebensdauer [Jahre]
3,5
P ( X ≤ 3 ,5
) = F (3,5 ) =
f ( x ) dx ≈ 0 , 55
− ∞
2
$%
(
&
$% %
"
'
'
(
Stetige Zufallsvariable
Eine Zufallsvariable heißt stetig, wenn sie jeden beliebigen reellen Wert in einem endlichen
oder unendlichen Intervall annehmen kann.
$% %) &
!
'
(
Dichtefunktion (Wahrscheinlichkeitsdichte)
Die Wahrscheinlichkeitsverteilung einer stetigen Zufallsvariable X lässt sich durch die
Dichtefunktion oder Wahrscheinlichkeitsdichte
f(x)
beschreiben oder durch die dazugehörige Verteilungsfunktion:
x
F (x ) = P ( X ≤ x
)
f (u ) du
=
− ∞
darstellen.
Die Dichtefunktion erfüllt folgende Eigenschaften:
f(x)
0
f ist stetig bis auf endliche Punkte
∞
f ( x ) dx = 1
− ∞
)2ba
Die Flugdauer X (in Minuten) einer Airline für Flüge von Berlin nach Rom sei eine stetige
Zufallsvariable. Die Flugdauer für diese Flugstrecke kann zwischen 120 und 140 Minuten
dauern. Die Dichtefunktion, die diesen Flug beschreibt sei wie folgt:
f (x
)=
0
1
20
0
für
für
für
x < 120
120 ≤ x ≤ 140
x > 140
Zeigen Sie, dass f eine Dichtefunktion ist..
Bestimmen Sie die Verteilungsfunktion und stellen Sie die Wahrscheinlichkeitsverteilung
von X graphisch dar.
Wie groß ist der Anteil an Flügen für diese Strecke, die weniger als 130 Minuten dauern?
3
*+
Die Dichtefunktion ist in dem
Definitionsbereich [120 ; 140] positiv.
f(x)
Die Dichte Funktion ist in dem
Definitionsbereich [120 ; 140] stetig.
1/20
Es muss noch überprüft werden, ob
∞
f ( x ) dx = 1 gilt:
0
120
Flugdauer [min]
∞
140
120
f ( x )d x =
− ∞
140
0 dx +
120
− ∞
0
=
x
− ∞
20
0 dx
dx +
20
1
+
∞
1
140
140
x
+
0
= 1
120
Die Verteilungsfunktion ist:
x
120
F(x) =
f (u )d u =
− ∞
x
120
− ∞
=
0
0
F (x
1
) =
F(x)
1
0 du +
x − 6
20
1
1
+
20
20
du
x − 6
x < 120
für
120 ≤ x ≤ 140
für
x > 140
für
"
1
0
120
Flugdauer [min]
140
x
4
Die Wahrscheinlichkeit für alle Flugdauern unterhalb von X = 130 Minuten ist:
130
F ( 130 ) = P ( X ≤ 130
)=
120
f ( x )d x =
− ∞
130
0 ⋅d x +
120
− ∞
1
= 0 +
20
130
x
1
=
20
120
⋅ 130
1
20
⋅d x
−
1
20
⋅ 120
= 0,5
f(x)
F(x)
1
1/20
0,5
0
"
120
0,5
130
Flugdauer [min]
140
0
x
120
130
Flugdauer [min]
140
x
,
Wie groß ist der Anteil an Flügen für die Flugstrecke des vorigen Beispiels, die mehr als 125
Minuten dauern?
*+
∞
f ( x ) dx = 1
Für die Gesamtwahrscheinlichkeit der Dichtefunktion gilt
− ∞
Folglich ist die Wahrscheinlichkeit für alle Flugdauern oberhalb von X = 130 Minuten ist:
P ( X > 130 ) = 1 −
[
P ( X ≤ 130 )
]
= 1 − F ( 130 ) = 1 − 0 , 5 = 0 , 5
f(x)
1/20
0
120
130
Flugdauer [min]
140
x
5
$%) "
&
'
Ähnlich den Maßzahlen in der beschreibenden Statistik ordnet man der
Wahrscheinlichkeitsverteilung einer Zufallsvariable X Kennwerte oder Maßzahlen zu. Zu
ihnen zählen der Mittelwert (Erwartungswert) und die Varianz bzw. die Standardabweichung.
$%)%
&
! .
.
/0
.
!
'
Erwartungswert µ = E[ X ] einer Stetigen Zufallsvariable
Der Erwartungswert E[ X ] einer stetigen Zufallsvariable X ist:
∞
µ = E[X ] =
x ⋅ f ( x ) dx
,
− ∞
Dabei ist f ( x ) die Dichtefunktion der stetigen Zufallsvariable.
12ba
Die Flugdauer X (in Minuten) einer Airline für Flüge von Berlin nach Rom sei eine stetige
Zufallsvariable mit der Dichtefunktion:
1
f (x) =
für
20
120 ≤ x ≤ 140
0
sonst
Berechnen Sie die mittlere Flugdauer für diese Flugstrecke.
*+
∞
120
x ⋅ f ( x )d x =
µ =
− ∞
140
x ⋅0 d x +
120
− ∞
=
x⋅
0
+
1
20
⋅
x2
2
1
20
∞
x⋅0 d x
dx +
140
140
+
0
= 130
120
Also beträgt die mittlere Flugdauer für diese Flugstrecke 130 Minuten.
6
$%)%)
&
"
Varianz
23
'
.
!
² = Var[ X ] und Standardabweichung
Die Varianz
'
einer stetigen Zufallsvariable
² einer stetigen Zufallsvariable X ist:
∞
σ
2
= Var [ X
]
f (x )⋅ ( x − µ
=
) 2 dx
− ∞
Dabei sind f ( x ) die Dichtefunktion und µ der Erwartungswert der stetigen
Zufallsvariable.
Die Standardabweichung ist: σ =
σ
2
Die Varianz für stetige Zufallsvariablen kann auch mit der bequemeren Formel
berechnet werden.
∞
σ
2
f (x)⋅ x
=
2
dx
− µ
2
− ∞
,
)
Die Flugdauer X (in Minuten) einer Airline für Flüge von Berlin nach Rom sei eine stetige
Zufallsvariable mit der Dichtefunktion:
1
f (x
)=
20
0
für
120 ≤ x ≤ 140
sonst
Die mittlere Flugdauer für diese Flugstrecke beträgt 130 Minuten (s. voriges Beispiel: Bsp. 3)
Berechnen Sie die Standardabweichung der Flugdauer für diese Flugstrecke.
*+
-
7
$%)%1
4
!
'
&
Das q-Quantil mit 0 < q < 1 ist der x-Wert, der die Gesamtfläche unterhalb der
Dichtefunktion f ( x ) in zwei Teilflächen aufteilt, so dass links von ihm der Inhalt der einen
Teilfläche q und rechts von ihm der Inhalt der anderen Teilfläche ( 1 – q ) beträgt. Der
Flächeninhalt unter dem Graphen der Dichtefunktion f ( x ) bis zu einem beliebigen x-Wert
wird durch den Funktionswert der Verteilungsfunktion F ( x ) bei diesem x-Wert angegeben.
Wenn die Verteilungsfunktion F streng monoton wachsend ist, dann lassen sich die
Quantilen mit Hilfe dieser Verteilungsfunktion bestimmen.
Quantile einer stetigen Wahrscheinlichkeitsverteilung
Das q-Quantil xq mit 0 < q < 1 einer stetigen Wahrscheinlichkeitsverteilung ist die
Zahl auf der x-Achse, für die gilt:
F ( xq ) = q ,
falls die Verteilungsfunktion F streng monoton wachsend ist
,
1
Die Flugdauer X (in Minuten) einer Airline für Flüge von Berlin nach Rom sei eine stetige
Zufallsvariable mit der Verteilungsfunktion:
0
F (x
) =
1
x < 120
für
x − 6
20
1
für
120 ≤ x ≤ 140
für
x > 140
Bestimmen Sie das 0,25-Quantil x 0,25 der Flugdauer für diese Flugstrecke.
f(x)
1/20
xq
0
F(x)
Fläche F (xq)
:
q = 0,25
*+
120
x0,25
Flugdauer [min]
"
1
F (xq)
xq
q = 0,25
140 x
0
120 x0,25
Flugdauer [min]
140
x
8
'
2
'
&
In den folgenden Abschnitten werden einige wichtige stetige
Wahrscheinlichkeitsverteilungen vorgestellt, die in der Technik, Naturwissenschaften und
in der Statistik eine wichtige Rolle spielen.
$%1
5
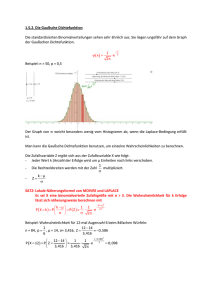
Die Gaußsche Normalverteilung spielt eine wichtige Rolle in der
Wahrscheinlichkeitsrechnung und Statistik. Die Verteilung von vielen stetigen
Zufallsvariablen in der Technik und den Naturwissenschaften wie z.B. physikalisch
technische Messgrößen können durch die Dichtefunktion der Normalverteilung beschrieben
werden. Bei vielen Messwerten, die von vielen Einzeleinflüssen beeinflusst werden, häufen
sich die Werte in der Nähe des Mittelwerts (Sollwert). Die Dichtekurve die Form einer
Glockenkurve besitzt.
6
Aus der Serienproduktion zur Herstellung von Autobatterien wurde eine Stichprobe vom
Umfang N = 40 entnommen. Die Messungen der Lebensdauer X (in Jahren) der Batterien
ergab die folgende Tabelle für die Häufigkeitsverteilung:
j
Kj
1
2
3
4
5
6
7
[ 1,5
[ 2,0
[ 2,5
[ 3,0
[ 3,5
[ 4,0
[ 4,5
dj
;
;
;
;
;
;
;
2,0 )
2,5 )
3,0 )
3,5 )
4,0 )
4,5 )
5,0 )
mj
0,5
0,5
0,5
0,5
0,5
0,5
0,5
hj
1,75
2,25
2,75
3,25
3,75
4,25
4,75
fj
2
1
4
15
10
5
3
f
Fj
j
0,05
0,025
0,1
0,375
0,25
0,125
0,075
0,1
0,05
0,2
0,75
0,5
0,25
0,15
0,05
0.075
0,175
0,55
0,8
0,925
1
In der Abbildung sind das Dichtehistogramm sowie die Kurve der Dichtefunktion, die an den
Messdaten angepasst wurde, dargestellt.
7
0,75
0,50
0,25
0
1,75 2,25 2,75 3,25 3,75 4,25 4,75 x
3,5
4,5 [Jahre]
Die approximierte Dichtefunktion lautet:
f (x) =
1
2 π ⋅ 0 , 53
2
exp
−
1
x − 3 , 37
2
0 , 53
2
7
Wie groß ist die Wahrscheinlichkeit, dass eine zufällig aus der Produktion entnommene
Batterie eine Lebensdauer zwischen 3,5 bis 4,5 Jahre hat?
9
*+
Der Flächeninhalt des 5. und 6. Rechteckes:
0,5 ⋅ 0,5 + 0,5 ⋅ 0,25 = 0,375
Der Inhalt der Fläche unterhalb des Graphen der an dem Histogramm approximierten
Dichtefunktion zwischen den Grenzen 2 und 4:
P ( 3 ,5 ≤ X ≤ 4 ,5 ) =
4,5
1
2 π ⋅ 0 , 53
−
e
⋅
1
x − 3 , 37
2
0 , 53
2
dx = 0 , 386
3,5
Der Wert dieses Integral muss numerisch berechnet werden.
$%1%
8
5
Gaußsche Normal-Verteilung
Die Verteilung einer stetigen Zufallsvariable X mit der Dichtefunktion:
1
f (x) =
2π σ
exp
2
−
1
x − µ
2
σ
2
heißt Gaußsche Normalverteilung.
Dabei sind die Parameter
der Erwartungswert und
X kann die Werte : – ∞ < x < ∞ annehmen.
² die Varianz dieser Verteilung.
Die Verteilungsfunktion der Gaußschen Normalverteilung ist:
x
1
− ∞
2π σ
F( x ) = P( X ≤ x ) =
2
exp
−
1
u − µ
2
σ
2
du
5
"
µ=0
σ =1
f(x)
µ=0
σ =2
µ=2
σ =1
µ=–2
σ =2
–4
–2
0
2
4
x
10
Eigenschaften der Normalverteilung
Die Kurve der Dichtefunktion der Normalverteilung ist symmetrisch bzgl. der Gerade
x=
Für eine normalverteilte Zufallsvariable liegen
ca. 68,2%
ca. 95%
ca. 99.7%
der beobachteten Werte zwischen
der beobachteten Werte zwischen
der beobachteten Werte zwischen
σ
σ
$%1%)
σ
σ
µ
–
– 2
– 3
σ
und
und
und
+
+2
+3
σ
&
7
5
7
8
5
Möchte man für eine stetige Zufallsvariable, deren Verteilung durch die Normalverteilung
gegeben ist, die Wahrscheinlichkeit für alle Werte „kleiner als einen bestimmten Wert x0
bestimmen, so berechnet man definitionsgemäß folgendes Integral
xo
P ( X ≤ xo
)
= F (xo
)=
f ( x ) dx =
− ∞
xo
1
2π σ
2
exp
− ∞
−
1
x − µ
2
σ
2
dx
Leider kann F ( x ) , d.h. die Stammfunktion der Dichtefunktion f ( x ) der
Normalverteilung nicht analytisch mit Hilfe von Integraltechniken bestimmt werden. Der
Wert des Integrals muss numerisch berechnet werden.
11
6
Die Lebensdauer X (in Jahren) der Batterien einer Serienproduktion sei eine
normalverteilte Zufallsgröße mit der Dichtefunktion: (s. Bsp. 4)
f(x )
f (x
)=
1
−
2 π ⋅ 0 , 53
mit µ = 3,37 und
e
1
x − 3 , 37
2
0 , 53
2
P(X
3,5 )
σ = 0,53
µ = 3,37
= 0,53
2
3 µ
4
5
x
3,5
Wie groß ist die Wahrscheinlichkeit, dass eine zufällig aus der Produktion entnommene
Batterie eine Lebensdauer weniger als 3,5 Jahre hat?
*+
-
P ( X ≤ 3 ,5 ) = F ( 3 ,5 ) =
$%1%1 '
&
5
1
2 π ⋅ 0 , 53
3,5
−
e
⋅
1
x − 3 , 37
2
0 , 53
2
dx = 0 , 596
− ∞
"
"
5
Da die Stammfunktion F (x ) der Dichtefunktion f (x ) der Normalverteilung nicht bestimmt
werden kann, muss der Wert für F (x0 ) für einen beliebigen x0 numerisch berechnet werden.
Man kann also numerische berechnete Werte-Tabellen erstellen, die für verschiedene xWerte sowie - und -Werten die dazugehörigen F (x ) enthalten. Leider werden solche
Tabellen sehr groß und unübersichtlich.
Geht man aber von einer beliebigen normalverteilten Zufallsvariable X durch die lineare
Transformation (Substitution) zu der standardisierten Variable:
Z =
X − µ
σ
über, so genügt die Zufallsvariable Z auch einer Normalverteilung mit = 0 und
=1
Somit lassen sich alle Normalverteilungen durch die Standardisierung auf eine einzige
Verteilung zurückführen.
12
Standard-Normalverteilung
Die Verteilung einer stetigen Zufallsvariable Z mit der Dichtefunktion:
ϕ(z
)
=
1
exp
2π
−
1 2
z
2
heißt Standardnormalverteilung.
Dabei sind die Parameter
= 0 und
² = 1.
Ihre Verteilungsfunktion lautet:
z
Φ( z
)
= P(Z ≤ z
)
=
− ∞
1
2π
exp
−
1
v
2
2
dv
Im Anhang befindet sich eine Tabelle mit den Werten der Verteilungsfunktion Φ ( z ) der
Standard-Normalverteilung für beliebige z.
Mit Hilfe der Standard-Normalverteilung kann die Wahrscheinlichkeit F (x0 ) = P ( X
bestimmt werden.
x0 )
Φ ( z)
P(Z
z0 ) = Φ ( z0 )
z
(z)
P(Z
z0 )
z
z0
z.B. für z 0 = 0,76 beträgt die Wahrscheinlichkeit P ( Z
0,76 ) = Φ ( 0,76 ) = 0,7764
13
Beziehung zur Bestimmung der Wahrscheinlichkeit P ( X x0 ) einer beliebigen
normalverteilten Zufallsvariable X mit Hilfe der Standard-Normalverteilung
P(X
x0 )
P(Z
=
F ( x0 )
z0 )
Φ ( z0 )
=
(z)
F ( x0 )
f(x)
Φ ( z0 )
=
0
µ
xo
1
2π σ
z =
x0
2
x − µ
σ
exp
−
−∞
x
1
x − µ
2
σ
dz =
1
σ
z
z0
0
2
dx
zo
1
dx
exp
2π
−∞
−
1
2
z
2
dz
6
Bestimmen Sie mit Hilfe der Tabelle für die Werte der Verteilungsfunktion der StandardNormalverteilung die Wahrscheinlichkeit aus dem vorigen Beispiel dafür, dass eine zufällig
aus der Produktion entnommene Batterie eine Lebensdauer weniger als 3,5 Jahre hat?
Die Lebensdauerverteilung entspricht einer Normalverteilung mit:
µ = 3,37 und
= 0,53 .
*+
Es soll die Wahrscheinlichkeit für alle x-Werte kleiner als die obere Grenze x0 = 3,5
berechnet werden. Die Substitution liefert folgende obere Grenze für die Zufallsvariable Z:
Z =
X − µ
σ
zo
=
xo − µ
σ
=
3 , 5 − 3 , 37
0 , 53
= 0 , 245
Somit erhält man für die gesuchte Wahrscheinlichkeit:
14
(z)
f(x )
P(X
z²
exp
2
3,5 )
Z =
2
1
(z)=
3 3,5 4
P(X
3,5 )
5
Φ ( 0,245 )
X –
0 z0 = 0,245
x
=
=
2
P(Z
z
0,245 )
Φ ( 0,245 )
≈ 0,5967
Da in der Tabelle der Wert z 0 = 0,245 nicht eingetragen ist, wird die
Wahrscheinlichkeit Φ ( 0,245 ) näherungsweise als das arithmetische Mittel der
Wahrscheinlichkeiten Φ ( z ) für die beiden benachbarten z-Werten angegeben.
Φ ( 0,245 ) = ½ [ Φ ( 0,24 ) + Φ ( 0,25 ) ] = ½ [ 0,5948 + 0,5987 ] = 0,5967
Liegt ein z 0-Wert mit mehr als 2 Nachkommastellen vor, so kann Φ ( z 0) aus der Tabelle der
Standard-Normal-Verteilung genauer durch lineare Interpolation bestimmt werden.
,
6
Geben Sie mit Hilfe der Tabelle für die Werte der Verteilungsfunktion der StandardNormalverteilung die Wahrscheinlichkeit aus dem vorigen Beispiel dafür an, dass eine
zufällig aus der Produktion entnommene Batterie eine Lebensdauer weniger als 4,5 Jahre
hat?
*+
-
P( X
4,5 ) = P( z
2,132 ) = Φ (2,132) = 0,9834
6
Bestimmen Sie mit Hilfe der Werte für die Verteilungsfunktion der Standard-Normalverteilung
die Wahrscheinlichkeit aus dem vorigen Beispiel dafür, dass eine zufällig aus der Produktion
entnommene Batterie eine Lebensdauer zwischen 3,5 und 4,5 Jahre hat?
15
*+
Gesucht ist also: P ( 3,5
f(x)
P ( 3,5
X
4,5 ) = ?
X
4,5 )
0.7
0.6
0.5
0.4
0.3
0.2
0.1
8
5
P(X
3,5 )
"
=
2
3 3,5 4 4,5 5
P(X
f(x)
6
x
4,5 )
f(x)
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.7
0.6
0.5
0.4
0.3
0.2
0.1
–
2
3
4 4,5 5
6x
2
3
3,5 4
5
'
P ( 0,245
ϕ(z)
5
"
2,13 )
Z
0.7
0.6
0.5
0.4
0.3
0.2
0.1
x
=
2
3
4 2,135
0
0,245
ϕ(z)
P(Z
6 z
P(Z
ϕ(z)
2,13 )
0,245 )
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.7
0.6
0.5
0.4
0.3
0.2
0.1
–
2
P ( 3,5
3
0
X
4
2,13 5
4,5 ) =
=
=
2
6z
P ( 0,245
P(Z
Z
2,13 ) –
0,9834
3 0 0,245
4
–
5
z
2,13 )
P(Z
0,5967
0,245 )
=
0,3867
16
Formel zur Bestimmung der Wahrscheinlichkeiten einer normalverteilten
Zufallsvariable X zwischen zwei x-Werten a und b :
folgt:
Aus der Beziehung
P(a
P(Z
b)
X
b) –
F ( b) –
P(Z
F(a)
P(z1
=
a)
=
P(Z
z2) –
Φ ( z 2)
=
f ( x)
z2)
Z
P(Z
–
z1)
Φ(z1)
( z)
Φ ( z2 ) – Φ ( z1 )
F ( b) – F ( a )
σ
a
µ
b
z1 0
x
z2
z
Formel zur Bestimmung der Wahrscheinlichkeiten mit der Standardnormalverteilung für negative Wert von z :
Da die Dichtefunktion der Standardnormalverteilung symmetrisch zu 0 ist, gilt:
Φ (– z ) = 1 – Φ (z )
9
Der Durchmesse X von seriengefertigten Kugeln sei eine normalverteilte Zufallsgröße.
Langzeitige Messungen des Durchmessers von mehreren hergestellten Kugeln ergab eine
Normalverteilung mit = 50 [mm] und
= 10 [mm]. Geben Sie an, welcher Anteil der
hergestellten Kugeln einen Durchmesser zwischen 45 [mm] und 62 [mm] hat.
*+
Normalverteilung mit
= 50 [mm] und
= 10 [mm].
Der Anteil der Kugel mit einem Durchmesser zwischen a = 45 [mm] und b = 62 [mm]
muss berechnet werden. Dafür soll die Wahrscheinlichkeit für alle x-Werte zwischen den
Grenzen x1 = 45 und x2 = 62 berechnet werden.
17
1. Lösungsweg mit Hilfe des Integrals:
P ( 45 ≤ X ≤ 62
)
62
1
=
2 π 10 2
e
−
1
2
x − 50
10
2
dx = F ( 62
)
− F ( 45
)
45
Dieses Integral können wir numerisch mit Hilfe des Taschenrechners ausrechnen, denn
die beiden Grenzen sind Zahlen. Oder wir verwenden die Standard-Normal-Verteilung.
2. Lösungsweg mit Hilfe der Tabelle der Standard-Normal-Verteilung:
Die Substitution liefert folgende Grenzen für die Zufallsvariable Z:
Z =
X − µ
σ
z
1
z
2
=
=
45 − 50
10
62 − 50
10
= − 0,5
1, 2
=
Somit erhält man für die gesuchte Wahrscheinlichkeit:
(z)
1
(z)=
exp
2
z²
2
F (62) – F(45)
f(x)
Z =
σ
4
0
a = 45
µ
P ( 45
6
σ
0
b = 62
X
Φ (1,2) – Φ (– 0,5)
X – µ
62 )
x
z1 = – 0,5
0
z2 = 1,2
=
P ( – 0,5
=
Φ ( 1,2 ) – Φ ( – 0,5 )
=
0,8849
Z
–
z
1,2 )
0,3085
= 0,5764
18
$%1%6 4
5
Das q-Quantil z q mit 0 < q < 1 teilt die Fläche unter dem Graphen der Standard-NormalVerteilung ϕ ( z ) in 2 Teilflächen, so dass links von ihm der Inhalt der einen Teilfläche q
und rechts von ihm der Inhalt der anderen Teilfläche 1 – q beträgt.
(z)
P(Z
zq ) = q
Φ ( zq ) = q
q
zq
0
z
Quantilen / Perzentilen der Normal-Verteilung
Das q-Quantil z q mit 0 < q < 1 der Sandard-Normal-Verteilung ist die Zahl auf
der z-Achse , für die gilt:
Φ(zq) = q
Das q-Quantil x q mit 0 < q < 1 der Gaußschen Normal-Verteilung ist die Zahl auf
der x-Achse , für die gilt:
F(xq) = q
Dieses lässt sich dann mit Hilfe von z q wie folgt berechnen:
zq
=
xq − µ
σ
⇔
xq = σ ·zq + µ
,
9
Bestimmen Sie das 0,025-Quantil (2,5%-Quantil) x 0,025 für die Verteilung der
Lebensdauer der Batterien aus Bsp. 4.
*+
-
19
$%6
!:
Die Exponentialverteilung spielt eine wichtige Rolle in der Warteschlangentheorie (queuing
theory) und Zuverlässigkeit von Systemen (reliability problems). Die Verteilung der
Lebensdauer z.B. von Bauteilen kann durch die Dichtefunktion der Exponentialverteilung
beschrieben werden.
$
Die Lebensdauern in (Jahren) von 40 baugleichen elektronischen Dioden einer
Serienproduktion wurden gemessen.
0,2
1,5
2,7
4,8
0,3
1,6
2,78
5,0
0,4
1,72
3,1
5,8
0,55
1,8
3,2
5,99
0,6
1,9
3,8
6,0
0,8
1,92
3,96
6,7
0,84
2,0
4,1
7,0
1,0
2,1
4,32
7,4
1,2
2,35
4,5
8,6
1,45
2,5
4,65
9,4
Aus den Ergebnissen der Messungen wurde die folgende klassierte Häufigkeitstabelle
erstellt.
Klasse
Kj
[0 ; 2)
[2 ; 4)
[4 ; 6)
[6 ; 8)
[8 ; 10)
j
1
2
3
4
5
KlassenBreite: d j
2–0=2
2
2
2
2
KlassenMitte: m j
½ (0+2) = 1
3
5
7
9
Abs.
Häuf. h j
16
10
8
4
2
Rel. Häuf.
fj
16 40 = 0,4
0,25
0,2
0,1
0,05
Klassendichte: Kumulierte
Häufig. F j
f j
0,4
0,4 2 = 0,2
0,125
0,65
0,1
0,85
0,05
0,95
0,025
1
In der Abbildung sind das Dichte-Histogramm und die Kurve der Dichtefunktion, die an den
Messdaten angepasst wurde, dargestellt.
j
Häufig.
f
f(x)
0.3
Die approximierte Dichtefunktion lautet:
0.25
0.2
f (x
0.15
)=
0
0,3 e
für
− 0,3 x
für
x ≤ 0
x > 0
0.1
0.05
x
0
2
4
6
8
10
12
7
Wie groß ist die Wahrscheinlichkeit, dass eine Diode eine Lebensdauer zwischen 2 bis 4
Jahren besitzt?
*+
Mit Hilfe des Dichte-Histogramms:
Der Flächeninhalt des 2. Rechteckes:
2 ⋅ 0,125 = 0,25
20
Mit Hilfe der Dichtefunktion:
Der Flächeninhalt unterhalb des Graphen der Dichtefunktion zwischen den Grenzen 2
und 4:
P (2 ≤ X ≤ 4) =
4
2
0 ,3 e
− 0,3 x
dx = 0 , 247
Exponential-Verteilung
Die Verteilung einer stetigen Zufallsvariable X mit der Dichtefunktion:
0
f (x
x ≤ 0
für
)=
,
− αx
α e
α >0
mit
x > 0
für
heißt Exponetialverteilung.
Die Verteilungsfunktion der Exponentialverteilung lautet:
0
x
F(x
) = P(X ≤ x ) =
f ( u ) du
für
=
1− e
− ∞
− αx
F(x)
f(x)
!:
x ≤ 0
"
für
x > 0
"
!:
"
1
0.14
F ( x0 )
0.12
F ( x0 ) = P ( X
0.1
x0 )
0.08
0.06
0.04
x
0.02
0
5
x100
15
x
0
20
x0
Satz: Erwartungswert und Varianz der Exponential-Verteilung
Der Erwartungswert der Exponential-Verteilung ist:
∞
x ⋅ f ( x ) dx =
µ =
− ∞
1
α
Die Varianz der Exponential-Verteilung ist:
∞
σ
2
2
f ( x ) ⋅ ( x − µ ) dx =
=
− ∞
1
2
α
21
,
$
Die Wahrscheinlichkeitsverteilung der Lebensdauer X aus dem vorigen Beispiel (Bsp. 6)
wurde durch die folgende Dichtefunktion gegeben:
– 0,3 x
f ( x ) = 0,3 e
, für x > 0
Geben Sie mit Hilfe der Verteilungsfunktion die Wahrscheinlichkeit dafür an, dass die
Lebensdauer einer Diode zwischen 2 bis 4 Jahren beträgt.
Geben Sie die durchschnittliche Lebensdauer an.
Geben Sie die Varianz (bzw. die Standardabweichung) der Verteilung der Lebensdauer
an.
*+
-
Satz: Quantilen der Exponential-Verteilung
Das q-Quantil xq mit 0 < q < 1 der Exponentialverteilung ist die Zahl auf der x-Achse,
für die gilt:
F (xq ) = q
1− e
Folglich lässt sich das q-Quantil xq
xq
=
− α⋅ xq
!:
q
der Exponentialverteilung wie folgt bestimmen:
−
ln ( 1 − q )
α
F(x)
f(x)
=
1
"
"
!:
"
F (xq) = q
0.14
0.12
Fläche: F (xq)
0.1
0.08
0.06
0.04
0.02
0
q-Quantil
q-Quantil
q
x
x
5
10
xq
15
20
0
xq
22
$%9 &
"
Die Zuverlässigkeit (Reliability) wird meist mit der Überlebenswahrscheinlichkeit
(Lebensdauerwahrscheinlichkeit) bezeichnet. Das Gegenteil dazu ist die
Ausfallwahrscheinlichkeit. Der Zusammenhang zwischen der Ausfallrate und der
Lebensdauer lässt sich mit Hilfe der Weibull-Verteilung darstellen. Die Weibull-Verteilung
kann als eine Verallgemeinerung der Exponential-Verteilung angesehen werden. Die
Exponentialverteilung bietet sich als Verteilung von Lebensdauern an, wenn die Ausfallrate
als konstant angesehen wird. Ändert sich dagegen die Ausfallsrate mit der Zeit, so wird die
Verteilung durch die Weibull-Verteilung gegeben.
Weibull-Verteilung
Die Verteilung einer stetigen Zufallsvariable X mit der Dichtefunktion:
0
für
x ≤ 0
f (x) =
,
α ⋅ β ⋅ x β −1 e
− α⋅x β
für
mit
α > 0 und β > 0
x > 0
heißt Weibull-Verteilung.
Die Verteilungsfunktion der Weibull-Verteilung lautet:
0
x
F (x) = P(X ≤ x
) =
f ( u ) du
für
x ≤ 0
=
− ∞
1− e
− α⋅x β
für
x > 0
Für β = 1 ergibt sich aus der Weibull-Verteilung die Exponential-Verteilung.
f ( x)
α =1
β = 4
α =1
β =1
α =1
β = 0,5
α =1
β = 2
x
0
23
Satz
: Erwartungswert und Varianz der Weibull-Verteilung
Der Erwartungswert der Weibull-Verteilung ist:
∞
x ⋅ f ( x ) dx = α
µ =
−
1
β
β +1
⋅Γ
β
− ∞
Die Varianz der Weibull-Verteilung ist:
∞
σ
2
2
f ( x ) ⋅ ( x − µ ) dx = α
=
−
2
β
⋅ Γ
β +2
− ∞
β
− Γ2
β +1
β
- Γ ( α ) gibt die Gamma-Funktion an.
Gamma-Funktion
Die Funktion Γ ( α ) wird als die Gamma-Funktion bezeichnet. Einige Werte der
Gammafunktion können mit Hilfe von Rekursionsformeln berechnet werden. Einige
spezielle Werte und Rekursionsformeln der Gammafunktion sind wie folgt:
Γ
( )=
1
2
Γ(1 ) = 1
π
Γ(α + 1) = α⋅Γ(α)
mit α > 0
Γ(n + 1) = n!
mit n = 1 ; 2 ; 3 ; . . .
(
Γ n +
1
2
)=
( 2 n − 1)
1⋅ 3 ⋅ 5
2n
⋅
π
mit n = 1 ; 2 ; 3 ; . . .
;
Die Lebensdauer X (in Stunden) einer mechanischen Feder sei eine Zufallsgröße, die durch
eine Weibull-Verteilung mit α = 0,1 und β = 0,5 beschrieben wird.
Berechnen Sie
die mittlere Lebensdauer der Feder.
die Wahrscheinlichkeit, dass die Lebensdauer der Feder mehr als 30 Stunden ist.
*+
-
µ = 0 ,1
−
1
0,5
⋅Γ
0,5 + 1
0,5
= 0 , 1 − 2 ⋅ Γ ( 3 ) = 100 ⋅ 2 ! = 200 [ h ]
24
30
P ( X > 30
) = 1 − P ( X ≤ 30 ) = 1 −
= 1−
{
− ∞
0 ⋅ dx +
0
+
= 1 −
0
+
1 –
=
− ∞
0
= 1 −
=
f ( x ) dx
30
0
1
0 ,1 ⋅ 0 , 5 ⋅ x 0 , 5 − 1 e −
− e
1 − e
− 0 , 1⋅ x 0 , 5
0 , 1⋅ x 0 , 5
dx
}
30
0
− 0 , 1 ⋅ 30 0 , 5
−
1 − e
− 0 , 1⋅ 0 0 , 5
{ 0,421 } = 0,578
,
;
Leiten Sie aus der Verteilungsfunktion der Weibull-Verteilung
F(x) = 1 − e
− α ⋅x β
für
x > 0
die Dichtefunktion dieser Verteilung her.
*+
-
,
;
Die Wahrscheinlichkeitsverteilung der Lebensdauer X einer mechanischen Feder aus
Beispiel 2 wurde durch eine Weibull-Verteilung mit α = 0,1 und β = 0,5 gegeben.
Geben Sie mit Hilfe der Verteilungsfunktion die Wahrscheinlichkeit dafür an,
dass die Lebensdauer der Feder mehr als 30 Stunden dauert.
*+
-
25
$%$
*
5
$%$%
*
5
"
Wenn eine Zufallsvariable nicht selbst normalverteilt ist, sondern ihr Logarithmus
normalverteilt ist, so spricht man von einer Lognormalverteilung
Log-Normal-Verteilung
Die Verteilung einer stetigen Zufallsvariable X mit der Dichtefunktion:
0
f (x) =
1
2π β
2
⋅
1
x
⋅ exp −
für
1
ln x − α
2
β
x ≤ 0
,
2
für
mit
β > 0
x > 0
heißt Lognormalverteilung.
Die Verteilungsfunktion der Lognormalverteilung ist:
x
F (x) = P(X ≤ x
) =
x
f ( u ) du =
0
− ∞
1
2π β
2
⋅
1
u
⋅ exp −
1
ln u − α
2
β
2
du
f(x)
α
α
α
β
β
β
x
0
Satz: Erwartungswert und Varianz der Log-Normalverteilung
Der Erwartungswert der Lognormalverteilung ist:
∞
x ⋅ f ( x ) dx = e
µ =
α +
1
2
β2
− ∞
Die Varianz der Lognormalverteilung ist:
∞
σ
2
=
f ( x ) ⋅ ( x − µ ) 2 dx =
eβ
2
− 1
⋅ e 2α
+ β2
− ∞
26
$%$%)
'
&
5
Für eine beliebige log-normalverteilte Zufallsvariable X erhält man durch die Substitution
Y = ln X
eine Zufallsvariable Y , deren Verteilung der Gaußschen-Normalverteilung mit
= β genügt. Analog zu der standardisierten Variable erhält man durch die
Transformation
Y − α
ln X − α
Z =
=
β
= α und
β
eine Zufallsvariable , deren Verteilung der Standard- Normalverteilung gehorcht. Somit
lässt sich die Wahrscheinlichkeit einer log-normalverteilte Zufallsvariable X, für X < x 0,
d.h. P ( X < x 0 ) mit Hilfe der Verteilungsfunktion der Standard- Normalverteilung
bestimmen.
Die folgenden Abbildungen zeigen die graphisch Vorgehensweise zur Bestimmung der
Wahrscheinlichkeit P ( X x0 ) = F (x0 ) einer beliebigen log-normalverteilten
Zufallsvariable X mit Hilfe der Standard-Normalverteilung.
*
5
8
f ( x ) F ( x0 )
f(y)
5
'
5
"
(z)
F ( y0 )
Φ ( z0 )
=
=
0
x0
1
2π β 2
y = ln x
xo
0
1
x
0
x
exp −
dy =
1
ln x − α
2
β
1
x
2π β
z =
z0
0
z
dx
yo
2
y −α
β
y
2
1
dx
y0
α
exp −
−∞
dz =
1
y −α
2
β
1
β
dy
2
dy
1
2π
zo
exp
−∞
−
1
2
z
2
dz
27
Beziehung zur Bestimmung der Wahrscheinlichkeit P ( X x0 ) = F (x0 ) einer
beliebigen log-normalverteilten Zufallsvariable X mit Hilfe der StandardNormalverteilung
Sei x0 eine log-normalverteilte Zufallsvariable, dann lässt sich die Wahrscheinlichkeit
P ( X x0 ) mit Hilfe der Standard-Normal-Verteilung, wie folgt berechnen:
xo
F (xo
)
= P (X ≤ xo
)
1
=
2π β
0
zo
1
=
Dabei ist z o
=
ln x o − α
β
x
⋅ exp −
⋅ exp −
2π
0
⋅
2
1
1
2
z2
1
ln x − α
2
β
2
dz = P ( Z ≤ z o
dx
)=
Φ (zo
)
und µ = α und σ = β sind die Parameter der
Normalverteilung
<
Die Stromausbeute eines bestimmten Transistors wird in Einheiten des Logarithmus
Ia
gemessen, wobei Ia die Ausgangsstromstärke und Ie die Eingangsstromstärke
ln
Ie
angeben. Die Zufallsvariable ln
Ia
ist normalverteilt mit µ = 2 und σ = 0,1.
Ie
Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Quotient
*+
Ia
Ie
geringer als 6,1 ist.
Die Zufallsvariable x =
Ia
Ie
ist log-normalverteilt aber die Zufallsvariable y = ln
Ia
Ie
ist normalverteilt mit µ = 2 und σ = 0,1 daher gilt für die Log-Normalverteilung von X:
α = 2 und β = 0,1.
Es soll die Wahrscheinlichkeit für alle x-Werte kleiner als die obere Grenze x0 = 6,1
berechnet werden. Die Substitution liefert folgende obere Grenze für die Zufallsvariable Z:
zo
=
ln x o − α
β
=
ln 6 , 1 − 2
0 ,1
= −2
Somit erhält man für die gesuchte Wahrscheinlichkeit:
P(X
6,1 ) = P ( Z
– 2 ) = Φ ( – 2 ) = 0,0228
28
$%;
=
3
Die Wahrscheinlichkeit, dass eine Zufallsvariable X zwischen zwei Werten a und b liegt,
kann dann exakt bestimmt werden, wenn die Wahrscheinlichkeitsverteilung bekannt ist. Ist
die Wahrscheinlichkeitsverteilung aber nicht bekannt, so ermöglicht die Tschebyschevsche
Ungleichung eine Abschätzung für die gesuchte Wahrscheinlichkeit P ( a
X
b),
wenn nur der Erwartungswert µ sowie die Standardabweichung σ bekannt sind und für a
bzw. b gilt:
a = µ – c · σ und b = µ + c · σ , wobei c größer als 1 ist.
Tschebyschevsche Ungleichung
Die Wahrscheinlichkeit dafür, dass eine Zufallsvariable X mit dem Erwartungswert
(Mittelwert) µ und Varianz σ 2 innerhalb der c-ten Standardabweichung σ um den
Mittelwert µ liegt, wobei c > 1 ist, beträgt mindestens 1 – 1 c 2 .
P(µ –c·σ
µ +c·σ )
X
1−
1
c2
f(x)
mindestens: 1 –
1
c²
x
c·σ
µ–c·σ
c·σ
µ
µ+c·σ
Die Tschebyschevsche Ungleichung gilt sowohl für stetige als auch für diskrete
Zufallsvariablen.
,
<
Die Lebensdauer X (in Stunden) von seriengefertigten Halogenlampen sei eine
Zufallsvariable mit einem Mittelwert von 800 [h] und einer Standardabweichung von 40 [h].
Wie groß ist mindestens der Anteil der hergestellten Lampen mit einer Lebensdauer
zwischen 740 [h] und 860 [h]?
*+
a
= 740 [h] ; b
a =
µ – c·σ
740 = 800 – c · 40
P(a
X
=
;
µ = 800 [h] ;
bzw.
⇔
σ =
b
=
µ
+ c·σ
c =
b )
29