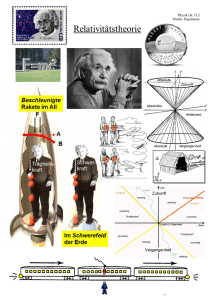
Überlegungen zur Relativitätstheorie

Überlegungen zur Relativitätstheorie
In gleichförmig bewegten Systemen laufen alle physikalischen Vorgänge gleich schnell ab!
Beispiel: Ein Zug fährt mit 80 km/h. Ein Passagier geht mit einer Geschwindigkeit von 5 km/h vom
letzten bis zum 1. Waggon.
Für einen Beobachter am Bahngleis bewegt sich der Passagier mit 85 km/h (80 + 5).
D.h. obwohl die Geschwindigkeit innerhalb des Zuges genauso groß wäre, wie außerhalb des
Zuges, erscheint es dem außen Stehenden anders.
Diese Überlegung gilt auch für das Licht. Ein Lichtstrahl vom letzten bis zum 1. Waggon eines 1
km langen Zuges würde etwa 3,3* 10-6 sec (0,0000033 Sekunden) benötigen. Im Zug bewegt sich
das Licht genau so schnell wie in jedem anderen System, also mit
300 000 km/sec.
Für einen Beobachter von außen kommt allerdings die Geschwindigkeit des Zuges noch hinzu. Das
sind bei einem Zug der 80 km/h fährt noch mal 0,022 km pro Sekunde. Die Lichtgeschwindigkeit
beträgt also für den externen Beobachter 300 000 km + 0,022 km pro Sekunde. Man kann dieses auf
relativ einfach Weise mit Hilfe des Satzes von Pythagoras nachweisen.
Wenn nun alle physikalischen Vorgänge innerhalb und außerhalb des Zuges gleich schnell
ablaufen, physikalische Vorgänge im Zug aber von außen betrachtet schneller ablaufen (weil das
Licht bzw. der Passagier sich schneller bewegen um zum 1. Waggon zu kommen), so muss das
auch für die Zeit gelten. Die Zeit scheint von außen betrachtet schneller zu vergehen als im Zug
selbst.
Einstein hat dazu einen sogenannten Zeitstreckungsfaktor (hier z genannt) errechnet, der angibt,
um welchen Faktor die Zeit außerhalb des Zuges schneller vergeht als innerhalb des Zuges.
v = Geschwindigkeit des Zuges
1
z 
v
c = Lichtgeschwindigkeit (ca. 300 000 km/sec)
1 ( )
2
c
Beispiel: der Zug fährt mit 50 % Lichtgeschwindigkeit:
1
Dann gilt z 
 1,1547
1 (
1 2
)
2
Wenn im Zug eine Stunde vergeht, vergehen außerhalb etwa 69,28 Minuten.
Je näher die Geschwindigkeit des Zuges der Lichtgeschwindigkeit kommt, desto größer wird der
Zeitstreckungsfaktor.
Allerdings: Der Lichtstrahl einer Taschenlampe ist innerhalb des Zuges genau so schnell wie von
außen betrachtet, nämlich ca. 300 000 km/sec. Es gibt nichts, was schneller sein kein als das Licht.
Das ist nach dem vorher gesagten paradox, ist aber die Grundlage der Relativitätstheorie.
Zu den Fragen:
a) Bei 90 % Lichtgeschwindigkeit wäre
b) Bei 99% Lichtgeschwindigkeit wäre
c) Bei 99,999 % Lichtgeschwindigkeit wäre
z = 2,294
z = 7,088
z = 223,6
Uhrzeit am Bahnhof 14: 17
Uhrzeit am Bahnhof 19:05
Es wären mehr als 9 Tage
vergangen
d) Hiermit kann bewiesen werden, dass nichts schneller sein kann als das Licht. Mathematisch
gesehen, darf der Zähler niemals größer werden als der Nenner, er darf auch nicht gleich
groß werden, da sonst der gesamte Nenner den Wert Null hat. Und dies darf nicht sein!
Wenn der Zug tatsächlich so schnell wäre, würde es vielleicht einen großen Knall geben
und das Universum würde neu entstehen oder so was in der Richtung.