(Verbrauchsmaterial) (Word Datei, 334 kB)

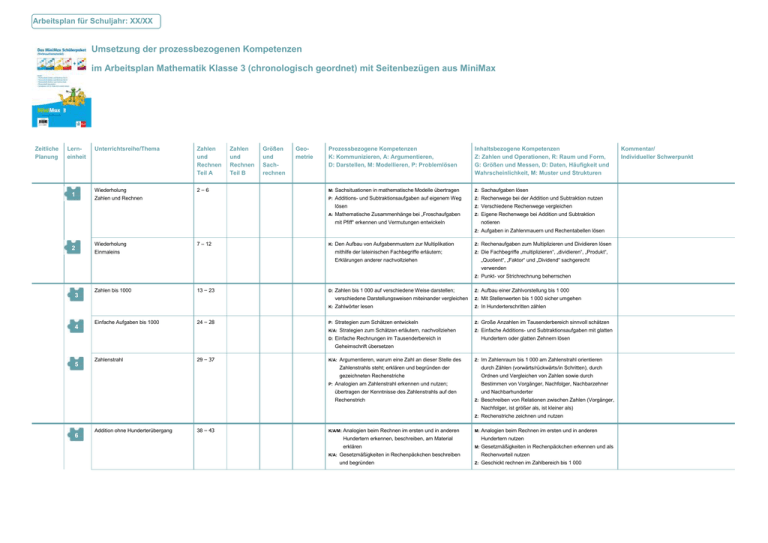
Arbeitsplan für Schuljahr: XX/XX
Umsetzung der prozessbezogenen Kompetenzen
im Arbeitsplan Mathematik Klasse 3 (chronologisch geordnet) mit Seitenbezügen aus MiniMax
Zeitliche
Planung
Lerneinheit
1
Unterrichtsreihe/Thema
Zahlen
und
Rechnen
Teil A
Wiederholung
2–6
Zahlen und Rechnen
Zahlen
und
Rechnen
Teil B
Größen
und
Sachrechnen
Geometrie
Prozessbezogene Kompetenzen
K: Kommunizieren, A: Argumentieren,
D: Darstellen, M: Modellieren, P: Problemlösen
Inhaltsbezogene Kompetenzen
Z: Zahlen und Operationen, R: Raum und Form,
G: Größen und Messen, D: Daten, Häufigkeit und
Wahrscheinlichkeit, M: Muster und Strukturen
M:
Sachsituationen in mathematische Modelle übertragen
Z:
Sachaufgaben lösen
P:
Additions- und Subtraktionsaufgaben auf eigenem Weg
Z:
Rechenwege bei der Addition und Subtraktion nutzen
lösen
Z:
Verschiedene Rechenwege vergleichen
Mathematische Zusammenhänge bei „Froschaufgaben
Z:
Eigene Rechenwege bei Addition und Subtraktion
A:
mit Pfiff“ erkennen und Vermutungen entwickeln
2
Wiederholung
7 – 12
K:
Einmaleins
notieren
Z:
Aufgaben in Zahlenmauern und Rechentabellen lösen
Den Aufbau von Aufgabenmustern zur Multiplikation
Z:
Rechenaufgaben zum Multiplizieren und Dividieren lösen
mithilfe der lateinischen Fachbegriffe erläutern;
Z:
Die Fachbegriffe „multiplizieren“, „dividieren“, „Produkt“,
„Quotient“, „Faktor“ und „Dividend“ sachgerecht
Erklärungen anderer nachvollziehen
verwenden
3
4
Zahlen bis 1000
Einfache Aufgaben bis 1000
13 – 23
24 – 28
Z:
Punkt- vor Strichrechnung beherrschen
Zahlen bis 1 000 auf verschiedene Weise darstellen;
Z:
Aufbau einer Zahlvorstellung bis 1 000
verschiedene Darstellungsweisen miteinander vergleichen
Z:
Mit Stellenwerten bis 1 000 sicher umgehen
K:
Zahlwörter lesen
Z:
In Hunderterschritten zählen
P:
Strategien zum Schätzen entwickeln
Z:
Große Anzahlen im Tausenderbereich sinnvoll schätzen
Z:
Einfache Additions- und Subtraktionsaufgaben mit glatten
D:
K/A:
D:
Strategien zum Schätzen erläutern, nachvollziehen
Einfache Rechnungen im Tausenderbereich in
Hundertern oder glatten Zehnern lösen
Geheimschrift übersetzen
5
Zahlenstrahl
29 – 37
K/A:
P:
Argumentieren, warum eine Zahl an dieser Stelle des
Z:
Im Zahlenraum bis 1 000 am Zahlenstrahl orientieren
Zahlenstrahls steht; erklären und begründen der
durch Zählen (vorwärts/rückwärts/in Schritten), durch
gezeichneten Rechenstriche
Ordnen und Vergleichen von Zahlen sowie durch
Analogien am Zahlenstrahl erkennen und nutzen;
Bestimmen von Vorgänger, Nachfolger, Nachbarzehner
übertragen der Kenntnisse des Zahlenstrahls auf den
Rechenstrich
und Nachbarhunderter
Z:
Beschreiben von Relationen zwischen Zahlen (Vorgänger,
Nachfolger, ist größer als, ist kleiner als)
6
Addition ohne Hunderterübergang
38 – 43
K/A/M:
Analogien beim Rechnen im ersten und in anderen
Z:
Rechenstriche zeichnen und nutzen
M:
Analogien beim Rechnen im ersten und in anderen
Hundertern erkennen, beschreiben, am Material
erklären
K/A:
Hundertern nutzen
M:
Gesetzmäßigkeiten in Rechenpäckchen beschreiben
und begründen
Gesetzmäßigkeiten in Rechenpäckchen erkennen und als
Rechenvorteil nutzen
Z:
Geschickt rechnen im Zahlbereich bis 1 000
Kommentar/
Individueller Schwerpunkt
Arbeitsplan für Schuljahr: XX/XX
Zeitliche
Planung
Lerneinheit
7
Unterrichtsreihe/Thema
Zahlen
und
Rechnen
Teil A
Addition mit Hunderterübergang
44 – 52
Zahlen
und
Rechnen
Teil B
Größen
und
Sachrechnen
Geometrie
Prozessbezogene Kompetenzen
K: Kommunizieren, A: Argumentieren,
D: Darstellen, M: Modellieren, P: Problemlösen
D/K:
Rechenstrich als halbschriftliche Rechenstrategie und
Inhaltsbezogene Kompetenzen
Z: Zahlen und Operationen, R: Raum und Form,
G: Größen und Messen, D: Daten, Häufigkeit und
Wahrscheinlichkeit, M: Muster und Strukturen
Z:
als Veranschaulichung des Rechenweges nutzen
K/A:
Rechenwege erklären und begründen
Konkrete Vorstellungen von Stellenwerten und der
Zehnerbündelung für die Addition nutzen.
Z:
Analogien in allen Hundertern nutzen
Z:
Halbschriftliches Rechnen als Dokumentation des
Rechenweges und als Hilfe anwenden
8
Additionsaufgaben üben
53 – 57
D/K:
Rechenstrich als halbschriftliche Rechenstrategie und
Z:
Hundertertrick anwenden
Z:
Rechenwege vergleichen und bewerten
Z:
Gleichungsschreibweise und Rechenstrich für die Addition
als Veranschaulichung des Rechenweges nutzen
K/A:
Rechenwege erklären und begründen, Fehler finden
nutzen
Z:
Hundertertrick anwenden
Z:
Geeigneten Rechenweg, im Kopf oder halbschriftlich,
erkennen und nutzen
43
2–3
Wiederholung
A:
Geometrie
Mit unterschiedlichen Eigenschaften der Körper
Z:
Rechenfehler finden, erklären und korrigieren
R:
Eigenschaften von Würfel, Quader und Kugel kennen und
argumentieren
Körper danach sortieren
K:
Lösungsstrategien beschreiben
R:
Zuordnen von Ansichten zu Gebilden
D:
Baupläne von Würfelgebäuden lesen und zuordnen
R:
Zweidimensionale Darstellungen von Würfelgebäuden
zueinander in Beziehung setzen
44
4–7
Geometrische Körper
A:
Begründen, warum sich von einigen Körpern keine
R:
Symmetrische Muster fortsetzen
R:
Eigenschaften der Achsensymmetrie nutzen
R:
Körper (auch in der Umwelt) wiedererkennen und
Kantenmodelle bauen lassen
K:
Ergebnisse der Untersuchung der Körpereigenschaften
benennen
R:
präsentieren
A:
45
46
8 – 11
Würfelnetze
12 – 15
Würfelgebäude
P:
Eigenschaften der Körper (Anzahl Flächen, Kanten und
Ecken) kennen
Aussage, woran ein Körper besonders gut erkannt wird,
R:
Körpern Netze zuordnen
begründen; mit Aussagen anderer vergleichen
R:
Modelle von Körpern herstellen
Finden von verschiedenen Würfelnetzen und Überprüfen
R:
Finden und Überprüfen von verschiedenen Würfelnetzen
auf Richtigkeit
R:
Würfelnetze durch gedankliches Spiegeln und Drehen
A:
Begründen, warum ein Netz kein Würfelnetz ist
K:
Austausch über die gefundenen Würfelnetze und
R:
Würfel und Netz einander zuordnen
Überprüfen der Netze auf doppelte Lösungen
R:
Räumliches Vorstellungsvermögen nutzen
Ordnungskriterien beschreiben und Zuordnungen
R:
Zweidimensionale Darstellungen von Würfelgebäuden
A:
aufeinander abbilden
begründen (Baupläne, Baupläne und Ansichten)
M:
zueinander in Beziehung setzen (zu Würfelgebäuden
Zwischen verschieden Darstellungsformen wechseln
Baupläne erstellen, Modelle untersuchen)
R:
Anzahl der Würfel von Würfelgebäuden bzw. Anzahl zu
einem Quader fehlender Würfel bestimmen
9
Subtraktion ohne Hunderterübergang
58 – 63
K/A/M:
Analogien beim Rechnen im ersten und in anderen
Z:
Hundertern erkennen, beschreiben, am Material
erklären
K/A:
Hundertern nutzen
M:
Gesetzmäßigkeiten in Rechenpäckchen beschreiben
und begründen
Analogien beim Rechnen im ersten und in anderen
Gesetzmäßigkeiten in Rechenpäckchen erkennen und als
Rechenvorteil nutzen
Z:
Geschickt rechnen im Zahlbereich bis 1 000
Kommentar/
Individueller Schwerpunkt
Arbeitsplan für Schuljahr: XX/XX
Zeitliche
Planung
Lerneinheit
10
Unterrichtsreihe/Thema
Zahlen
und
Rechnen
Teil A
Subtraktion mit Hunderterübergang
64 – 71
Zahlen
und
Rechnen
Teil B
Größen
und
Sachrechnen
Geometrie
Prozessbezogene Kompetenzen
K: Kommunizieren, A: Argumentieren,
D: Darstellen, M: Modellieren, P: Problemlösen
D/K:
K/A:
11
Subtraktionsaufgaben üben
72 – 75
D/K:
K/A:
Inhaltsbezogene Kompetenzen
Z: Zahlen und Operationen, R: Raum und Form,
G: Größen und Messen, D: Daten, Häufigkeit und
Wahrscheinlichkeit, M: Muster und Strukturen
Rechenstrich als halbschriftliche Rechenstrategie und
Z:
Analogien in allen Hundertern nutzen
als Veranschaulichung des Rechenweges nutzen
Z:
Rechnungen halbschriftlich mit Gleichungen oder
Rechenwege erklären und begründen
Rechenstrich dokumentieren
Z:
Hundertertrick anwenden
Z:
Differenz durch Ergänzen ermitteln
Z:
Verschiedene Rechenwege vergleichen und bewerten
Rechenstrich als halbschriftliche Rechenstrategie und
Z:
Umkehraufgaben für Aufgaben mit Platzhaltern nutzen
als Veranschaulichung des Rechenweges nutzen
Z:
Umkehraufgaben als Probe nutzen
Rechenwege erklären und begründen, Fehler finden
Z:
Geeigneten Rechenweg, im Kopf oder halbschriftlich,
erkennen und nutzen
M:
Systematische Veränderungen in Aufgabenpäckchen
nachvollziehen und ggf. erklären
12
Sachrechengeschichten
76 – 80
Z:
Rechenfehler finden, erklären und korrigieren
Informationen aus Sachtexten in Zeichnungen, Tabellen
D:
Passende Informationen in einem Sachtext unterstreichen
und/oder Rechnungen übertragen
D:
Informationen aus einem Sachtext für Aufgaben nutzen
P:
Sinnvollste Lösungsstrategie entwickeln und nutzen
Z:
Überschlag bei Sachaufgaben anwenden
A:
Vermutungen aufstellen, überprüfen und belegen
Z:
Eigene Lösungswege finden und passende Antworten
M:
notieren
Z:
Behauptungen durch verschiedene Lösungs-wege
überprüfen
13
Kombinatorik
81 – 84
P:
Kombinatorische Fragestellungen lösen
K/A:
Z:
Sich darüber austauschen, wann man eine Tabelle
Kombinatorische Fragestellungen über das Anlegen eines
Baumdiagrams oder einer Tabelle lösen
anlegen kann und wann nicht
M:
Probleme aus einer Sachsituation heraus in eine
kombinatorische Fragestellung übertragen und mit Hilfe
eines Baumdiagramms oder einer Tabelle lösen
14
Daten, Zufall und Wahrscheinlichkeit
85 – 88
P:
Mathematische Kenntnisse beim Zeichnen von
D:
A:
Mathematische Zusammenhänge erkennen und
Vermutungen beim Urnenmodell entwickeln
Begriffe „sicher“, „immer“ „möglich“, häufig“, „selten“,
„unmöglich“ und nie kennen und zur Einschätzungen von
Glücksrädern anwenden
Wahrscheinlichkeiten nutzen
D:
Gewinnchancen bei Glücksrädern und Urnen einschätzen
Mathematische Fachbegriffe und Zeichen sachgerecht
G:
Mit cm und m rechnen, dabei nutzen, dass 1 m = 100 cm
verwenden
G:
Geldwerte notieren und vergleichen
A:
Zuordnung von Preisen begründen
G:
Preise zuordnen
P:
Faustregel zur Bestimmung der Anzahl der Tage eines
G:
Bestimmte Anzahl von Tagen den Monaten zuordnen
Monats nutzen; Uhrzeiten auch bei knapper beschrifteten
G:
Uhrzeiten ablesen und Zeitspannen berechnen
K:
Eigene Vorgehensweise beim Zeichnen von Glücksrädern
und Urnen beschreiben, Lösungswege anderer verstehen
und gemeinsam darüber reflektieren
31
Wiederholung Größen und Sachrechnen
2 –3
K:
Ziffernblatt ablesen; mathematische Kenntnisse bei der
Berechnung von Zeitspannen anwenden
32
Geld
4–9
K:
Geldbeträge mit Komma lesen
G:
Alle Euromünzen und -scheine und Centmünzen kennen
D:
Geldbeträge mit Komma schreiben
G:
Geldbeträge ermitteln
P:
Geldbeträge halbieren und verdoppeln
G:
Geldbeträge der Größe nach sortieren, ver-gleichen,
verdoppeln, halbieren, ergänzen
G:
Geldbeträge unterschiedlich darstellen
Kommentar/
Individueller Schwerpunkt
Arbeitsplan für Schuljahr: XX/XX
Zeitliche
Planung
Lerneinheit
47
Unterrichtsreihe/Thema
Zahlen
und
Rechnen
Teil A
Zahlen
und
Rechnen
Teil B
Wegepläne
Größen
und
Sachrechnen
Geometrie
Prozessbezogene Kompetenzen
K: Kommunizieren, A: Argumentieren,
D: Darstellen, M: Modellieren, P: Problemlösen
16 –18
D:
Koordinaten/Symbole auf einem (Wege-)Plan angeben,
Inhaltsbezogene Kompetenzen
Z: Zahlen und Operationen, R: Raum und Form,
G: Größen und Messen, D: Daten, Häufigkeit und
Wahrscheinlichkeit, M: Muster und Strukturen
R:
ablesen und/oder einzeichnen
K:
Wegstrecken beschreiben und Beschreibungen
angeben/eintragen
R:
nachvollziehen
A:
Koordinaten aus dem Wegeplan ablesen und
Wege planen und beschreiben (an der 1.  Kreuzung
rechts, an der 3. Kreuzung links, geradeaus)
Wegstrecke begründen („Ich wähle diesen Weg, weil er z.
B. der kürzere ist.“)
48
19 –24
Geodreieck
D:
R:
Quadrat, Parallelogramm
A:
49
Konstruktion von Senkrechten, Parallelen, Rechteck,
25 –27
Flächen auslegen
Geometrische Flächen erkennen und benennen: Viereck,
Rechteck, Quadrat, Parallelogramm, Dreieck
Begründen, warum Rechtecke und Quadrate auch
R:
Faltanleitungen umsetzen
Parallelogramme sind
R:
Mit dem Geodreieck zeichnen
R:
Bestimmen und Vergleichen von Flächeninhalten durch
K/A:
Austauschen über geschicktes Ausrechnen von
Flächeninhalten
das Auslegen mit Einheitsquadraten bzw. (geschicktes)
Berechnen der Summe Einheitsquadrate
50
28 –30
Muster und Parkettieren
K:
Regeln für das Fortsetzen von geometrischen und
R:
Erkennen der Flächeninvarianz
M:
Gesetzmäßigkeiten in Mustern erkennen, beschreiben
anderen Mustern (z. B. in Bildern) nennen
P:
M:
und Muster fortsetzen
Strukturen in Mustern erkennen und für das Fortsetzen
M:
Fehlende Teile im Muster ersetzen
und die eigene Entwicklung von Mustern nutzen
M:
Parkettieren mit geometrischen Formen als weitere
Darstellung von „Mustern“ begreifen und Parkettierungen
Aus vorgegebenen Formen Parkette legen
durchführen
M:
Verschiedene Möglichkeiten der Parkettierung mit
vorgegebenen Formen diskutieren, legen und zeichnen
51
31 –33
Symmetrie
K:
P:
Strategie beim Erstellen symmetrischer Figuren
R:
Ebene Figuren auf Symmetrie überprüfen.
beschreiben
R:
Ebene Figuren symmetrisch in Gitternetzen zeichnen und
Erkennen von Spiegelbildern anwenden
M:
ergänzen – horizontal, vertikal
Geometrische Kenntnisse bei der Erstellung und beim
R:
Den Spiegel als Hilfsmittel zum Erkennen gespiegelter
Eigenschaften der Achsensymmetrie erkennen,
beschreiben und nutzen
Formen an der Symmetrieachse einsetzen
15
Zehnereinmaleins
2–9
K/A: Rechenwege
erläutern und die anderer Kinder
nachvollziehen
K:
Aufgaben des Zehnereinmaleins lösen
Z:
Divisionsaufgaben als Umkehraufgaben des
Mathematische Fachbegriffe „Vielfache“ und „Teiler“
sachgerecht verwenden
P:
Z:
Zehnereinmaleins lösen
Z:
Alle 4 Aufgaben einer Aufgabenfamilie finden;
Begriffe „Vielfache“ und „Teiler“ kennen lernen und
sachgerecht verwenden
Zusammenhänge beim Rechnen mit 10 und 100 erkennen
16
Halbschriftliche Multiplikation
10 – 15
K/A:
Z:
Multiplikationsaufgaben vorstellen und nachvollziehen
16 – 20
multiplizieren
Z:
Halbschriftliche Multiplikation verstehen und anwenden
festhalten (in Tabellen, in halbschriftlicher Notation)
Z:
Rechenschritte notieren
Gemeinsamkeiten bei Ergebnissen erkennen und
Z:
In Tabellen schrittweise multiplizieren
begründen
Z:
Verschiedene Rechenwege vergleichen und begründen
D:
Rechenschritte der Division schriftlich festhalten
Z:
Mehrstellige Zahlen in Schritten ohne Rest durch
A:
Aufgabenmuster erläutern
A:
Halbschriftliche Division
Einstellige mit zweistelligen Zahlen in Schritten
Rechenschritte der Multiplikation auf verschiedene Weise
D:
17
Rechenwege zum Lösen halbschriftlicher
einstellige Zahlen dividieren
Z:
Halbschriftliche Division verstehen und anwenden
Z:
Rechenschritte notieren
Z:
Multiplikative Umkehraufgabe als Rechenprobe nutzen
Kommentar/
Individueller Schwerpunkt
Arbeitsplan für Schuljahr: XX/XX
Zeitliche
Planung
Lerneinheit
18
Unterrichtsreihe/Thema
Halbschriftliche Division mit Rest
Zahlen
und
Rechnen
Teil A
Zahlen
und
Rechnen
Teil B
Größen
und
Sachrechnen
21 – 23
Geometrie
Prozessbezogene Kompetenzen
K: Kommunizieren, A: Argumentieren,
D: Darstellen, M: Modellieren, P: Problemlösen
P/A:
Durch Vergleichen der Einerziffern erkennen, wann eine
Inhaltsbezogene Kompetenzen
Z: Zahlen und Operationen, R: Raum und Form,
G: Größen und Messen, D: Daten, Häufigkeit und
Wahrscheinlichkeit, M: Muster und Strukturen
Z:
Zahl durch 2, 5, oder 10 teilbar ist, und dies erläutern
Mehrstellige Zahlen in Schritten mit Rest durch einstellige
Zahlen dividieren
Z:
Halbschriftliche Division mit Rest verstehen und
anwenden
Z:
Rechenschritte notieren
Z:
Die multiplikative Umkehraufgabe mit anschließender Addition als Rechenprobe nutzen
19
Verdoppeln und Halbieren
24 – 26
Z:
Große Zahlen bis 500 verdoppeln
Z:
Große Zahlen bis 1 000 halbieren
Fehlende Zahlen in Aufgabenfamilien finden;
Z:
Halbschriftliche Multiplikationsaufgaben lösen
Verdopplungen und Halbierungen von Aufgabenfamilien
Z:
Halbschriftliche Divisionsaufgaben mit und ohne Rest
A/K:
P:
Sich über Rechenschritte austauschen
Zahlenrätsel in Rechnungen übersetzen, um eine
gesuchte Zahl zu ermitteln
20
Multiplikation und Division üben
27 – 30
P:
erkennen; Regelmäßigkeiten in Aufgabenmustern
erkennen
A/K:
lösen
Z:
Sich über Entdeckungen bei Aufgabenfamilien und
Aufgabenfamilien zu Multiplikations- und
Divisionsaufgaben bilden
Aufgabenmustern austauschen
21
Sachrechnen
31 – 33
M:
Sachsituationen in Rechnungen übertragen, Rechnungen
Z:
lösen und Lösungen auf die Sachsituation beziehen
P:
Für sich einen passenden Lösungsweg finden
Zu einer Sachsituation eine passende Rechenoperation
finden
Z:
Sachaufgaben mit Hilfe der Multiplikation und Division
lösen
Z:
Passende Fragen und Antworten zu einer Sachsituation
formulieren
22
33
Gleichungen und Ungleichungen
Rechnen mit -Kommazahlen
34 – 38
Lösungsstrategien beim Finden von passenden Zahlen
Z:
Angemessene Überschläge bilden
entwickeln und nutzen; Überschlag geschickt einsetzen
Z:
Überschlag bei Relationen anwenden
K:
Mathematische Zeichen <, =, > sachgerecht verwenden
Z:
Zahlen und Aufgaben bzw. Aufgaben zuein-ander in
A:
Mathematische Zusammenhänge im Zahlenraum bis 1
P:
10 – 11
P:
000 durch Finden größt- oder kleinstmöglicher Zahlen
Z:
Relationszeichen (<,>, =) setzen
erkennen und begründen
Z:
Relationen durch Einsetzen von Zahlen ergänzen
Mathematische Kenntnisse bei der Bearbeitung
G:
Geldbeträge in unterschiedliche Schreibweisen
problemhaltiger Aufgaben anwenden
D:
34
Beziehung setzen
Sachrechnen mit Geld
12 – 14
M:
Geldbeträge in unterschiedlicher Schreibweise darstellen
umwandeln
G:
Geldbeträge addieren und subtrahieren
G:
Geldbeträge multiplizieren und dividieren
Sachsituationen erfassen und mit Skizze, Tabelle oder
G:
Sachaufgaben mit der Größe Geld lösen
Rechnung lösen
G:
Passende Fragen formulieren
P:
Für sich einen passenden Lösungsweg finden
G:
Eigene Lösungswege notieren
A:
Begründen, warum bestimmte Kartenpreise
G:
Längen mit Messgeräten messen und zeichnen, dabei die
günstiger/teurer sind
35
Längen
15 – 24
P:
Verschiedene Längen mit dem jeweils geeigneten
Messgerät messen
D:
Einheiten mm, cm, m und km sachgerecht anwenden
Ergebnisse der Addition und Subtraktion von kleinen
G:
Größenvorstellungen zu Längen entwickeln
Längen durch Kontrollzeichnungen überprüfen
G:
Rechnen mit mm, cm, m und km
G:
Umwandeln von Größen mit der Kommaschreibweise bei
K/P:
Rechenweg beim Addieren von Längen mit Übertrag
beschreiben, auf Subtraktion übertragen
m und cm
G:
Alltagsbruch ½ auf Längen anwenden
Kommentar/
Individueller Schwerpunkt
Arbeitsplan für Schuljahr: XX/XX
Zeitliche
Planung
Lerneinheit
36
Unterrichtsreihe/Thema
Zahlen
und
Rechnen
Teil A
Zahlen
und
Rechnen
Teil B
Größen
und
Sachrechnen
25 – 27
Sachrechnen mit Längen
Geometrie
Prozessbezogene Kompetenzen
K: Kommunizieren, A: Argumentieren,
D: Darstellen, M: Modellieren, P: Problemlösen
Inhaltsbezogene Kompetenzen
Z: Zahlen und Operationen, R: Raum und Form,
G: Größen und Messen, D: Daten, Häufigkeit und
Wahrscheinlichkeit, M: Muster und Strukturen
D:
Informationen in Skizzen übertragen
P:
Für sich entdecken, welche Lösungsstrategie die
Kommaschreibweise (m, cm) im Kopf oder halbschriftlich
sinnvollste ist
durch Umwandeln
Z:
Subtrahieren und Addieren von Längen in
Z:
Sachaufgaben mit Längenangaben lösen
Z:
Informationen aus Skizzen entnehmen und für Aufgaben
nutzen
37
28 – 36
Zeit
P:
Zusammenhänge erkennen und auf ähnliche
Z:
Eigene Lösungswege finden
G:
Stunden, Minuten und Sekunden als Einheiten der Zeit
Sachverhalte übertragen
K:
M:
kennen
Verschiedene Sprechweisen zur Uhrzeit verstehen und
G:
Zeitspannen ergänzen und umwandeln
nutzen
G:
Uhrzeiten minutengenau ablesen und einstellen
Fahrplänen die relevanten Informationen entnehmen und
G:
Analoge und digitale Zeitangaben zueinander in
damit Fragen beantworten
Beziehung setzen
G:
Einfache Bruchzahlen im Zusammenhang mit Zeit kennen
und verstehen
38
37 – 38
Das Jahr
K:
Kalender sachgerecht verwenden; eigene
G:
Vorgehensweisen beschreiben, Lösungswege anderer
D:
nutzen
verstehen und gemeinsam darüber reflektieren
G:
Besondere Tage in einem Kalender erkennen
Eine Darstellung in eine andere Übertragen: verschiedene
G:
Kalender zur Bestimmung des Wochentags eines Datums
Sprech- und Schreibweisen nutzen
23
Schriftliche Addition
39 – 40
D:
Mit Material die Addition größerer Zahlen legen und
nutzen
Z:
nachvollziehen
A:
Jahr, Monat und Tag als Einheiten der Zeit kennen und
Schriftliche Rechenverfahren der Addition kennen und
sicher ausführen
Mathematische Zusammenhänge beim schriftlichen
Addieren erkennen und Vorgänge beim Legen mit
Material verbalisieren
24
Schriftliche Addition üben
41 – 47
D:
P:
25
Schriftliche Subtraktion
48/49
D:
Mit Material die Addition von drei Zahlen legen und
Z:
Schriftliches Additionsverfahren kennen und nutzen
nachvollziehen
Z:
Schriftliche Addition an bekannten Aufgabenmustern
Mathematische Kenntnisse bei der Bearbeitung
anwenden
problemhaltiger Aufgaben anwenden; Lösungsstrate-gien
Z:
Rechenfehler finden und korrigieren
wie systematisches Kombinieren nutzen
Z:
Rechnungen durch Überschlag überprüfen
Z:
Schriftliche Addition mit drei Summanden anwenden
Z:
Schriftliche Rechenverfahren der Subtraktion kennen und
Mit Material die Subtraktion größerer Zahlen legen und
nachvollziehen
A:
sicher ausführen
Mathematische Zusammenhänge beim schriftlichen
Subtrahieren erkennen und Vorgänge beim Legen mit
Material verbalisieren
26
Schriftliche Subtraktion üben
50 – 56
P:
Mathematische Kenntnisse bei der Bearbeitung
Z:
Schriftliches Subtraktionsverfahren kennen und nutzen
problemhaltiger Aufgaben anwenden
Z:
Schriftliche Subtraktion an bekannten Aufgabenmustern
anwenden
27
Aufgaben kontrollieren
57 – 58
Z:
Rechenfehler finden und korrigieren
Z:
Rechnungen durch Überschlag überprüfen
K:
Ergebnisse vergleichen
Z:
Rechenfehler finden, erklären und korrigieren
A:
Richtige/falsche Ergebnisse begründen
Z:
Umkehraufgaben bilden und zur Kontrolle von
Ergebnissen nutzen (Probe durchführen)
Z:
Überschläge bilden und zur Kontrolle von Ergebnissen
nutzen
Kommentar/
Individueller Schwerpunkt
Arbeitsplan für Schuljahr: XX/XX
Zeitliche
Planung
Lerneinheit
28
Unterrichtsreihe/Thema
Sachrechnen (Projekte)
Zahlen
und
Rechnen
Teil A
Zahlen
und
Rechnen
Teil B
Größen
und
Sachrechnen
59 – 63
Geometrie
Prozessbezogene Kompetenzen
K: Kommunizieren, A: Argumentieren,
D: Darstellen, M: Modellieren, P: Problemlösen
M:
Sachtexten, Tabellen und Fahrplänen relevante
D:
Informationen entnehmen; Sachsituationen in
Zeichnungen, Tabellen und Rechnungen übertragen
A/M:
P:
29
Inhaltsbezogene Kompetenzen
Z: Zahlen und Operationen, R: Raum und Form,
G: Größen und Messen, D: Daten, Häufigkeit und
Wahrscheinlichkeit, M: Muster und Strukturen
Tabellen und Diagramme
64 – 67
K:
Antworten aus dem Sachzusammenhang begründen
Informationstexten finden und nutzen
Z:
Sachaufgaben lösen
Z:
Eigene Lösungswege finden und passende Antworten
Lösungsstrategien entwickeln
Über die Daten eines Diagramms austauschen;
notieren
Z:
Kleine Projekte eigenständig planen
D:
Daten aus Tabellen entnehmen und in ein Diagramm
Fachbegriffe verwenden
D:
A:
übertragen
Daten in einem Diagramm darstellen; Darstellungen von
Z:
Fachbegriffe nutzen
Daten miteinander vergleichen und bewerten
D:
Informationen aus einem Diagramm ablesen
Daten eines oder mehrerer Diagramme vergleichen und
D:
Daten sammeln und in Tabellen und Diagrammen
Aussagen dazu treffen
M:
Informationen in Rezepten, Tabellen und
darstellen
Tabellen und Diagrammen Informationen entnehmen und
diese zur Beantwortung von Fragen nutzen
30
Rechenvorteile
68 – 70
K:
Eigene Vorgehensweise beschreiben, Lösungswege
Z:
anderer verstehen und darüber reflektieren
P:
Lösungsstrategie entwickeln und nutzen
Zahlbeziehungen erkennen und für geschicktes Rechnen
nutzen
Z:
Verdopplungsaufgaben,
Z:
Partnerzahlen, Tauschaufgaben, 10er/100er-Trick
erkennen und nutzen
39
Gewichte
39 – 45
P:
Verschiedene Gegenstände mit der jeweils geeigneten
G:
Waage wiegen
A:
Argumentieren, warum es nötig ist, mit standardisierten
ordnen, Gewichte schätzen
G:
Maßen zu wiegen
K:
Aufgaben gemeinsam bearbeiten
Gewicht von Gegenständen vergleichen, nach Gewicht
Maßeinheiten Gramm, Kilogramm und Tonne sachgerecht
anwenden
G:
Größenvorstellungen zu g, kg und t entwickeln,
Stützpunktwissen aufbauen
G:
Gegenstände mit geeigneten Waagen wiegen
G:
Einfache Bruchzahlen im Zusammenhang mit Gewicht
kennen und verstehen
40
Sachrechnen mit Gewichten
46 – 47
Sachsituationen in Tabellen und/oder Rechnungen
D:
übertragen
P:
G:
Sachaufgaben mit Gewichtsangaben lösen
Z:
Eigene Lösungswege finden und passende Antworten
Für sich entdecken, welche Lösungsstrategie die
sinnvollste ist
K/A:
Argumentieren, warum dies ein möglicher Lösungsweg
notieren
G:
Informationen aus einem Rezept für Aufgaben nutzen
G:
Gewichtsangaben für andere Personenzahlen abändern
G:
Geldbeträge, Längenmaße mit Kommaschreibweise
ist
41
Schriftlich rechnen mit Kommazahlen
48 – 51
P:
Zusammenhänge zum schriftlichen Addieren und
Subtrahieren nutzen
K:
A:
schriftlich addieren und subtrahieren
Kommazahlen sachgerecht schreiben, um addieren und
G:
Lösungen durch Überschlagsrechnungen kontrollieren
subtrahieren zu können
G:
Größen umwandeln, um diese addieren und subtrahieren
Argumentieren, wie bei unterschiedlichen Einheiten
zu können
addiert bzw. subtrahiert werden kann
42
Sachrechnen (In der Steinzeit)
52 – 56
M:
P:
Sachsituationen in Zeichnungen, Tabellen und/oder
D:
Informationen aus Tabellen entnehmen
Rechnungen übertragen
G:
Sachaufgaben mit Längen- und Gewichtsan-gaben lösen
Für sich entdecken, welche Lösungsstrategie die
D:
Informationen aus einem Sachtext für Aufgaben nutzen
sinnvollste ist
Z:
Eigene Lösungswege finden und passende Antworten
notieren
Kommentar/
Individueller Schwerpunkt
Arbeitsplan für Schuljahr: XX/XX
Zeitliche
Planung
Lerneinheit
52
Unterrichtsreihe/Thema
Vergrößern und Verkleinern
Zahlen
und
Rechnen
Teil A
Zahlen
und
Rechnen
Teil B
Größen
und
Sachrechnen
Geometrie
Prozessbezogene Kompetenzen
K: Kommunizieren, A: Argumentieren,
D: Darstellen, M: Modellieren, P: Problemlösen
34 – 37
M:
Inhaltsbezogene Kompetenzen
Z: Zahlen und Operationen, R: Raum und Form,
G: Größen und Messen, D: Daten, Häufigkeit und
Wahrscheinlichkeit, M: Muster und Strukturen
Informationen aus maßstäblich vergrößerten bzw.
R:
Zeichnungen anfertigen
verkleinerten Bild entnehmen und auf die Originalgröße
R:
Ebene Figuren verkleinert und vergrößert in Gitternetzen
schließen
P:
Verkleinerungen und Vergrößerungen mit Hilfe des
abbilden
R:
Maßstabs erkennen
53
Geobrett
38 – 40
P:
Kenntnisse zur Vergrößerung/Verkleinerung anwenden
P/A:
Vergrößerung und Verkleinerung berechnen
R:
Figuren in Maßquadrate einteilen; Kenntnisse über
Zerlegung von Quadraten in rechtwinklige Dreiecke
In zeichnerisch dargestellten Figuren durch Maßquadrate
den Flächeninhalt bestimmen
R:
anwenden und die Vorgehensweise erklären;
Kenntnisse über Symmetrie anwenden
Maße im Bild und im Original bei maßstäblicher
Figuren nachspannen und diese maßstäblich
vergrößern/verkleinern
R:
Auf einem Geobrett Figuren spiegeln
Kommentar/
Individueller Schwerpunkt