Allgemeines - etech – HAW Hamburg

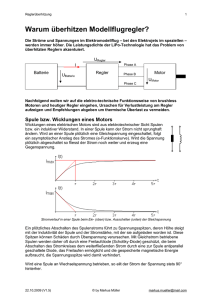
HAW Hamburg
Department Informations- und Elektrotechnik
Eingegangen am:
Labor für Automatisierungstechnik
Studiengruppe: _____________
Protokollführer/in:
__________________________
Übungstag: ________________
Weitere Übungsteilnehmer:
__________________________
Professor: _________________
__________________________
__________________________
Praktikum Grundlagen der Regelungstechnik
Allgemeines
Ziele
Die Teilnehmer sollen an Hand eines praxisnahen Beispiels die typischen Elemente eines Regelkreises
kennen lernen. Es werden unterschiedliche Dimensionierungsverfahren für Regler erprobt. Besonders
sollen das Führungs- und Störverhalten sowie statische und dynamische Kenngrößen untersucht werden.
Durchführung des Praktikums
Das Praktikum hat den Charakter eines Projekts. In vier Terminen soll das Ziel – Aufbau und Erprobung
eines Regelkreises – schrittweise erreicht
werden. Dabei soll an den einzelnen
Mechanischer Aufbau
Übungstagen in der Regel eins der
Drosselklappe
0100
1 75
folgenden Kapitel bearbeitet werden. Zu
jedem Termin wird von allen Teilnehmern eine Vorbereitung verlangt,
Ventilator
Heizung
PT-100
Differenzüber die die Teilnehmer in einem GeMeßsonde
drucksensor
spräch Auskunft geben können. Die
Vorbereitung ist notwendig, um die
Arbeitsschritte am Versuchstag sinnvoll
durchführen zu können. Über jeden
Arbeitstag ist ein Protokoll anzufertigen.
0 1
Meß-
blende
Versuchsaufbau
P
I
I
Im Labor für Automatisierungstechnik
steht für jede Praktikumsgruppe ein
Modell zur Temperaturregelung zur Verfügung (siehe nebenstehendes Bild). In
einem Rohr strömt Luft an einem
Heizelement entlang und wird dabei
Ventilator
Heizung
T
F
manuell
manuell
erwärmt. Über einen elektrischen Lüfter
intern
intern
Meßausgang
Meßausgang
kann die Strömungsgeschwindigkeit
Temperatur
Durchfluß
4...20mA
4...20mA
beeinflusst werden. Ziel kann es z.B. sein,
(Zweileitertechnik) (Zweileitertechnik)
einen
bestimmten
Volumenstrom
Ventilator
Heizung
erwärmter Luft oder Luft mit konstanter
extern
extern
Stellglied
4...20mA
4...20mA
Temperatur
unabhängig
von
der
Strömungsgeschwindigkeit
und
der
Umgebungstemperatur zu erzeugen.
Zur Regelung wird ein Industrieregler eingesetzt. Für die komfortable Bedienung des Reglers und für
begleitende Simulationen wird ein PC benutzt. Zur Messung von Temperatur und Volumenstrom sind
am Modell Messwertgeber mit Wandlern vorhanden, die den Messgrößen proportionale elektrische
Signale erzeugen.
-1-
V2.3.3 04.03.’11
Aufgabe 1: Die Temperatur-Regelstrecke
Allgemeines
Zur gezielten Auswahl eines geeigneten Reglertyps und zur Parametrierung des Reglers ist es
notwendig, die Daten der Regelstrecke zu kennen, um daraus ein ausreichend genaues mathematisches
Modell der Strecke zu bilden. Informationen über die Strecke liefern im Allgemeinen physikalische
Überlegungen, Gerätebeschreibungen und Messungen an der Anlage.
In diesem Praktikum soll die Strecke zur Erzeugung eines Luftstroms mit vorwählbarer Temperatur
benutzt werden. Zur Erwärmung wird das im Rohr eingebaute Heizelement benutzt, das über einen
Verstärker im Stellgliedmodul angesteuert wird. In der Schalterstellung „INT“ wird die Heizleistung
über ein Potentiometer zwischen 0 und 100% von Hand vorgegeben, während in der Stellung „EXT“ ein
Wert über Buchsen von außen eingespeist wird. Wie in der Verfahrenstechnik üblich, wird mit StromNormsignalen mit aktivem Nullpunkt gearbeitet. 4mA entsprechen 0% und 20mA 100%.
Vor der Austrittsöffnung wird die Temperatur mit einem Widerstandsthermometer Pt100 gemessen, das
die Änderung des elektrischen Widerstands von Platin mit der Temperatur zur Messung ausnutzt. In der
industriellen Messtechnik sind Widerstandsthermometer weit verbreitet. In der Versuchseinrichtung ist
ein Pt100 in Industrieausführung mit Linearisierung eingebaut. Über Buchsen an der Frontplatte des
Stellgliedmoduls kann der Messwert als Strom-Normsignal abgenommen werden.
Physikalische Grundlagen
Stationäres Verhalten
Im stationären Zustand wird die elektrische Leistung Pel , die dem System über die Heizung zugeführt
wird, vollständig in thermische Leistung Pth umgesetzt. Wird ein Luftvolumen V um die Temperatur 
erwärmt, so ist dem Volumen die Energie Wth zugeführt worden, mit
Wth  c L LV .
(1)
Pth erhält man durch Differenziation nach der Zeit:
dWth
dV
Pth 
 c L L
  c L LV  Pel ,
(2)
dt
dt
Wsec
mit c L  1,01
...spezifische Wärmekapazität von Luft
gK
kg
und  L  1,293 3 ... Dichte von Luft.
m
dx
Strömt die Luft mit der Geschwindigkeit v 
durch das Rohr mit dem Querschnitt A , so gilt für den
dt
Volumenstrom V  vA . Die Strömungsgeschwindigkeit v wird vom Ventilator geliefert. Für die
Austrittstemperatur gilt also:

1
1
Pth ,
c L L A v
(3)
 ist hierbei die Temperaturerhöhung gegenüber der Raumtemperatur.
Dynamisches Verhalten
Bevor die zugeführte elektrische Leistung vollständig als thermische Leistung abgegeben wird muss sich
zunächst das Heizelement mit seiner Ummantelung erwärmen. Außerdem muss die erwärmte Luft den
Weg vom Heizelement zur Temperatur-Messstelle zurücklegen. Für das Heizelement kann man sich
vereinfacht vorstellen, dass es aus einem homogenen Körper mit der Wärmekapazität C H und der
Temperatur  H an seiner Oberfläche besteht. Die im Heizelement gespeicherte Energie ist:
- WH  C H  H   Pel  Pth dt .
(4)
-2-
V2.3.3 04.03.’11
Differenziation nach der Zeit ergibt:
d H
 Pel  Pth .
dt
Mit (3) kann Pth eliminiert werden:
(5)
CH
d H
(6)
 Pel .
dt
Wird die elektrische Leistung Pel als Eingangsgröße und die Temperatur  H als Ausgangsgröße
c L L Av H  C H
betrachtet und die Strömungsgeschwindigkeit als konstant angenommen, erhält man die folgende lineare
Differenzialgleichung 1. Ordnung:
 H t  
C H d H t 
1

Pel t 
c L L Av dt
c L L Av
(7)
mit der zugehörigen Transformation in den Bildbereich der Laplace-Transformation:
CH
1
s H s  
Pel s .
c L L Av
c L L Av
 H s  
(8)
Führt man die Zeitkonstante
CH
c L L Av
TS 
(9)
und den Proportionalbeiwert
KS 
1
(10)
c L  L Av
ein, kann man die Übertragungsfunktion GH s  des Heizelements schreiben als:
G H s  
 H s 
Pel s 
 KS
1
.
1  TS s
(11)
Vernachlässigt man die Abkühlung des Luftstroms während des Transports vom Heizelement zur
Messstelle im Abstand l , werden Temperaturänderungen an der Oberfläche des Heizelements am Messort um die Transportzeit Tt verspätet wirksam. Dieses Verhalten kann als Totzeitglied im LaplaceBereich berücksichtigt werden:
Gt s  
T s
 s 
e t
H s 
(12)
mit
Tt 
l
v
(13)
Die Übertragungsfunktion GS s  der Regelstrecke für konstanten Volumenstrom lautet mit dieser
Modellvorstellung also:
 s 
T
s
e t
GS s  
 KS
.
Pel s 
1  TS s
(14)
Vorbereitung
In vielen Prozessen ist es möglich, einen so genannten Arbeitspunkt anzugeben. Der Arbeitspunkt stellt
den Satz von physikalischen Größen dar, der den typischen Betrieb der Anlage kennzeichnet. Besonders
sinnvoll ist die Arbeitspunktdefinition dann, wenn eine Regelung dafür sorgt, dass keine großen
Abweichungen von diesem Betriebspunkt auftreten. Für kleine Schwankungen um den Arbeitspunkt kann
eine lineare Übertragungsfunktion in solchen Fällen das Verhalten der Anlage oft ausreichend genau
beschreiben, auch wenn im Großen nichtlineare Verhältnisse vorliegen.
-3-
V2.3.3 04.03.’11
Machen Sie folgende Annahmen für ein mögliches Modell der Regelstrecke am Arbeitspunkt
(Strömungsgeschwindigkeit v  v L ):
K S  0,3
K
, TS  5 sec , Tt  1sec .
W
Die tatsächlichen Anlagenparameter werden am Versuchstag durch Messungen ermittelt. Sie weichen
deutlich von den obigen Modellwerten ab.

Berechnen und skizzieren Sie die Temperaturverläufe für
a) Pel t   10W   t  ,
b) Pel t   20W   t  ,
c) Pel t   30W   t  .

Berechnen und skizzieren Sie die Temperaturverläufe für Pel t   10W   t  unter der Annahme der
Strömungsgeschwindigkeit:
a) v  v L
vL
2
c) v  2  v L
b) v 

Berechnen und zeichnen Sie den Temperaturverlauf  t  für Pel t   50Wsec   t 


(Impulsantwort) unter der Annahme der Strömungsgeschwindigkeit v L .
Simulieren Sie die Zeitverläufe mit Matlab/Simulink.
Kommentieren Sie, inwieweit Sie erwarten können, dass Sie die vorausberechneten Zeitverläufe an
der Anlage nachmessen können.
Messungen
Im Arbeitspunkt gilt für die Heizungsansteuerung u yP  u yP 0  5V . Das entspricht einer Heizleistung
P0 von ca. 30 W. Die Lüfteransteuerung u yL  u yL 0  5V entspricht einer Luftgeschwindigkeit v0 von ca.
0,56 m/sec. (Die im Labor vorhandenen Regelstrecken sind in ihren Werten P0 und v0 leicht
unterschiedlich). Die Zuluftklappe soll geöffnet sein und die Heizwicklung in Stellung 1 bzw. P2
betrieben werden.
 Messen Sie mit einem elektronischen Temperaturfühler die Temperatur des Luftstroms am
Arbeitspunkt in °C und notieren Sie die zugehörigen Werte der Messwertgeber ( u x 0 , u xF 0 ),
nachdem sich der stationäre Zustand eingestellt hat. Wenn im Folgenden nicht anders angegeben ist,
sollen immer die Werte am Arbeitspunkt (Index 0) eingestellt bleiben.
 Wiederholen Sie die Messungen für 40%, 50% und 60% Heizleistung indem Sie für jede Heizleistung
die Lüfterspannung auf 60%, 50% und 40% variieren.
Bei den nachfolgenden Oszillografen ist auf eine hohe Auflösung zu achten (größtmögliche
Darstellung der Kurven). Um den kleinstmöglichen Messbereich am Oszilloskop wählen zu
können, ist der Offset des aufzuzeichnenden Signales, mit einer in Serie geschalteten
externen Spannungsquelle zu kompensieren.


Zeichnen Sie die Sprungantworten der Temperatur für Eingangssprünge der Heizleistung von 40%
auf 60% und von 60% auf 40% auf.
Zeichnen Sie die Sprungantworten der Temperatur für Eingangssprünge der Lüfterspannung von
40% auf 60% und von 60% auf 40% auf.
Auswertung
Stationäres Verhalten
Beziehen Sie sich für die folgenden Aufgaben auf Gl. (3). Gehen Sie davon aus, dass die Heizleistung Pel
proportional zur Heizungsansteuerung u yP und die Strömungsgeschwindigkeit der Luft v proportional
zur Lüfteransteuerung u yL ist.
-4-
V2.3.3 04.03.’11
Unter Verwendung der gemessenen Werte:
 Zeichnen Sie das Kennlinienfeld u x  f u yP mit u yL  4V, 5V, 6V als Parameter.
 Zeichnen Sie das Kennlinienfeld u x  f u yL mit u yP  4V, 5V, 6V als Parameter.
 Markieren Sie jeweils den Arbeitspunkt.
 
 
Für den Betrieb der Regelstrecke sind im Arbeitspunkt neben der Regelstreckenverstärkung
KS 

 u x
 Pel
die Ansteuerverstärkung Ku 
und die Messverstärkung K M 
wichtig.
 Pel

 u yP
Es gilt K ges 

 ux
 Ku  K S  K M .
 u yP
Bestimmen Sie aus den Messungen bzw. aus den gegebenen Daten die oben genannte
Verstärkung Kges um den Arbeitspunkt.
Dynamisches Verhalten
Für die Regelstrecke soll auf Grund der vorherigen Betrachtungen (Gl. (14)) ein Modell aus P-T1-Glied
mit Totzeit benutzt werden. Dazu werden aus der Sprungantwort aus u x  f t  (Sprung der Heizleistung) mit einem grafischen Näherungsverfahren die Zeitkonstante TS und die Totzeit Tt ermittelt.
Der Fehler ist gering, wenn TS = T g = Ausgleichszeit und Tt = Tu = Verzugszeit gesetzt werden.

Bestimmen Sie aus den Sprungantworten u x  f t  (Sprung der Heizleistung) die
Streckenparameter K ges , TS und Tt gem. Gl. (14).
u x
Wendetangente
u xmax
Wendepunkt
u x
min
0
Tu
t
Tg
-5-
V2.3.3 04.03.’11
Aufgabe 2: Der Industrieregler
Allgemeines
Zur Regelung von Prozessen der Verfahrenstechnik werden Industrieregler eingesetzt. Typische
Regelgrößen sind hier Drücke, Temperaturen, pH-Werte, Volumen- oder Massenströme, Füllstände,
Ventilstellungen. Der Regler wird mit dem Prozess über standardisierte analoge (0/4…20mA, 0…10V)
oder digitale Schnittstellen (z.B. Profibus) verbunden. Intern verfügt ein Industrieregler über einen
Mikroprozessor mit D/A- und A/D-Umsetzer. Außer dem digitalen Regelalgorithmus bearbeitet der
Prozessor noch die Bedien- und Anzeigeelemente auf der Frontplatte sowie ggf. Schnittstellen zu Leitsystemen. Komplexere Regler besitzen zusätzliche Funktionen wie Mehrreglerstrukturen und Selbstoptimierung.
-6-
V2.3.3 04.03.’11
Der Regler arbeitet quasistetig. Das heißt, obwohl der Regler intern digital (zeit- und wertdiskret)
arbeitet, kann man ihn wie einen analogen (zeitkontinuierlichen und stetigen) Regler behandeln. Das wird
durch die automatische Wahl einer ausreichend kurzen Abtastzeit und die hohe Auflösung der D/A- und
A/D-Umsetzer sichergestellt.
Der PID-T1-Regelalgorithmus lautet:
GR s  
y s 
 Kp
es 
1
1
 Tv s
Tn s
1  Ts
(15)
Der hier verwendete Industrieregler arbeitet nach einer PI(D-T1)-Übertragungsfunktion:
Tv' s 
ys 
1
' 


G s  
 K P 1  ' 
' 
es 
T
s
1

T
s
n


'
R
(16)
Einstellbar sind der Proportionalbeiwert K P' , die Nachstellzeit Tn' und die Vorhaltezeit Tv' . Die
Verzögerung T ' stellt sich intern auf T '  Tv' / 3 ein. Durch die Einstellungen auf Tn'  9999 bzw.
Tv'  0 können wahlweise der I-Anteil oder der D-Anteil außer Funktion gesetzt werden, so dass auch P-,
PI- oder PD- T1-Verhalten möglich ist.
Vorbereitung
 Berechnen Sie allgemein K P' , Tn' , Tv' , T ' als Funktionen von K P , Tn , Tv , T durch
Koeffizientenvergleich der Übertragungsfunktionen (15) und (16).
 Berechnen Sie K P' , Tn' , Tv' , T ' für K P  2 , Tn  9 sec , Tv  1,5 sec , T  Tv / 3 .
Aus Gl. (15) ergibt sich durch Transformation in den Zeitbereich:
yt   T

dyt 
1
det 
 K p et    et dt  Tv

dt
Tn
dt 

(17)
 Leiten Sie die Gleichung (17) her.
Der PID-T1-Regler hat die Sprungantwort:

T
T
t T
y t   K p 1 

   1  v
T
 Tn Tn  Tn
 t T 
e 


(18)

Es sei wieder KP = 2, Tn = 9 sec, TV = 1,5 sec, T = TV /3. Berechnen Sie die ersten 11 Werte der
Sprungantwort im Abstand von 1 sec und tragen Sie diese in eine Tabelle ein.
 Zeichnen Sie eine Skizze der Sprungantwort für 0 ≤ t ≤ 10sec.
 Leiten Sie für den Fall TV = 0 (PI-Glied) die Sprungantwort aus der Übertragungsfunktion (15) her
und vergleichen Sie Ihr Ergebnis mit (18).
 Berechnen Sie für 0 ≤ t ≤ 4sec die ersten fünf Werte der Sprungantwort des PI-Reglers.
Um eine Differenzialgleichung in eine Differenzengleichung umzuwandeln, kann man die
Differenzialquotienten
Mit t   und y ( t )
dy t 
det 
y t 
et 
und
durch die Differenzenquotienten
und
ersetzen.
dt
t
t
dt
 y (t  k )  y (t ( k 1) )  y k  y k 1 (entsprechendes gilt für et  ) wird aus der Dgl.
des Reglers (17) die Berechnungsvorschrift der Reglerausgangsgröße y k zum aktuellen Abtastzeitpunkt
(digitaler PID-T1-Algorithmus). Für den Fall TV = 0 wird daraus ein digitaler PI-Algorithmus:
 

y k  y k 1  K p ek 1 
  Tn




  ek 1 


(19)
Leiten Sie (19) her.
Berechnen Sie für (19) die ersten fünf Werte der Sprungantwort (KP = 2, Tn = 9 sec,   1sec ).
Vergleichen Sie mit der Sprungantwort des PI-Reglers.
-7-
V2.3.3 04.03.’11
h
h
Messungen
 Lassen Sie sich in die Bedienung des Industriereglers einweisen.
 Parametrieren Sie folgende Regler und nehmen Sie jeweils die Sprungantworten auf.
 P-Regler
: Kp=2
PI-Regler
P(D-T1)-Regler
: K p = 2,
: K p = 2,
Tn = 9 sec
Tv = 9 sec, T = ... sec
PI(D-T1)-Regler : K p = 2, Tn = 9 sec, Tv =1,5 sec

Parametrieren Sie den Regler als P-Regler mit KP = 2. Speisen Sie den Eingang mit einem
Sinusgenerator. Erhöhen Sie die Frequenz am Generator von 0 Hz ausgehend so weit, bis Sie deutlich
die Abtastschritte im Ausgangssignal erkennen können. Zeichnen Sie das Ausgangssignal auf und ermitteln Sie, mit welcher Abtastzeit  der Regler intern arbeitet.

Untersuchen Sie mit Matlab/Simulink1 die Unterschiede zwischen den Übertragungsfunktionen:
o Theoretische Übertragungsfunktion PID-T1 (Gl.15) mit den Parametern:
K P = 2, Tn = 9 sec, Tv =1,5 sec, T  Tv / 3
o Reale (Bürkert) Übertragungsfunktion PI(D-T1) (Gl.16) mit den Parametern:
K P' = K P , Tn' = Tn , Tv' = Tv , T '  T
o Reale (Bürkert) Übertragungsfunktion PI(D-T1) (Gl.16) mit den aus Koeffizientenvergleich
ermittelten Parametern:

T
K p'  K p 1 
 Tn


TT
 , Tn'  Tn  T , Tv'  n v  T , T '  T
Tn  T

Zeichnen Sie die Sprungantworten in einen gemeinsamen Graphen.
Hinweise zu Matlab/Simulink
Die Simulationsparameter von Matlab/Simulink sind wie folgt einzustellen:
Klicken Sie auf  ‚Simulation’  ‚Configuration Parameters… Ctrl+E’
es erscheint das Fenster:
Configuration Parameters:’model name’/Configuration
Machen Sie bei den folgenden Unterpunkten die Einträge:
Solver options
Type: Fixed-step,
Solver: ode2 (Heun)
Fixed-step size (fundamental sample time): …
 diese ‚sample time’ sollte kleiner 100 ms sein also < 0.1 !
1
Auswertung
 Entnehmen Sie aus dem Zeitverlauf der Ausgangsgröße des PI-Reglers die Reglerparameter K p und
Tn .

Entnehmen Sie aus dem Zeitverlauf der Ausgangsgröße des P(D-T1)-Reglers die Reglerparameter
K p , Tv und T .
-8-
V2.3.3 04.03.’11
Aufgabe 3: Die Temperaturregelung
Allgemeines
Die Austrittstemperatur der Luft soll geregelt werden. Der Industrieregler wird als Temperaturregler
eingesetzt, wobei die Heizleistung die Stellgröße ist. Um den Regler einstellen zu können, müssen die
Parameter der Strecke bekannt sein. Meistens wird mit einem linearen Modell der Strecke gearbeitet, das
zumindest um einen Arbeitspunkt herum näherungsweise gültig ist. Dazu sind unter Aufgabe 1
Messungen an der Regelstrecke gemacht worden.
Vorbereitung
Gemäß (14) wird erwartet, dass die Regelstrecke das Verhalten eines P-T1-Gliedes mit Totzeit hat. Die
Sprungantworten aus Aufgabe 1 bestätigen das angenähert. Mit einem grafischen Verfahren wurden aus
der realen Sprungantwort die Parameter eines P-T1-Tt-Modells ermittelt.
Um den Regler mit einem einfachen Verfahren auszulegen, kann durch eine weitere Näherung das
Totzeitglied durch ein P-T1-Glied ersetzt werden, wenn gilt Tt  TS :
T s
e t 
1
.
1  Tt s
(20)
Für die Übertragungsfunktion der Strecke gilt somit
GS s  


u x s 
1
1
.
 K ges
u yP s 
1  Tt s 1  TS s
(21)
Leiten Sie (20) her, indem Sie die Exponentialfunktion in eine Potenzreihe entwickeln, die Sie nach
dem linearen Glied abbrechen.
Zur Regelung soll ein PI-Regler eingesetzt werden,
GR s   K p
1  Tn s
.
Tn s
(22)
Stellen Sie die Führungsübertragungsfunktion Gw s  des Temperatur-Regelkreises auf.

Vereinfachen Sie Gw s  , indem Sie Tn  TS setzen.

Bestimmen Sie die Reglerverstärkung K p so, dass der Dämpfungsgrad  

Simulieren Sie eine Führungssprungantwort des Kreises mit der durchgeführten Dimensionierung.
Benutzen Sie für die Strecke das P-T2-Modell (21).
Simulieren Sie eine Führungssprungantwort des Kreises mit derselben Dimensionierung. Benutzen
Sie für die Strecke das P-T1-Tt-Modell.
Messen Sie in den simulierten Sprungantworten jeweils die Amplitude des ersten Überschwingers in
Prozent.
Simulieren Sie eine Störsprungantwort des Regelkreises.



1
2
wird.
Messungen
Bei den nachfolgenden Oszillografen ist auf eine hohe Auflösung zu achten (größtmögliche
Darstellung der Kurven). Um den kleinstmöglichen Messbereich am Oszilloskop wählen zu
können, ist der Offset des aufzuzeichnenden Signales, mit einer in Serie geschalteten
externen Spannungsquelle zu kompensieren.

Berechnen Sie u x und u yP für  soll  46C und nehmen Sie die Regelstrecke (offener Regelkreis)
mit diesen Werten in Betrieb. Lüfteransteuerung u yL  5V einstellen. Schalten Sie eine Störung zu,


indem Sie über den Schalter an der Strecke die Heizwicklung umschalten (Schalterstellung 1  0
bzw. P2  P1). Zeichnen Sie die Störsprungantwort auf.
Verbinden Sie den Regler mit der Strecke (geschlossener Regelkreis) und konfigurieren Sie den
Regler als Regler mit externem Sollwert.
Stellen Sie die von Ihnen berechneten Reglerparameter ein. Stellen Sie als Führungsgröße einen
Temperatursollwert von  soll 46C ein. Bringen Sie den Regler in die Betriebsart AUTOMATIK.
Beobachten Sie, ob sich die Temperatur auf den Sollwert einstellt.
-9-
V2.3.3 04.03.’11



Schalten Sie eine Störung zu, indem Sie über den Schalter an der Strecke die Heizwicklung
umschalten (Schalterstellung 1  0 bzw. P2  P1). Nehmen Sie die Störsprungantwort auf.
Zeichnen Sie dabei die Regelgröße u x (Temperaturistwert) und die Stellgröße u yP (Reglerausgang)
auf.
Nehmen Sie eine Führungssprungantwort auf. Der Führungssprung ist dabei vom Arbeitspunkt
ausgehend in der Höhe zu setzen, bei dem der Reglerausgang nicht in die Begrenzung geht. Zeichnen
Sie dabei die Regelgröße u x (Temperaturistwert) und die Stellgröße u yP (Reglerausgang) auf.
Lassen Sie sich die Funktion TUNE des Reglers erklären. Wenden Sie gemäß der
Bedienungsanleitung die Funktion TUNE an, um die Reglerparameter vom Regler selbst ermitteln
zu lassen. Nach den getätigten Voreinstellungen am Regler wird die TUNE-Funktion mit einem
Führungssprung von W  10% gestartet. Notieren Sie anschließend die neuen Reglerparameter
und nehmen Sie wie bei den beiden vorigen Punkten eine Führungs- und Störsprungantwort mit
dieser Reglereinstellung auf.
Auswertung
 Überprüfen Sie theoretisch die stationäre Genauigkeit des Regelkreises bei Führungs- und
Störanregung mit Hilfe des Endwertsatzes der Laplace-Transformation. Kommt es zu einer
bleibenden Regeldifferenz?
 Lässt sich diese Vorhersage durch die Messungen belegen?
 Messen Sie in den Führungssprungantworten die Amplitude des ersten Überschwingers in Prozent.
 Vergleichen Sie die Werte für die ersten Überschwinger und kommentieren Sie die Ergebnisse.
- 10 -
V2.3.3 04.03.’11
Aufgabe 4: Die Volumenstromregelung
Allgemeines
 Die Messung des Volumenstroms geschieht über die Erfassung der Druckdifferenz, die die
strömende Luft an einer im Rohr befindlichen Messblende hervorruft. Als Stellgröße wird
die Lüfterspannung verwendet, die über die Veränderung der Lüfterdrehfrequenz den
Volumenstrom beeinflusst.
 Zur Bestimmung der Reglerparameter könnte man sich wie bei der Regelgröße Temperatur
auch hier bemühen, die Streckenübertragungsfunktion (näherungsweise) zu bestimmen. Als
Variante soll hier jedoch die Reglereinstellung nach den Einstellregeln von Ziegler/Nichols
vorgenommen werden. Dabei wird der Regelkreis an seine Stabilitätsgrenze gebracht, um
aus den dort gewonnenen Daten die optimale Betriebseinstellung zu finden. Nach einem
abgewandelten Verfahren kann der Regler über die Funktion ‚TUNE‘ auch selbsttätig seine
Betriebseinstellung finden. Diese Funktion soll ebenfalls beobachtet werden.
Vorbereitung
 Informieren Sie sich über die Einstellregeln nach Ziegler/Nichols. Zur Anwendung kommt
die Methode für geschlossene Regelkreise.
3



 1 
Nehmen Sie an, eine Regelstrecke habe folgende Übertragungsfunktion: GS s   
 .
 1  Ts 
Zur Regelung werde ein P-Regler mit GR s   K P eingesetzt.
Berechnen Sie die Führungsübertragungsfunktion Gw s  .

Simulieren Sie den angegebenen Regelkreis in Matlab/Simulink mit T  1sec und K P  2 .
Zeichnen Sie eine Führungs- und eine Störsprungantwort auf.
 Berechnen Sie die Polstellen der Übertragungsfunktion des geschlossenen Kreises.
 Ermitteln Sie experimentell in der Simulation die Stabilitätsgrenze, indem Sie die
Reglerverstärkung verändern. Notieren Sie die Reglereinstellung KPkrit und die Periodendauer
Tkrit der Schwingungen an der Stabilitätsgrenze.
Bei den hier für die Simulation angegebenen Streckenparametern handelt es sich um
Beispielwerte, die von den tatsächlichen Anlagenparametern abweichen !
Messungen
 Stellen Sie an der Strecke den Arbeitspunkt u yL  5V ein. Bestimmen Sie u xF 0 .
Verändern Sie die Lüfterspannung auf u yL  4V und u yL  6V und messen Sie die zugehörigen Volumenströme. Bestimmen Sie aus den gemessenen Werten die Verstärkung KSF der
Volumenstrom-Strecke am Arbeitspunkt.
Bei den folgenden Messungen sind die Kurvenverläufe mit den jeweils signifikanten Größen
(Regel- und Stellgröße) in einem Oszillografen darzustellen!
Auf eine hohe Auflösung der Oszillografen ist zu achten (größtmögliche Darstellung der
Kurven). Um den kleinstmöglichen Messbereich am Oszilloskop wählen zu können, ist der
Offset des aufzuzeichnenden Signales, mit einer in Serie geschalteten externen
Spannungsquelle zu kompensieren.




Stellen Sie wieder u yL  5V ein. Legen Sie den Hebel an der Zuluftöffnung um und
oszillografieren Sie den verminderten Volumenstrom uxFz.
Verbinden Sie den Industrieregler mit der Strecke zu einer Volumenstromregelung.
Konfigurieren Sie den Regler als P-Regler. Stellen Sie den Arbeitspunkt y 0  50% ein.
Stellen Sie die Reglerverstärkung so ein, dass Dauerschwingungen entstehen.
Oszillografieren Sie die Dauerschwingungen und notieren Sie die Reglereinstellung KPkrit
sowie die Periodendauer Tkrit der Schwingungen an der Stabilitätsgrenze.
- 11 -
V2.3.3 04.03.’11



Stellen Sie den Regler gemäß den Einstellregeln nach Ziegler-Nichols als P-Regler ein.
Schließen Sie den Hebel an der Zuluftöffnung und oszillografieren Sie den Einfluss dieser
Störung.
Stellen Sie den Regler nun als PI-Regler nach Ziegler-Nichols ein und wiederholen Sie die
Aufzeichnung.
Nehmen Sie mit Hilfe der TUNE-Funktion die Einstellung des Reglers vor und vergleichen
Sie das jetzige Verhalten mit der Einstellung nach Ziegler-Nichols anhand der zuvor
gemachten Oszillografen.
Auswertung
 Stellen Sie die Störübertragungsfunktion G Z  s  für das geregelte System mit P-Regler auf
und berechnen Sie den Endwert mit Hilfe des Endwertsatzes der Laplace-Transformation.
 Berechnen Sie den Endwert für das ungeregelte System (nur Regelstrecke !) mit Hilfe des
Endwertsatzes der Laplace-Transformation.
 Bilden Sie das Verhältnis bei Störanregung vom geregelten zum ungeregeltem System und
vergleichen Sie das Ergebnis mit den Werten aus den im Praktikum erstellten Oszillografen.
- 12 -
V2.3.3 04.03.’11