Chemische Verschiebung - Lage der Resonanzsignale

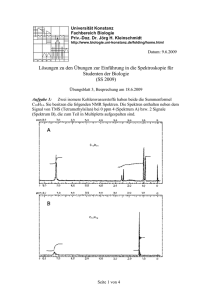
Sie benötigen zur Konstruktion des Spektrums mehrere Angaben, die Sie am besten
schrittweise aus der Struktur der Verbindung ableiten:
1. Wie viele Gruppen äquivalenter Protonen und damit Resonanzsignale
werden gefunden?
1. Wodurch wird die Zahl der von einer Verbindung zu erwartenden 1H-NMR-Signale
bestimmt?
2. Wann bezeichnet man H-Atome als äquivalent?
3. Wie können äquivalente H-Atome in einer gegebenen Verbindung gefunden werden?
4. Wie verhalten sich die H-Atome der Methyl- bzw. der Methylengruppen?
1. Die Zahl der Signale im 1H-NMR-Spektrum einer Verbindung ist gleich der Anzahl
der Gruppen äquivalenter H-Atome.
2. H-Atome sind dann äquivalent, wenn sie gleichartig gebunden sind, d.h., wenn die
Geometrie des Restmoleküls bezüglich der H-Atome identisch ist, wenn der
Bindungscharakter der benachbarten Bindungen identisch ist.
3. Um äquivalente H-Atome in einer Verbindung aufzufinden, kann entweder das
Restmolekül der Reihe nach von allen H-Atomen aus betrachtet und beobachtet
werden, wann übereinstimmende Umgebungsverhältnisse auftreten, oder nach
Symmetrieelementen des Moleküls gesucht werden, die verschiedene H-Atome
einander zuordnen.
4. In frei beweglichen Systemen ergeben die H-Atome von Methyl- oder
Methylengruppen jeweils ein gemeinsames Signal.
2. Welche Werte der chemischen Verschiebung erwarten Sie für die
Gruppen äquivalenter Protonen?
Chemische Verschiebung - Lage der Resonanzsignale
Um das NMR-Spektrum für eine vorgegebene Verbindung konstruieren zu können, muss man
die Anzahl der Resonanzsignale und natürlich ihre Lage im Spektrum, d. h. die Werte ihrer
chemischen Verschiebungen kennen. Auch für diese sind Voraussagen möglich:
Äquivalente Protonen in Molekülen ergeben auf Grund der gleichen Elektronenverteilung in
ihrer Umgebung gleiche chemische Verschiebungen. Haben nun zwei Protonen ähnliche
chemische Umgebungen, dann werden ihre Signale im Spektrum nage beieinander liegen. So
werden z. B. die Signale der Methylprotonen der beiden Gruppen -CH2-CH3 und >CH-CH3
ähnliche
chemische
Verschiebungen
zeigen).
Die Analyse vieler Spektren ergibt, dass das Signal der Methylprotonen in aliphatischen
Verbindungen in den meisten Fällen in dem Erwartungsbereich der chemischen Verschiebung
von  = 0,6 ... 1,9 ppm liegt. Dagegen führt die vollkommen andere Elektronenstruktur der
Carbonylgruppe -CHO auch zu einem anderen Erwartungsbereich der chemischen
Verschiebung von  = 9,l ... l0 ppm für das Proton der Aldehydgruppe.
Die chemische Verschiebung kann quantitativ angegeben werden:
1. als Frequenzdifferenz  zwischen dem Signal S einer Standardverbindung, meist
Tetramethylsilan (TMS) und dem betrachteten Signal Pr der Probe, d.h.
Pr = Abstand des Probesignals vom TMS-Signal.
Dazu
eine
Erläuterung:
Auf Grund der Proportionalitätsbeziehung zwischen der magnetischen Feldstärke und der
Frequenz des elektromagnetischen Wechselfeldes nach
 = (/2 ) · Hz
ist es üblich, die chemische Verschiebung nicht in Feldstärke-, sondern in den
Frequenzeinheiten Hertz (Hz) (engl. cps = cycles per second) anzugeben.
2. in der -Skala nach der Formel:
 = (Pr · 106) / 0 ppm
(1ppm = 1 · 106 (parts per million); 0 ist die Arbeitsfrequenz)
Auf diese Art und Weise wird die chemische Verschiebung unabhängig von der
Arbeitsfrequenz
0,
denn:
Die Frequenzdifferenz  allein ist abhängig von der Arbeitsfrequenz 0 und gestattet
deshalb keine Vergleiche der chemischen Verschiebungen bei verschiedenen
Arbeitsfrequenzen (z.B. bei 250 MHz und 400 MHz).
3. in alten Spektren in der -Skala (nur bei Protonenresonanz) nach der Formel
 = 10 - 
3. Welche relativen Intensitäten besitzen die Signale der Gruppen
äquivalenter Protonen?
1. Warum können über die chemischen Verschiebungen von Protonensignalen
Voraussagen gemacht werden?
2. In welchen Skalen wird die chemische Verschiebung gemessen?
3. Wie wird die Intensität der Resonanzsignale gemessen?
4. Warum können die Signalintensitäten ergänzende Aussagen über die Struktur von
Verbindungen liefern?
1. Befinden sich Protonen in ähnlichen chemischen Umgebungen, dann haben ihre
chemischen Verschiebungen auch ähnliche Werte. Es ist deshalb möglich, für
charakteristische Protonengruppierungen Erwartungsbereiche für die chemischen
Verschiebungen zu tabellieren.
2. Die chemische Verschiebung kann gemessen werden
a. als Frequenzdifferenz  zwischen dem Signal einer Standardverbindung
(meist Tetramethylsilan - TMS) und dem betrachteten Signal der Probe;
b. als frequenzunabhängige Größe in der -Skala nach der Formel:
 = ( · 106)/ 0 ppm
wobei 0 die Arbeitsfrequenz des Spektrometers ist.
3. Die Intensität wird als Fläche (meist automatische Integration und daraus resultierende
Integralkurve) unter dem Resonanzsignal gemessen.
4. Die Intensität ist proportional der Anzahl der äquivalenten Protonen, die das Signal
bewirken. Deshalb verhalten sich die relativen Intensitäten der Signale einer
Verbindung wie die Zahlen der die Signale bewirkenden Protonen.
4. Welche Aufspaltungsbilder treten für die Resonanzsignale auf Grund der
Spin-Spin-Kopplung auf? (Art der Multipletts und Intensitäten der
Multiplettlinien)
1. Wodurch kommt es zur Aufspaltung von Resonanzsignalen?
2. Wie nennt man diese Erscheinung?
3. Wie können Sie die Anzahl der Linien eines Multipletts, d.h. die Multiplizität eines
Signals bestimmen?
4. Können Sie etwas über die relativen Intensitäten der Einzellinien eines Multipletts
voraussagen?
1. Treten die Magnetfelder zweier H-Atomkerne miteinander in Wechselwirkung, so
werden deren Energieniveaus im äußeren Magnetfeld weiter aufgespalten. Dadurch
werden mehrere nahe beieinanderliegende Übergänge möglich.
2. Wegen dieser durch die Bindungselektronen vermittelten Wechselwirkung bezeichnet
man die Erscheinung als indirekte Spin-Spin-Koplung.
3. Koppeln allgemein n äquivalente H-Kerne X mit dem Proton A, ergibt sich für die
Multiplizität MA der Aufspaltung des Signals A die Formel:
MA = n X + 1
4. Die relativen Intensitäten der Einzellinien eines Multipletts verhalten sich wie folgt:
Multiplizität
2
3
4
5
Relative Intensitäten
1:1
1:2:1
1:3:3:1
1:4:6:4:1
Die Aufspaltung der Signale wird durch die indirekte Spin-Spin-Kopplung verursacht.
Diese Bezeichnung weist schon darauf hin, dass die durch die Kernspins verschiedener Atome
(hier werden nur Protonen berücksichtigt!) verursachten Magnetfelder miteinander in
Wechselwirkung treten. Diese Kopplung der Kernspins wird über die Bindungselektronen mit
ihren
Magnetfeldern
vermittelt.
Ein
Beispiel:
Die beiden H-Atome im Dichloracetaldehyd (Dichlorethanal)
Cl2CH - CHO
X
A
zeigen
indirekte
Spin-Spin-Kopplung:
Im äußeren Feld B0 spaltet das Energieniveau des Kerns A wegen der Einstellung des
Kernspins in Richtung bzw. gegen die Richtung des äußeren Feldes auf. Damit wird ein
Übergang zwischen den beiden Niveaus (= ein Resonanzsignal) möglich.
Da der Kernspin des Kerns X ebenfalls zwei Einstellungsmöglichkeiten zum äußeren Feld
(mIX = + ½ und mIX = - ½) hat, wird nun, vermittelt durch die Bindungselektronen, das
wirksame äußere Feld am Kern A zweifach modifiziert. Dadurch spaltet jedes Niveau des
Kerns A noch einmal um einen geringen Betrag auf, und statt des einen Übergangs
werden zwei Übergänge möglich (= Dublett). Ein benachbartes H-Atom erzeugt also ein
Dublett (nX = 1 daraus folgt MA = 2)
5. Welche Werte haben die Kopplungskonstanten der Spinmultipletts?
Ein Maß für die Stärke der Kopplung zwischen zwei Gruppen A und X äquivalenter Protonen
ist die Kopplungskonstante JAX:
JAX = Abstand benachbarter Einzellinien des Multipletts A in Hertz
Zusammengehörige Kopplungskonstanten (JAX und JXA) sind gleich groß!
Die Kopplungskonstante J ist im Gegensatz zur chemischen Verschiebung eines
Resonanzsignals
eine
frequenzbzw.
feldunabhängige
Größe.
Zum Beispiel für das Dublett der Methylprotonen in (CH3)3CH-O-CH(CH3)2 gilt:
JCH3,CH (bei 0 = 250 MHz) = 6,1 Hz
(bei 0 = 600 MHz) = 6,1 Hz
Da in der Spektrendarstellung bei höheren Arbeitsfrequenzen die Entfernung der Signale in
ppm unverändert bleibt, während die Multiplettlinien eines Signals näher zusammenrücken,
werden die Spektren mit hohem Kopplungsanteil übersichtlicher und damit leichter
auswertbar. Deshalb besteht der Trend, Spektren bei immer höheren Arbeitsfrequenzen
(derzeit bis 800 MHz) aufzunehmen.
Unter welchen Bedingungen erwarten Sie keine Kopplung zwischen Protonen einer
Verbindung?
1. bei größerer Entfernung der Protonen, z.B.
H-C-C-C-H
2. innerhalb Gruppen äquivalenter Protonen, z.B.
Spin-Spin-Kopplung mit benachbarten Protonen:
Befinden sich in der Nachbarschaft eines Protons A
1. n andere äquivalente Protonen X, dann führt die Kopplung zwischen A und X zu einer
Aufspaltung des Signals von A mit der Multiplizität
MA = nX + 1
2.
3. mehrere
verschiedene
Sätze
äquivalenter
Protonen
M,
X...
(z.B. CHnM- CHA=CHnX) mit jeweils nM, nX .... Protonen, dann koppeln sie
unabhängig voneinander mit dem Proton A. Die Aufspaltung des Resonanzsignals von
A berechnet sich dann nach
MA = (nM + 1) * (nX + 1) ...
Für die Verbindung
ClCH = CH - CH2Cl
lassen sich Zahl und
M
A
X
relative Intensitäten der Multiplettlinien des Signals von HA anschaulich unter Verwendung
der
Kopplungskonstanten
ableiten.
Für HA gilt:

A = 4,86 ppm; JAM = 13,1 Hz; JAX = 7,3 Hz.
Die Kopplung von HA mit HM ergibt ein Dublett (nM = 1; relative Intensitäten 1: 1). Durch die
davon unabhängige zusätzliche Kopplung mit HX werden nun beide Dublettlinien noch
einmal zu je einem Triplett (nX = 2; relative Intensitäten 1: 2: 1) aufgespalten. Insgesamt
erscheinen
also
sechs
Einzellinien
(MA
=
6).
1. Wann erwarten Sie indirekte Spin-Spin-Kopplung zwischen Protonengruppen?
2. Wie wird die Multiplizität der Aufspaltungen durch Spin-Spin-Kopplung für
a. eine benachbarte nichtäquivalente Protonengruppe,
b. mehrere benachbarte nichtäquivalente Protonengruppen berechnet?
3. Wie verhalten sich die Intensitäten der Einzellinien eines durch eine benachbarte
nichtäquivalente Protonengruppe verursachten Multipletts?
4. Wie ist die Kopplungskonstante definiert, und welche Bedeutung hat sie?
1. Zwischen Protonengruppen einer Verbindung treten indirekte Spin- Spin- Kopplungen
auf, wenn die Protonen der verschiedenen Gruppen
a. nicht äquivalent und
b. nicht zu weit voneinander entfernt sind (z. B. in -Systemen im allgemeinen
nicht weiter als drei - Bindungen).
2. Die Multiplizität der Aufspaltung des Signals einer Protonengruppe A durch
Kopplung
a. mit einer benachbarten anderen Protonengruppe X mit nX äquivalenten
Protonen berechnet sich nach
MA = n X + 1
b. mit mehreren verschiedenen benachbarten Protonengruppen M, X,... mit
jeweils nM, nX,... äquivalenten Protonen berechnet sich nach
MA = (nM + 1)* (nX+ 1)...
3. Die Intensitäten der Einzellinien eines durch eine benachbarte Protonengruppe
verursachten Multipletts verhalten sich wie die n-ten Binominalkoeffizienten
(Pascalsches Dreieck).
4. Die Kopplungskonstante JAX ist ein Maß für die Stärke der indirekten Spin-SpinKopplung zwischen den Protonen A und X. Sie ist definiert als:
JAX = Abstand benachbarter Einzellinien des Multipletts A, hervorgerufen durch die
Kopplung
mit
X,
in
Hertz.
Die Größe der Kopplungskonstanten ist unabhängig von der Arbeitsfrequenz.