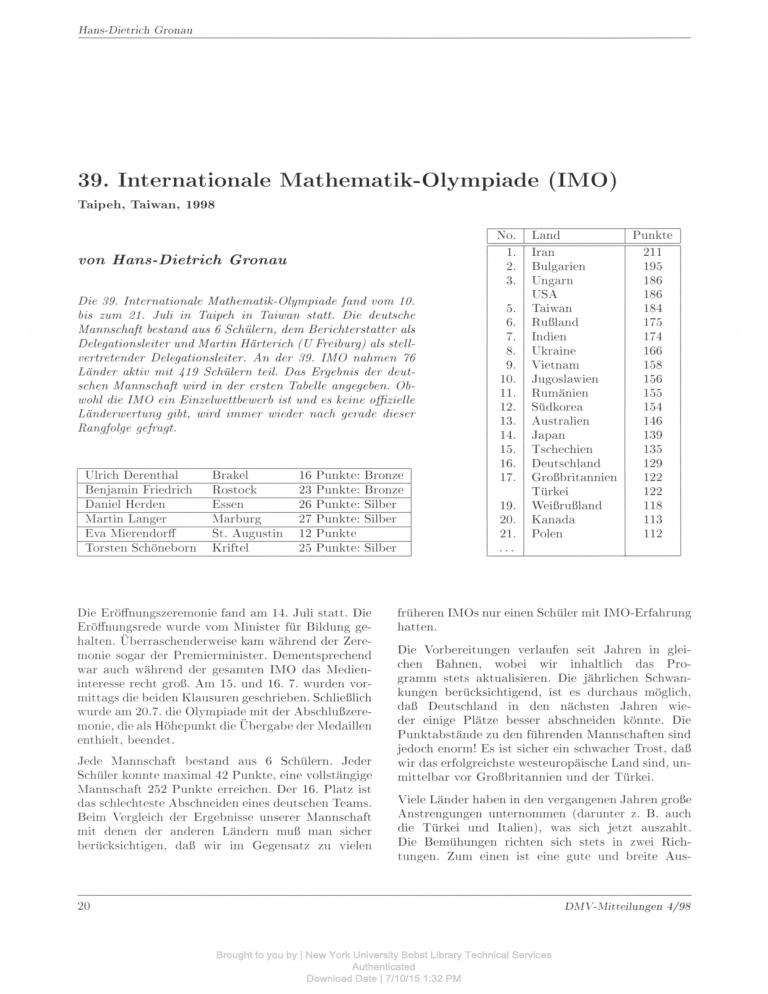
Hans-Dietrich Gronau 39. Internationale Mathematik-Olympiade (IMO) Taipeh, Taiwan, 1998 I No. 1. 2. 3. v on Hans-Dietrich Gronau Die 39. Internationale Mathematik-Olympiade f and vom 10. bis zum 21. Juli in Taipeh in Taiwan statt. Die deutsche Mannschaft bestand aus 6 S chülern, dem B erichterstatter als D elegationsleiter und Martin Härterich ( U Freiburg) als stellvertretender Delegationsleiter·. An deT 39. !MO nahmen 76 Länder aktiv mit 419 S chülern teil. Das Ergebnis der deutschen Mannschaft wiTd in deT eTsten Tabelle angegeben. Obwohl die !MO ein EinzelwettbeweTb ist und es keine offizielle LänderweTtung gibt, wiTd immeT wieder nach ger·ade dieser· Rangfolge gefmgt. Ulrich Derent hai Benj amin Friedrich Daniel Herden ".\1artin Langer Eva ".\Iierendorff Torsten Schöneborn Brakel Rosteck Essen l\Iarburg St. Augustin Kriftel 16 23 26 27 12 25 Punkte: Punkte: Punkte: Punkte: Punkte Punkte: Bronze Bronze Silber Silber Silber Die Eröffnungszeremonie fand am 14. Juli statt. Die Eröffnungsrede wurde vom Minister für Bildung gehalten. Überraschenderweise kam während der Zeremonie sogar der Premierminister. Dementsprechend war auch während der gesamten IMO das Medieninteresse recht groß. Am 15. und 16. 7. wurden vormittags die beiden Klausuren geschrieben. Schließlich wurde am 20.7. die Olympiade mit der Abschlußzeremonie, die als Höhepunkt die Übergabe der Medaillen enthielt, beendet. J ede Mann chaft besta nd aus 6 Schülern . J eder Schüler konnte maximal 42 Punkte, eine vollstä ngige Mannschaft 252 Punkte erreichen. Der 16. Platz ist das schlechteste Abschneiden eines deutschen Teams. Beim Vergleich der Ergebnisse unserer Mannschaft mit denen der anderen Ländern muß man sicher berücksichtigen, daß wir im Gegensatz zu vielen 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 19. 20. 21. Land Iran Bulgarien Ungarn SA Taiwan Rußland Indien Ukraine Vietnam Jugoslawien Rumänien Südkorea Australien J apan T schechien Deutschland Großbritannien Türkei Weißrußland Kanada Polen I Punkte I 211 195 186 186 184 175 174 166 158 156 155 154 146 139 135 129 122 122 118 113 112 . .. früheren IMOs nur einen Schüler mit Il\!0-Erfahrung ha tten. Die Vorbereitungen verlaufen seit Jahren in gleichen Bahnen, wobei wir inhaltlich das P rogramm stets aktualisieren. Die jährlichen Schwankungen berücksichtigend , ist es durchaus möglich, daß Deutschland in den nächsten J ahren wieder einige P lätze besser abschneiden könnte. Die Punktabst ände zu den führenden Mannschaften sind jedoch enorm! Es ist sicher ein schwacher Trost, daß wir das erfolgreichste westeuropäische Land sind, unmittelbar vor Großbritannien und der Türkei. Viele Länder haben in den vergangenen J ahren große Anstrengungen unternommen (darunter z. B. auch die Türkei und Italien), was sich jetzt auszahlt. Die Bemühungen richten sich stets in zwei Richtungen . Zum einen ist eine gute und breite Aus- 20 DMV-Mitteilungen 4/98 Brought to you by | New York University Bobst Library Technical Services Authenticated Download Date | 7/10/15 1:32 PM 39. In ternationale Mathem atik-Oly mpiade in Taipeh wahl , möglichst bereits durch motivierende Wettbewerbe in Sekundarstufe I, a ußerordentlich wicht ig. und zum anderen eine umfangreichere Vorbereitung der Ka ndidaten unerläßlich. Ersteres wäre in Deutschland leicht zu bewerkstelligen , da es bereits die :\Ia thematik-Olympiaden bundesweit gibt. Durch unterstützung und Förderung durch Bund oder Kultusministerkonferenz wäre sicher eine noch breitere Basis relati,· leicht erreichbar. Zur Zeit nehmen an der 2. Stufe mehr als 25000 Schülerinnen und Schüler teil. medaillisten und dem Nevanlinna-Preisträger des Mathematiker-Weltkongresses ICM 98 im August in Berlin alle eigene Erfahrungen mit mathematischen Wettbewerben hatten, 3 selbst !MO-Preisträger waren und ein Vierter sich 1980 für die Ii\IO qualifiziert hatte, in diesem J ahr jedoch letztlich keine 1:\1[0 stattfand. Für weitere Informationen über Ii\IOs und andere mathematische Schülerwettbewerbe sei auf die Homepage http://www.math.uni-rostock . de/MO des Mathematik-Olympiaden e.V. hingewiesen. Der :\ u t zen von ma thema tischen Schüler\\'ettbewerben für die Begeisterung für die i\Iathematik ist weltweit anerkannt. i\Ia nchmal wird die Meinung vertreten, daß Klausurwettbewerbe eher von der .. richtigen " _l[athematik ablenken. Interessant ist es in diesem Zusammenhang, daß von den 4 Fields- Adresse des Autors : Prof. Dr. Hans-Dietrich Gronau niversität Rostock, FB Mathematik 18055 Rostock Tel.: (0381) 4981539 [email protected] Aufgaben 1. Tag 2. Tag 1. In einem konvexen \ "iereck ABCD stehen die Diagonalen .-l.C und BD senkrecht aufeinander und die 4. Man bestimme alle Paare (a, b) positiver ganzer Zahlen , so daß a 2 b + a + b durch ab2 + b + 7 teilbar (Großbritannien) ist! gegenüberliegenden Seiten AB und DC sind nicht parallel. Die :\1ittelsenkrechten von AB und DC sehn iden sich im Punkt P innerhalb von ABC D. :\Ian beweise: .-l.BC D ist dann und nur dann ein Sehnenviereck. wenn die Dreiecke ABP und C DP gleichen Flächeninhalt haben. (Luxemburg) 2. In einem \Yettbewerb gibt es a Teilnehmer und b Preisrichter. wobei b 2 3 eine ungerade ganze Za hl ist. J eder Preisrichter beurteilt jeden Teilnehmer entweder mit " bestanden " oder mit "durchgefallen ". Für die Zahl k gelte: J e zwei Preisrichter stimmen in ihren urteilen bei höchstens k Teilnehmern überein. i\Ian beweise: k b- 1 >-a - 2b · 5. Es sei I der Inkreismittelpunkt des Dreiecks ABC. Die Berührungspunkte dieses Inkreises mit den Seiten B C, CA bzw. AB seien K , L bzw. JII. Die Gerade durch B parallel zu JII K schneidet die Geraden Ll\I bzw. LK in den Punkten R bzw. S . :\Ian beweise, daß 1: RIS ein spitzer Winkel ist! (Ukraine) 6. Ma n betrachte alle Funktionen f YOn der :\1enge N+ der positiven ganzen Zahlen in sich, die f (t 2 f (s)) = s(J(t )) 2 für alle s, t EIN+ erfüllen. Man bestimme den kleinstmöglichen Wert von ] (1998)! (Bulgarien) (Indien) 3. Für jede positive ganze Zahl n bezeichne d(n) die Anzahl der positiven Teiler von n (einschließlich 1 und n). :\Ian bestimme alle positiven ganzen Zahlen k . für die es ein n gibt, so daß gilt: d(n2) d(n) =k · (Weißrußland) Arbeitszeit: 4 ~ Stunden an jedem Tag. Bei jeder Aufgaben waren- 7 Punkte erreichbar. 21 DM\ ·-.1\Iitteilungen 4/98 Brought to you by | New York University Bobst Library Technical Services Authenticated Download Date | 7/10/15 1:32 PM











