¨Ubungen zur Theoretischen Elektrotechnik II
Werbung
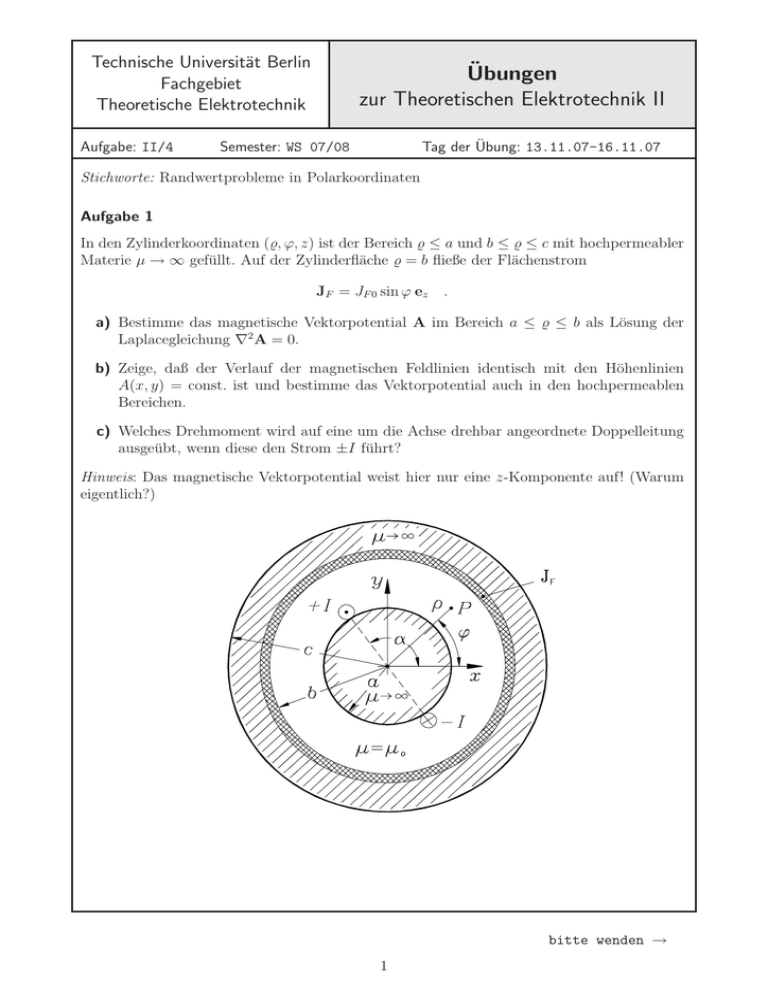
Technische Universität Berlin Fachgebiet Theoretische Elektrotechnik Aufgabe: II/4 Übungen zur Theoretischen Elektrotechnik II Semester: WS 07/08 Tag der Übung: 13.11.07-16.11.07 Stichworte: Randwertprobleme in Polarkoordinaten Aufgabe 1 In den Zylinderkoordinaten (̺, ϕ, z) ist der Bereich ̺ ≤ a und b ≤ ̺ ≤ c mit hochpermeabler Materie µ → ∞ gefüllt. Auf der Zylinderfläche ̺ = b fließe der Flächenstrom JF = JF 0 sin ϕ ez . a) Bestimme das magnetische Vektorpotential A im Bereich a ≤ ̺ ≤ b als Lösung der Laplacegleichung ∇2 A = 0. b) Zeige, daß der Verlauf der magnetischen Feldlinien identisch mit den Höhenlinien A(x, y) = const. ist und bestimme das Vektorpotential auch in den hochpermeablen Bereichen. c) Welches Drehmoment wird auf eine um die Achse drehbar angeordnete Doppelleitung ausgeübt, wenn diese den Strom ±I führt? Hinweis: Das magnetische Vektorpotential weist hier nur eine z-Komponente auf! (Warum eigentlich?) bitte wenden → 1 Hausaufgabe Gegeben sei ein sehr langer in x-Richtung homogen polarisierter Zylinder (Polarisation P = ex P0 ) vom Radius a. Berechne das elektrische Feld innerhalb des Zylinders. Hinweis: Bestimme zunächst die äquivalenten Polarisationsladungen auf der Zylinderoberfläche. 2











