Gemischte Übungen 2

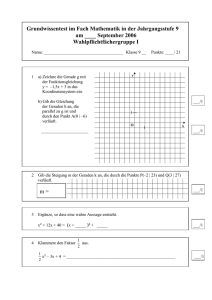
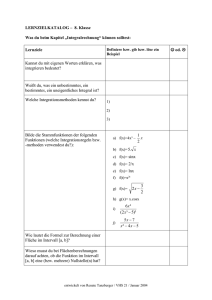
GEMISCHTE ÜBUNGEN 2
1) In Österreich fand am 25. April 2010 die zwölfte Wahl eines österreichischen Staatsoberhaupts durch das
Bundesvolk seit 1951statt. Bei der Wahl traten neben dem amtierenden Bundespräsidenten Heinz Fischer die
niederösterreichische Landesrätin Barbara Rosenkranz (FPÖ) und der Parteivorsitzende der CPÖ, Rudolf Gehring,
an. Dr. Heinz Fischer wurde mit 79,33 % der gültigen Stimmen klar im Amt bestätigt .
a) Wie groß war nach der Wahl die Wahrscheinlichkeit, dass sich unter 200 zufällig ausgewählten
Personen mindestens 170 Dr.-Heinz-Fischer-Wähler/innen befanden?
Berechne die Wahrscheinlichkeit durch Annäherung mit einer Normalverteilung.
b) Wie viele Personen mussten mindestens über ihr Wahlverhalten befragt werden, damit mit einer
Wahrscheinlichkeit von wenigstens 99 % mindestens ein/e Dr.-Heinz-Fischer-Wähler/in gefunden
wurde? (Annahme: Alle befragten Personen haben gültig gewählt.)
3%
3
2) Von einer Aussichtswarte sieht man einen Berggipfel, der sich im See spiegelt.
Von dieser Aussichtswarte, die sich 143 m über dem See (Seehöhe 542 m) befindet, misst man zur
Bergspitze einen Höhenwinkel von α = 14,35° und zur gespiegelten Spitze den Tiefenwinkel β = 18,70°.
Berechne die absolute Höhe des Berges.
h ≈ 1570 m
3) Laut Statistik vergessen 4 % aller Fahrgäste am Monatsersten eine neue Karte zu lösen.
a) Wie groß ist die Wahrscheinlichkeit, dass ein Kontrolleur bei 120 Fahrgästen
(1) genau 6; (2) mindestens 2 Personen ohne gültigen Fahrtausweis antrifft?
0,143; 0,955
b) Bei einer weiteren Kontrolle werden 400 Fahrgäste überprüft. Berechne die Wahrscheinlichkeit, dass
zwischen 6 und 26 Schwarzfahrer/innen (Grenzen jeweils miteingeschlossen) angetroffen werden.
Begründe, ob eine Näherung durch eine Normalverteilung vorgenommen werden darf, und vergleiche
die Ergebnisse der Berechnung mit einer Binomialverteilung mit jener bei der Näherung durch eine
Normalverteilung.
99,3%
5) Von einer Bakterienart sind zunächst 600 Bakterien pro ml vorhanden. Durch Beigabe einer bakterientötenden Substanz verringert sich die Anzahl innerhalb von 2 Tagen auf 450.
Formuliere ein geeignetes Abnahmegesetz für die Anzahl der vorhandenen Bakterien.
Wie viele sind noch nach 6 Tagen vorhanden?
253
Berechne, nach welchem Zeitraum die Anzahl der Bakterien pro ml auf 100 abgenommen hat.
12,5 d
Was kannst du über das mathematische Modell zur Ausrottung der Bakterien aussagen?
Entspricht es der Wirklichkeit?
6) Aus dem Graphen der Funktion f lässt sich die Temperaturänderung in °C in einem Reagenzglas während eines
chemischen Versuchs für die ersten 7 Minuten ablesen.
Kreuze die zutreffende(n) Aussage(n) an:
0 Im Intervall [3/6] ist die mittlere Änderungsrate 0°C/min.
0 Im Intervall [0,5/1,5] ist der Differenzenquotient
größer als 25°C/min
0 Der Differentialquotient zum Zeitpunkt t=3 ist etwa 10°C/min
0 Im Intervall [0/2] gibt es eine Zeitpunkt, an dem die momentane Änderungsrate 0°C/min beträgt.
0 Der Differenzenquotient ist im Intervall [2,t] mit 2<t<6 immer kleiner als 0°C/min.
1-3-4-5
7) Gegeben ist die Exponentialfunktion f mit f(x) = ex. Kreuze die zutreffende(n) Aussage(n) an.
0 Die Steigung der Tangente an der Stelle x=0 des Graphen hat den Wert 1.
0 Wird das Argument x um 1 erhöht, dann nimmt der Funktionswert um (e  1)  100 % zu.
0 Die Steigung der Tangente an der Stelle x=1 des Graphen hat den Wert e.
0 Wird das Argument x um 1 vermindert, dann nimmt der Funktionswert um 100/e % ab.
0 Der Graph von f hat an jeder Stelle eine positive Krümmung.
1-2-3-5
8) Die Funktion f mit f(x) = 100 . 2x stellt ein exponentielles Wachstum dar.
Wie verändert sich der Funktionswert, wenn x um 1 erhöht wird? Kreuze das Zutreffende an.
Wird x um 1 erhöht, so wird der Funktionswert f(x)
0 um 100 größer,
0 2+1 gleich +2 ist.
0 doppelt so groß,
weil
0 aus 100 dann 200 wird.
0 um 2 größer,
0 die 2er-Potenzen multipliziert werden, wenn man die
Hochzahlen addiert.
2c
9) Gegeben ist eine reelle Funktion f mit f(x) = 3x +2.
Kreuzen Sie die beiden Eigenschaften an, die auf die Funktion f zutreffen.
0 f(x+1) = f(x) + 3
0 f(x+1) = f(x) + 2
0 f(x+1) = 3 ∙ f(x)
0 f(x+1) = 2 ∙ f(x)
0 für
f ( x2 ) f ( x1 )
x2  x1
 3 für x1, x2 aus R und x1 ≠ x2
1-5
10) Es sind Funktionen f von folgendem Typus gegeben:
1.
2.
3.
4.
f(x) = k . x + d
f(x) = a . xz, zZ
f(x) = a . bx, a, b R+
f(x) = a . x½
In den Texten A, B, C, D sind funktionale Abhängigkeiten beschrieben. Suche zu jedem Text ein
passendes mathematisches Modell aus den angeführten Funktionstypen.
Text A: Die Anziehungskraft f(x) zwischen zwei Massen sinkt mit dem Quadrat ihrer Entfernung x.
Funktionstyp: 
Text B: Die Anzahl einer Insektenpopulation wächst täglich um p% der Anzahl des Vortages.
In x Tagen beträgt ihre Anzahl f(x).
Funktionstyp: 
Text C: Der Wert f(x) eines Gebrauchtwagen mit dem Neupreis N sinkt in x Jahren um m . x.
Funktionstyp: 
Text D: Die Seitenlänge eines Quadrates f(x) hängt vom Flächeninhalt x ab.
Funktionstyp: 
2-3-1-4
11) Gegeben sei der Graph der Polynomfunktion f.
Kreuze die beiden zutreffenden Aussagen an.
0 f (2)  0; f '(-2)  0; f (0)  4; f ''(0)  0; f ''(1)  0.
0 f (2)  0; f ''(-2)  0; f (0)  4; f '(0)  0; f '(1)  0.
0 f (2)  0; f ''(-2)  0; f '(0)  0; f ''(0)  0; f '(1)  0.
0 f (2)  0; f ''(-2)  0; f (0)  4; f ''(0)  0; f '(1)  0.
0 f (2)  0; f '(-2)  0; f (0)  4; f ''(0)  0; f '(1)  0.
1-3