PKLL-121

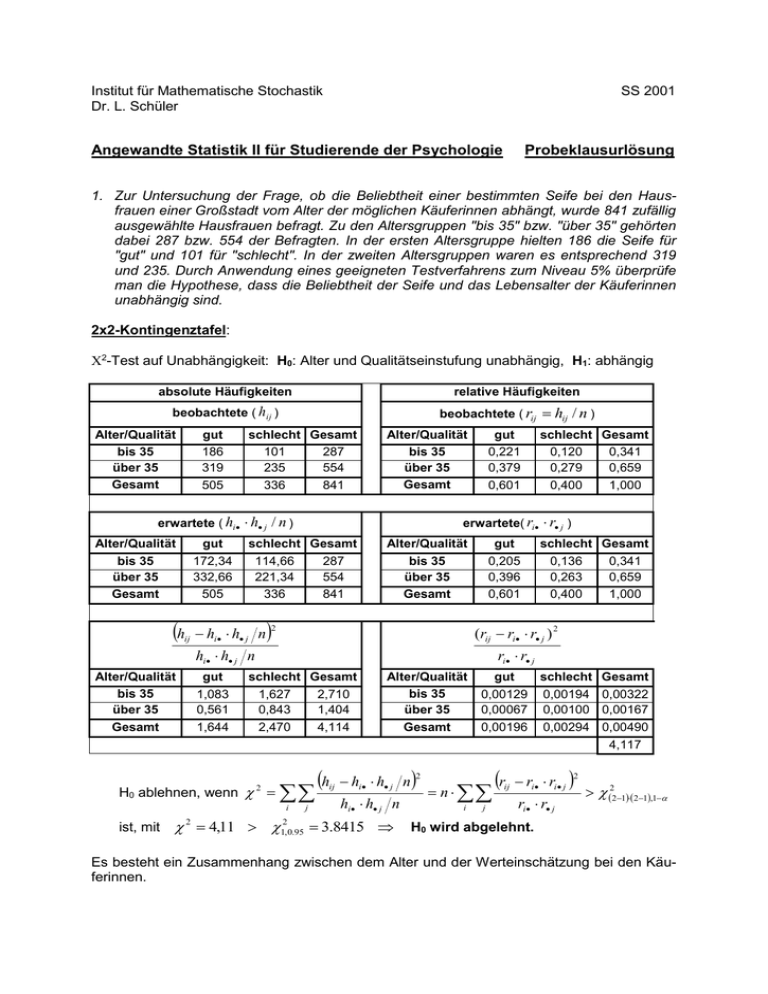
Institut für Mathematische Stochastik
Dr. L. Schüler
SS 2001
Angewandte Statistik II für Studierende der Psychologie
Probeklausurlösung
1. Zur Untersuchung der Frage, ob die Beliebtheit einer bestimmten Seife bei den Hausfrauen einer Großstadt vom Alter der möglichen Käuferinnen abhängt, wurde 841 zufällig
ausgewählte Hausfrauen befragt. Zu den Altersgruppen "bis 35" bzw. "über 35" gehörten
dabei 287 bzw. 554 der Befragten. In der ersten Altersgruppe hielten 186 die Seife für
"gut" und 101 für "schlecht". In der zweiten Altersgruppen waren es entsprechend 319
und 235. Durch Anwendung eines geeigneten Testverfahrens zum Niveau 5% überprüfe
man die Hypothese, dass die Beliebtheit der Seife und das Lebensalter der Käuferinnen
unabhängig sind.
2x2-Kontingenztafel:
2-Test auf Unabhängigkeit: H0: Alter und Qualitätseinstufung unabhängig, H1: abhängig
absolute Häufigkeiten
relative Häufigkeiten
beobachtete ( hij )
Alter/Qualität
bis 35
über 35
Gesamt
gut
186
319
505
beobachtete ( rij
schlecht Gesamt
101
287
235
554
336
841
Alter/Qualität
bis 35
über 35
Gesamt
erwartete ( hi   h j / n )
Alter/Qualität
bis 35
über 35
Gesamt
gut
172,34
332,66
505
h
schlecht Gesamt
114,66
287
221,34
554
336
841
Alter/Qualität
bis 35
über 35
Gesamt
 hi  h j n 
gut
0,205
0,396
0,601
gut
1,083
0,561
1,644
ri  r j
schlecht Gesamt
1,627
2,710
0,843
1,404
2,470
4,114
H0 ablehnen, wenn  
2

i
ist, mit
  4,11  
2
schlecht Gesamt
0,136
0,341
0,263
0,659
0,400
1,000
(rij  ri  r j ) 2
hi  h j n
Alter/Qualität
bis 35
über 35
Gesamt
schlecht Gesamt
0,120
0,341
0,279
0,659
0,400
1,000
erwartete( ri   r j )
2
ij
gut
0,221
0,379
0,601
 hij / n )
2
1, 0.95
j
h
ij
Alter/Qualität
bis 35
über 35
Gesamt
 hi  h j n 
2
hi  h j n
 3.8415 
gut
schlecht Gesamt
0,00129 0,00194 0,00322
0,00067 0,00100 0,00167
0,00196 0,00294 0,00490
4,117
 n  
i
j
r
ij
 ri  ri j 
2
ri  r j
  22121,1
H0 wird abgelehnt.
Es besteht ein Zusammenhang zwischen dem Alter und der Werteinschätzung bei den Käuferinnen.
2. Dem Hersteller eines Spülmittels wird von einer Verbraucherorganisation vorgeworfen, 3kg-Packungen in den Handel zu bringen, deren Inhalt wesentlich unter dem Nenngewicht
liegt. Die Organisation kauft 31 Packungen und stellt jeweils deren Nettogewicht fest.
Dabei ergeben sich ein Stichprobenmittelwert x  2,89 kg und eine Stichprobenvarianz
von s 2  0,04 kg 2 . Geben Sie geeignete Hypothesen an, um signifikant (5%) nachweisen zu können, dass der Hersteller tatsächlich das Nenngewicht im Mittel unterschreitet.
Welchen Test dürfen Sie verwenden und zu welchem Ergebnis kommt er?
Einstichproben-t-Test (einseitig):
Test erlaubt, da n  31  30 . X  "Nettogewicht einer Packung", EX :  .
H0:   3
gegen
H1:   3
H0 wird abgelehnt, falls
t
x  0
2,89  3
 n
 31  3.062  t n 1,1  t 30, 0.95  1,697
s
0,2
Ho wird abgelehnt. Es ist auf dem Signifikanzniveau 5% nachgewiesen, dass das
Nenngewicht im Mittel unterschritten wird.
3. Es soll der Einfluss eines Aufputschmittels ("Red Bull" etc.) auf die Fahrtüchtigkeit überprüft werden. Dazu wird ein Simulator als Messinstrument genutzt. Hier können die Versuchspersonen Fehlerpunkte auf einer Skala von 0 bis 100 machen, wobei 100 Fehlerpunkte für den absolut fahruntauglichen Probanden stehen. Die Fehlerpunkte verteilen
sich normal. Sie gehen mit dem Simulator in eine Diskothek o.ä. und werben um 2 Gruppen freiwilliger TeilnehmerInnen. Sie finden jeweils 23 Freiwillige: Alle TeilnehmerInnen
in der ersten Gruppe haben nachweislich ein Mindestmaß an Aufputschmitteln konsumiert, alle TeilnehmerInnen der anderen Gruppe nicht (=Kontrollgruppe). Sie messen in
beiden Gruppen den Stichprobenmittelwert: x1  33.5 , x2  27,8 und die Stichprobenstandardabweichungen s1  5.1 und s2  4.8 .
Testen Sie, ob zwischen den beiden Gruppen ein Unterschied hinsichtlich der Fahrtüchtigkeit besteht. Wählen Sie als Signifikanzniveau 5%, geben Sie die Hypothesen an und
bestimmen die kritischen Werte und die Entscheidungsregel, indem Sie Varianzhomogenität voraussetzen.
Zweistichproben-t-Test für unabhängige Stichproben (zweiseitig):
H0: 1   2
gegen
H0 wird abgelehnt, falls t  t n1 n2 2;1a 2 gilt, mit
t
x1  x2
n1  n2

ˆ
n1  n2
ˆ 2 
und
ˆ 2 
23  1  5.12  23  1  4.8 2
H1: 1   2
n1  1  s12  n2  1  s 22
n1  n2  2
 24,525 , ˆ  4.95
23  23  2
33,5  27,8
23  23
t

 3,905 , t 44;0,975  2,015 ,
4,95
23  23
Ho wird abgelehnt. Die Fahrtüchtigkeit ist in beiden Gruppen signifikant verschieden.
4. Eine neue Lernmethode soll eingeführt werden. Um sie zu überprüfen, wurden 5 Personen (Gruppe 1) nach der neuen und 6 Personen (Gruppe 2) nach der alten Methode unterrichtet. Die Lernergebnisse wurden in einer Klausur überprüft. Es wurden folgende
Punktzahlen erzielt: Gruppe 1: 55, 54, 34, 43, 39; Gruppe 2: 41, 51, 32, 25, 24, 15.
Man teste mit Hilfe eines geeigneten statistischen Tests, ob beide Methoden zu signifikant unterschiedlichen Ergebnissen führen (Irrtumswahrscheinlichkeit 5%).
Wilcoxon-Rangsummentest für 2 unabhängige Stichproben (zweiseitig):
i
xi yi Rg xi  Rg  yi 
1
2
3
4
5
6
55 41
54 51
34 32
43 25
39 24
15
Summe
1
2
7
4
6
5
3
8
9
10
11
20
46
X i  "Punktzahl in 1. Gruppe (alte Methode)" , Median X i   M x
i  1,, nx
 5
Yi  "Punktzahl in 2. Gruppe (neue Methode)" , Median Yi   M y
i  1,, n
 6
H0: M x  M y
gegen
y
H1: M x  M y
Tx  20 , T y  46 , n  n x  n y  5  6  11
H0 wird abgelehnt, falls Tx  wnx ,n y ; 2 oder Tx  wnx ,n y ;1 2 gilt. Tabellen dieser Quantile
liegen nicht für   5% also 1.    0,975 vor, deshalb benutzen wir die Normalapproximation (eigentlich erst erlaubt, falls n x , n y  25 gilt).
wnx ,n y ; 
1
1
 n x n  1  z 
 n x n y n  1
2
12
1
1
5  12
5  6  12
 n x n  1  z / 2 
 n x n y n  1 
 z 0,975
 30  1,96  30
2
12
2
12
 30  10,74  19,26
wnx ,n y ; / 2 
wnx ,n y ;1 / 2 
5  12
5  6  12
 z 0,975
 30  10,74  40,74
2
12
Ho wird nicht abgelehnt.
Ein Unterschied konnte nicht auf dem erforderlichen Niveau nachgewiesen werden.
5. Bei sechs gesunden Männern wurde der systolische Blutdruck mit dem Ziel gemessen,
Zusammenhänge zwischen Blutdruck und Lebensalter zu erkunden. Die Ergebnisse der
Messung sind in der folgender Tabelle dargestellt:
Alter
Blutdruck
20
125
25
130
35
155
45
145
55
165
60
180
Der empirische Korrelationskoeffizent zwischen dem Alter der Männer und dem bei ihnen
gemessenen Blutdruck ergibt sich zu rxy  0.93 . Was sagt dieser Wert aus? Testen Sie,
ob der Korrelationskoeffizient   X , Y  signifikant ( a  10%) von 0 verschieden ist.
X=Alter
20
25
35
45
55
60
240
Y=Druck
125
130
155
145
165
180
900
rxy 
x2
y2
xy
400 15625 2500
625 16900 3250
1225 24025 5425
2025 21025 6525
3025 27225 9075
3600 32400 10800
10900 137200 37575
1  n

  xi y i  n  x  y 
n  1  i 1

s x2  s y2
1  n 2
1  n 2


  xi  n  x 2  und s y2 
  yi  n  y 2 
n  1  i 1
n  1  i 1


240
900
1
x
 40 , y 
 150 , s x2  10900  6  40 2   260 ,
6
6
5
1
37575  6  40  150 315
1
2
2
5
s x  137200  6  150   440 , rxy 

 0,93
5
338,23
260  440
mit
s x2 
Starke positive Korrelation (lineare Steigerung des Blutdrucks mit dem Alter).
Test: H0:   0
T
rxy n  2
1  rxy2

gegen
0,93  6  2
H0 wird abgelehnt, falls
1  0.932

H1:   0
0.93  2
0.1351
 5.06
T  t n2;1 2  t 4;0.95  2,132 ist.
Ho wird abgelehnt. Der Korrelationskoeffizient ist signifikant von 0 verschieden (Blutdruck und Alter sind nicht unabhängig)
Der Test für die Steigung der Regressionsgeraden ist identisch. Ihre Steigung ist signifikant von Null verschieden.
6. Es soll gezeigt werden, dass die Reaktionszeit im Straßenverkehr durch eine neue Trainingsmethode verkürzt werden kann. Dazu wurden sechs Testpersonen (TP1-6) nach
der neuen Methode trainiert. Jeweils vor und nach dem Training wurde die Reaktionszeit
an einem Fahrsimulator gemessen. Die gemessenen Reaktionszeiten (in s) sind in der
folgenden Tabelle angegeben. Es ist bekannt, dass solche Reaktionszeiten normalverteilt
sind. Kann man die obige Frage aufgrund der folgenden Daten positiv beantworten
( a  10%) ?
vor Training
nach Training
TP1
0,7
0,75
TP2
0,8
0,65
TP3
0,75
0,7
TP4
0,6
0,6
TP5
0,8
0,7
TP6
0,85
0.9
Zweistichproben-t-Test (einseitig, abhängige (gepaarte) Stichprobe)
H0:  x   y
gegen
H1:  x   y
X=vor Y=nach d=X-Y
0,70
0,80
0,75
0,60
0,80
0,85
d 
0,75
0,65
0,70
0,60
0,70
0,90
-0,05
0,15
0,05
0,00
0,10
-0,05
0,20
d2
0,0025
0,0225
0,0025
0,0000
0,0100
0,0025
0,0400
0,20 1
1  n 2
 1

 0.033 , s d2 
  d i  n  d 2   0,04  6  0,0332  0,0067
6
30
n  1  i 1
 5

T
d
0,033
 n
6  1,00
sd
0,0067
H0 wird abgelehnt, falls T  t n 1;1  t 5;0.9  1,476 ist.
H0 kann nicht abgelehnt werden.
Es ist nicht bewiesen, dass das Training die Reaktionszeit verbessert.

7. Innerhalb einer größeren Studie zur geistigen und psychischen Entwicklung von Kindern
sollten Acht-, Neun- und Zehnjährige ein kleines Puzzle in möglichst kurzer Zeit zusammensetzen. Folgende Tabelle zeigt die benötigten Zeiten von je fünf zufällig ausgewählten Kindern der entsprechenden Altersgruppen in Minuten:
Alter
8
9
10
Ergebnisse
15 9 7 9 12
6 7 13 6 9
6 10 5 6 8
Ist anhand des vorliegenden Materials ein signifikanter Unterschied zwischen den Altersgruppen festzustellen ( a  5%) ?
Einfaktorielle Varianzanalyse:
p  3 , n  n1  n2  n3  5 , N  15
Ergebn
i
\
x
Alter
j
8
9
1
15
6
2
9
7
3
7
13
4
9
6
5
12
9
Gesamt 52 41
Mittel
10,4 8,2
x1 
10
6
10
5
6
8
35
7,0
i
Gesamt
1
2
3
4
5
Gesamt
128,00
8,53
52
 10,4 ,
5
j
\
 xj 
2
ij
8
9
10
Gesamt
21,16 4,84 1,00
1,96 1,44 9,00
11,56 23,04 4,00
1,96 4,84 1,00
2,56 0,64 1,00
39,20 34,80 16,00
90,00
x 2  8,2 , x3  7,0 , x 
128
8,53
15
SSerror   xij  x j   90,0
2

i
j
SStreat  n   x j  x   5  10,4  8,53  8,2  8,53  7,0  8,53
2
2
2
j
 5  5,94667  29,7333
SS treat  p  1
29,7333 2

 1,98
SS error n  1 p 
90,0 12
H0 wird abgelehnt, falls T  F p 1,n 1 p ;1  F2,12;0.95  3,885 ist.
T
H0 wird nicht abgelehnt.
Die Unterschiede zwischen den Altersgruppen sind nicht signifikant.
2
