Zusammenfassung Proportionalität
Werbung
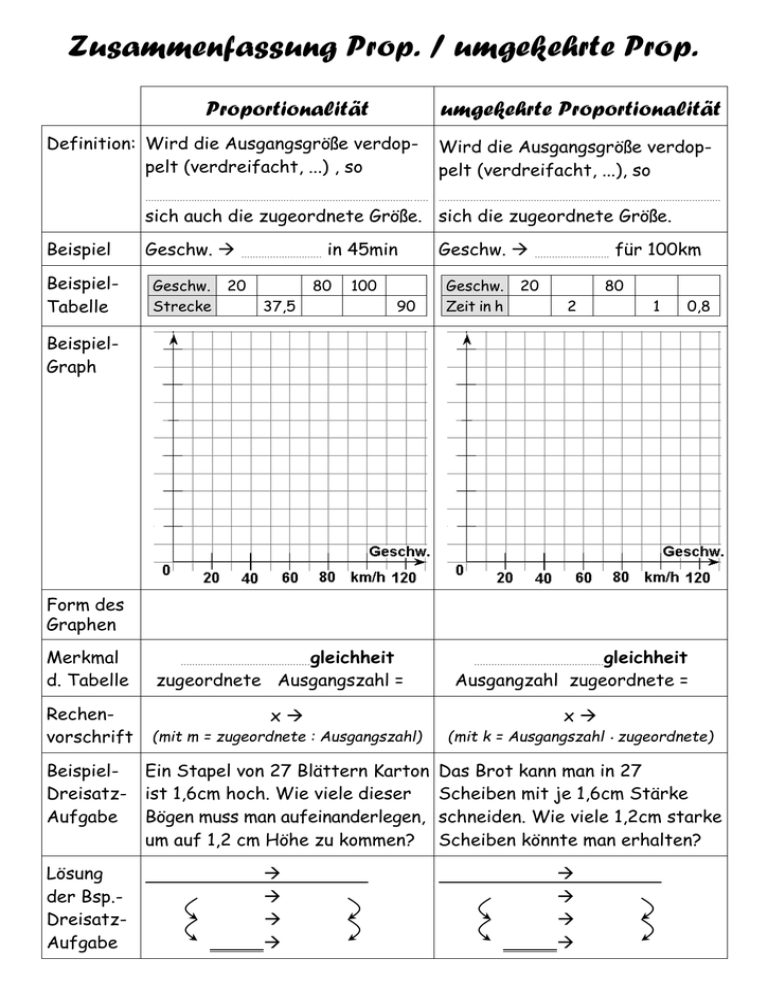
Zusammenfassung Prop. / umgekehrte Prop. Proportionalität umgekehrte Proportionalität Definition: Wird die Ausgangsgröße verdoppelt (verdreifacht, ...) , so Wird die Ausgangsgröße verdoppelt (verdreifacht, ...), so .................................................................................................. .................................................................................................. sich auch die zugeordnete Größe. sich die zugeordnete Größe. Beispiel BeispielTabelle Geschw. Geschw. Strecke ............................ 20 in 45min 80 100 37,5 90 Geschw. Geschw. Zeit in h .......................... 20 für 100km 80 2 1 0,8 BeispielGraph Form des Graphen Merkmal d. Tabelle Rechenvorschrift BeispielDreisatzAufgabe Lösung der Bsp.DreisatzAufgabe ............................................. gleichheit zugeordnete Ausgangszahl = x .............................................gleichheit Ausgangzahl zugeordnete = x (mit m = zugeordnete : Ausgangszahl) (mit k = Ausgangszahl zugeordnete) Ein Stapel von 27 Blättern Karton ist 1,6cm hoch. Wie viele dieser Bögen muss man aufeinanderlegen, um auf 1,2 cm Höhe zu kommen? Das Brot kann man in 27 Scheiben mit je 1,6cm Stärke schneiden. Wie viele 1,2cm starke Scheiben könnte man erhalten? 1,6cm 6,75 0,4cm 1,2cm . 1,6cm 6,75 0,4cm 1,2cm . Zusammenfassung Prop. / umgekehrte Prop. Proportionalität umgekehrte Proportionalität Definition: Wird die Ausgangsgröße verdoppelt (verdreifacht, ...) , so verdoppelt (verdreifacht, ...) sich auch die zugeordnete Größe. Wird die Ausgangsgröße verdoppelt (verdreifacht, ...), so halbiert (drittelt, ...) sich die zugeordnete Größe. Beispiel Geschw. Fahrzeit für 100km BeispielTabelle Geschw. Strecke in 45min Geschw. 20 Strecke 15 50 37,5 80 60 100 75 120 90 Geschw. Zeit in h 20 5 50 2 80 100 1,25 1 125 0,8 BeispielGraph Form des Graphen Gerade durch Ursprung Hyperbel Merkmal d. Tabelle Quotientengleichheit zugeordnete : Ausgangszahl = m Produktgleichheit Ausgangzahl zugeordnete = k Rechenvorschrift xmx xk:x (mit m = zugeordnete : Ausgangszahl) (mit k = Ausgangszahl zugeordnete) BeispielDreisatzAufgabe Ein Stapel von 27 Blättern Karton ist 1,6cm hoch. Wie viele dieser Bögen muss man aufeinanderlegen, um auf 1,2 cm Höhe zu kommen? Das Brot kann man in 27 Scheiben mit je 1,6cm Stärke schneiden. Wie viele 1,2cm starke Scheiben könnte man erhalten? Lösung der Bsp.DreisatzAufgabe Anzahl Bögen Höhe 27 1,6cm :4 6,75 0,4cm 3 20,25 1,2cm Anzahl Scheiben Stärke 27 1,6cm 4 108 0,4cm :3 36 1,2cm :4 3 :4 3